Расчет интерференционной картины от двух когерентных источников. Оптическая длина пути.
Свободные затухающие колебания пружинного маятника
Для пружинного маятника, совершающего малые гармонические колебания под действием упругой силы F = - kx, а еще на него действует сила трения
| F тр = − rV = − rx, | (7.15) |
где r - коэффициент сопротивления, ( - ) показывает, что направления силы трения и скорости противоположны.
| Тогда уравнение движения маятника будет иметь вид: | |
| mx = − kx − rx, | (7.16) |
| Вспомним, что ω 2о = k / m и обозначив r / m = 2 δ получаем | |
| x + 2 δ x +ω 02 = 0 , | (7.17) |
дифференциальное уравнение затухающих колебаний маятника, но его решение имеет вид:
| x = A 0 e −δ t | cos( ω t +ϕ ) , | (7.18) | ||||||||||||
| где ω = | ω 02 | − r 2 | . | |||||||||||
| 4m 2 | ||||||||||||||
| Добротность пружинного маятника: | ||||||||||||||
| Q = | π | = | π | = | π 2m | = | 2 π m | = | mk . | (7.19) | ||||
| λ | δ T | rT | r2 π | |||||||||||
| m k | r | |||||||||||||
| λ =δ T = 2 π r | 2 | = | π r. | (7.20) | ||||||||||
| 2mk | mk | |||||||||||||
Свободные затухающие колебания в электрическом колебательном контуре
Если в колебательном контуре R ≠ 0 , то дифференциальное уравнение свободного затухающего колебания заряда в контуре имеет вид:
| q + q | R | + | q | = 0 , | (7.21) | ||||||||||
| CL | |||||||||||||||
| L | |||||||||||||||
| сравнивая с уравнением x + 2 δ x + ω 2о = 0 имеем
| |||||||||||||||
| δ = | R | , | (7.22) | ||||||||||||
| 2L | |||||||||||||||
| ω 02 = | 1 | . | (7.23) | ||||||||||||
| LC | |||||||||||||||
| Решением (7.21) является функция: | |||||||||||||||
| q = q max e −δ t cos( ω t +ϕ ) , | (7.24) | ||||||||||||||
| a | |||||||||||||||
| ω = ω 02 −δ 2 | = | 1 | − | R 2 | , | (7.25) | |||||||||
| LC | 4L 2 | ||||||||||||||
ω<ωо.
1
Если R = 0 , то ω =ωо =  LC Логарифмический декремент определяется так:
LC Логарифмический декремент определяется так:
| λ = | 2 π R LC =π R | C , | (7.26) | |||||
| 2L | L | |||||||
| а добротность | ||||||||
| Q = | π | = | π | = | 1 | L . | (7.27) | |
| λ | π R | C | R | C | ||||
| L | ||||||||
C ростом δ растет и период затухающих колебаний и приδ =ωо Т = =∞ , колеблющаяся величина асимптотически приближается к 0, когда t→ ∞. Процесс перестает быть периодическим.
Оказывается возможно поддерживать колебания незатухающими. Для этого необходимо восполнять потери энергии в реальной колебательной системе. Особенно широко применяются автоколебания.
|
|
|
Автоколебания - незатухающие колебания, поддерживаемые в колебательной системе за счет постоянного внешнего источника энергии, а свойства этих колебаний определяются самой системой.
Автоколебательная система сама управляет внешними воздействиями, обеспечивая согласованность поступления энергии нужными порциями в нужный момент. Примером автоколебательной системы могут служить часы. Механизм подталкивает маятник в такт с его колебаниями. Энергия, передаваемая при этом берется либо за счет раскручивающийся пружины, либо за счет опускающегося груза. Автоколебательными системами являются также ДВС, паровые турбины, ламповый генератор.
7.
тобы в реальной колебательной системе получить незатухающие колебания, надо компенсировать потери энергии. Такая компенсация возможна с помощью какого-либо периодически действующего фактора X(t), изменяющего по гармоническому закону:
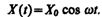
Если рассматривать механические колебания, то роль X(t) играет внешняя вынуждающая сила
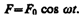 (147.1)
(147.1)
С учетом (147.1) закон движения для пружинного маятника (146.9) запишется в виде
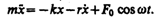
Используя (142.2) и (146.10), придем к уравнению
|
|
|
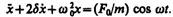 (147.2)
(147.2)
Если рассматривать электрический колебательный контур, то роль X(t) играет подводимая к контуру внешняя периодически изменяющаяся по гармоническому закону э.д.с. или переменное напряжение
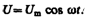 (147.3)
(147.3)
Тогда уравнение (143.2) с учетом (147.3) можно записать в виде
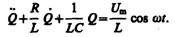
Используя (143.4) и (146.11), придем к уравнению
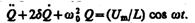 (147.4)
(147.4)
Колебания, возникающие под действием внешней периодически изменяющейся силы или внешней периодически изменяющейся э.д.с., называются соответственно вынужденными механическими и вынужденными электромагнитными колебаниями.
Уравнения (147.2) и (147.4) можно свести к линейному неоднородному дифференциальному уравнению
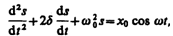 (147.5)
(147.5)
применяя впоследствии его решение для вынужденных колебаний конкретной физической природы (x0 в случае механических колебаний равно F0/ m , в случае электромагнитных — Um/L).
Решение уравнения (147.5) равно сумме общего решения (146.5) однородного уравнения (146.1) и частного решения неоднородного уравнения. Частное решение найдем в комплексной форме. Заменим правую часть уравнения (147.5) на комплексную величину х0 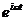 :
:
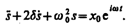 (147.6)
(147.6)
Частное решение этого уравнения будем искать в виде
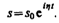
Подставляя выражение для s и его производных 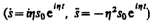 в уравнение (147.6), получаем
в уравнение (147.6), получаем
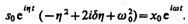 (147.7)
(147.7)
|
|
|
Так как это равенство должно быть справедливым для всех моментов времени, то время t из него должно исключаться. Отсюда следует, что h = w . Учитывая это, из уравнения (147.7) найдем величину s0 и умножим ее числитель и знаменатель на 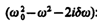
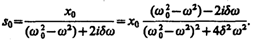
Это комплексное число удобно представить в экспоненциальной форме:
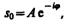
где
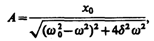 (147.8)
(147.8)
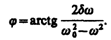 (147.9)
(147.9)
Следовательно, решение уравнения (147.6) в комплексной форме примет вид
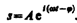
Его вещественная часть, являющаяся решением уравнения (147.5), равна
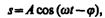 (147.10)
(147.10)
где А и j задаются соответственно формулами (147.8) и (147.9).
Таким образом, частное решение неоднородного уравнения (147.5) имеет вид
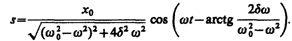 (147.11)
(147.11)
Решение уравнения (147.5) равно сумме общего решения однородного уравнения
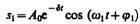 (147.12)
(147.12)
(см. (146.5)) и частного решения (147.11). Слагаемое (147.12) играет существенную роль только в начальной стадии процесса (при установлении колебаний) до тех пор, пока амплитуда вынужденных колебаний не достигнет значения, определяемого равенством (147.8). Графически вынужденные колебания представлены на рис. 209. Следовательно, в установившемся режиме вынужденные колебания происходят с частотой w и являются гармоническими; амплитуда и фаза колебаний, определяемые выражениями (147.8) и (147.9), также зависят от w .

Запишем формулы (147.10), (147.8) и (147.9) для электромагнитных колебаний, учитывая, что 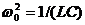 (см. (143.4)) и
(см. (143.4)) и 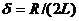 (см. (146.11)):
(см. (146.11)):
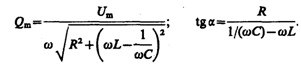 (147.13)
(147.13)
Продифференцировав Q = Qmcos(w t – a) по t , найдем силу тока в контуре при установившихся колебаниях:
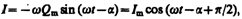 (147.14)
(147.14)
где
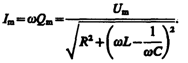 (147.15)
(147.15)
Выражение (147.14) может быть записано в виде
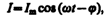
где j=a – p/2 — сдвиг по фазе между током и приложенным напряжением (см. (147.3)). В соответствии с выражением (147.13)
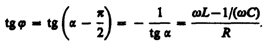 (147.16)
(147.16)
8.
Колебания, возбужденные в какой-либо точке среды (твердой, жидкой или газообразной), распространяются в ней с конечной скоростью, зависящей от свойств среды, передаваясь от одной точки среды к другой. Чем дальше расположена частица среды от источника колебаний, тем позднее она начнет колебаться. Иначе говоря, фазы колебаний частиц среды и источника тем больше отличаются друг от друга, чем больше это расстояние. При изучении распространения колебаний не учитывается дискретное (молекулярное) строение среды и среда рассматривается как сплошная, т. е. непрерывно распределенная в пространстве и обладающая упругими свойствами.
Процесс распространения колебаний в сплошной среде называется волновым процессом (или волной). При распространении волны частицы среды не движутся вместе с волной, а колеблются около своих положений равновесия. Вместе с волной от частицы к частице среды передаются лишь состояние колебательного движения и его энергия. Поэтому основным свойством всех волн, независимо от их природы, является перенос энергии без переноса вещества.
Среди разнообразных волн, встречающихся в природе и технике, выделяются следующие их типы: волны на поверхности жидкости, упругие и электромагнитные волны. Упругими (или механическими) волнами называются механические возмущения, распространяющиеся в упругой среде. Упругие волны бывают продольные и поперечные. В продольных волнах частицы среды колеблются в направлении распространения волны, в поперечных — в плоскостях, перпендикулярных направлению распространения волны.
Продольные волны могут возбуждаться в средах, в которых возникают упругие силы при деформации сжатия и растяжения, т. е. твердых, жидких и газообразных телах. Поперечные волны могут возбуждаться в среде, в которой возникают упругие силы при деформации сдвига, т. е. в твердых телах; в жидкостях и газах возникают только продольные волны, а в твердых телах — как продольные, так и поперечные.
Упругая волна называется гармонической, если соответствующие ей колебания частиц среды являются гармоническими. На рис. 220 представлена гармоническая поперечная волна, распространяющаяся со скоростью v вдоль оси х, т. е. приведена зависимость между смещением x частиц среды, участвующих в волновом процессе, и расстоянием х этих частиц (например, частицы В) от источника колебаний О для какого-то фиксированного момента времени t. Приведенный график функции x(x , t)похож на график гармонического колебания, однако они различны по существу. График волны дает зависимость смещения всех частиц среды от расстояния до источника колебаний в данный момент времени, а график колебаний — зависимость смещения данной частицы от времени.
Расстояние между ближайшими частицами, колеблющимися в одинаковой фазе, называется длиной волны l (рис. 220). Длина волны равна тому расстоянию, на которое распространяется определенная фаза колебания за период, т. е.
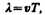
или, учитывая, что T= 1/n, где n — частота колебаний,
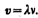

Если рассмотреть волновой процесс подробнее, то ясно, что колеблются не только частицы, расположенные вдоль оси х, а колеблется совокупность частиц, расположенных в некотором объеме, т. е. волна, распространяясь от источника колебаний, охватывает все новые и новые области пространства. Геометрическое место точек, до которых доходят колебания к моменту времени t, называется волновым фронтом. Геометрическое место точек, колеблющихся в одинаковой фазе, называется волновой поверхностью. Волновых поверхностей можно провести бесчисленное множество, а волновой фронт в каждый момент времени — один. Волновой фронт также является волновой поверхностью. Волновые поверхности могут быть любой формы, а в простейшем случае они представляют собой совокупность плоскостей, параллельных друг другу, или совокупность концентрических сфер. Соответственно волна называется плоской или сферической.
9.
Уравнение плоской одномерной синусоидальной волны:
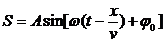
(Вместо синуса можно написать косинус.) Это уравнение отличается от уравнения синусоидальных колебаний тем, что колеблющая величина S зависит не только от времени, но и от координаты. Это и понятно: вместо одного маятника мы имеем множество связанных маятников - частиц среды. v - скорость распространения волны, А - амплитуда волны, аргумент синуса - фаза волны, j0 - начальная фаза колебаний в точке х = 0,w - частота (циклическая) волны.
Расстояние, на которое распространяется волна за время, равное периоду колебаний, называется ДЛИНОЙ ВОЛНЫ l = nT.
ВОЛНОВОЕ ЧИСЛО k:
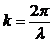
С помощью введенного волнового числа уравнение волны запишется:
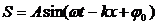
Если мы рассматриваем не одномерную волну, удобно наряду с волновым числом ввести ВОЛНОВОЙ ВЕКТОР k, модуль которого равен волновому числу, а направление совпадает с направлением луча (направлением распространения волны). В векторном виде уравнение волны будет выглядеть так:
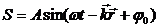
здесь r - радиус вектор точки пространства; j0 - начальная фаза колебаний в начале координат.
Уравнение сферической волны отличается тем, что амплитуда волны убывает с расстоянием от источника:
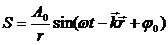
A0 = const по смыслу формулы есть амплитуда волны на единичном расстоянии от источника.
Уравнение волны в дифференциальной форме обычно называют волновым уравнением; вид этого уравнения следующий:
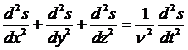 или
или 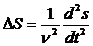
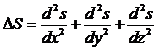
Уравнение синусоидальной волны является решением волнового уравнения (можно проверить подстановкой). Общее же решение волнового уравнения следующее:
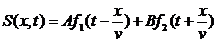
Здесь А и В - произвольные константы, а f 1 и f2 - произвольные дважды дифференцируемые функции. Первое слагаемое описывает волну, распространяющуюся слева направо, второе - встречную волну.
Фазовая скорость – это скорость распространения фазы волны.
Зафиксируем какое-либо значение фазы волны и проследим, с какой скоростью фаза будет перемещаться вдоль оси x.
.
Это уравнение дает связь между t и тем значением x, где зафиксированное значение фазы будет в данный момент времени. Следовательно, – это есть скорость перемещения данной фазы.Т.к., поэтому . Возьмем производную по времени от обеих частей равенства: . Отсюда получим выражение для фазовой скорости:
| . | (5.3.1) |
Итак, скорость распространения фазы есть скорость распространения волны. Т.е. υ в уравнении волны есть фазовая скорость. Для синусоидальной волны скорость переноса энергии равна фазовой скорости. Но синусоидальная волна не несет никакой информации, любой сигнал – это модулированная волна, т.е. несинусоидальная (негармоническая).
При решении некоторых задач получается, что фазовая скорость больше скорости света. Здесь нет парадокса, так как скорость перемещения фазы – это не скорость передачи (распространения) энергии, которая не может распространяться со скоростью большей, чем скорость света с.
10.
Особым случаем интерференции являются стоячие волны – это волны, образующиеся при наложении двух волн одинаковой частоты и амплитуды, распространяющихся навстречу друг другу.
Такой случай можно реализовать, заставив бегущую волну отразиться от преграды (рис. 24).
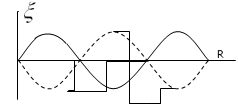
Рис. 24
Уравнения падающей и отражённой волн имеют вид:
ξ1(r,t)=A·cos[ω(t-r/υ)]
ξ2(r,t)=A·cos[ω(t+r/υ)]
Сложив эти уравнения, используя тригонометрические преобразования, получаем уравнение стоячей волны:
ξ=ξ1+ξ2=|2A·cos(2πr/λ)|·cosωt (119)
где амплитуда стоячей волны:
Aст.=|2A·cos(2πr/λ)| (120)
Из выражения (120) видно, что амплитуда стоячей волны:
0 ≤ Aст. ≤ 2A (121)
Точки, в которых амплитуды бегущей и отражённой волны складываются, называются пучностями (Aп=2A).
Точки, в которых амплитуда равна нулю, называются узлами (Aуз=0). Эти точки колебаний не совершают.
Пучность образуется в тех точках, где колебания бегущей и отражённой волн происходят в одинаковой фазе, т.е. 2πr/λ=±πk (k=0,1,2,...). Следовательно, координаты пучностей:
rn=±λk/2 (k=0,1,2,...) (122)
Узлы образуются там, где колебания происходят в противофазах, т.е. 2πr/λ=±(k+0.5)π (k=0,1,2,...). Следовательно, координаты узлов:
rуз.=±(k+0.5)·λ/2 (k=0,1,2,...) (123)
Длиной стоячей волны называется расстояние между пучностями или узлами:
λст.=Δrn=λ/2(k+1)-kλ/2=λ/2
Таким образом, длина стоячей волны равна половине длины складываемых волн:
λст.=λ/2 (124)
Стоячая волна не переносит энергии, т.к. энергия переносится в равных количествах бегущей и отражённой волнами.
11.
Явление интерференции свидетельствует о том, что свет — это волна.
Интерференцией световых волн называется сложение двух когерентных волн, вследствие которого наблюдается усиление или ослабление результирующих световых колебаний в различных точках пространства.
Интерференцию света можно объяснить, рассматривая интерференцию волн. Необходимым условием интерференции волн является их когерентность, т. е. согласованное протекание во времени и пространстве нескольких колебательных или волновых процессов. Этому условию удовлетворяют монохроматические волны — неограниченные в пространстве волны одной определенной и строго постоянной частоты. Taк как ни один реальный источник не дает строго монохроматического света, то волны, излучаемые любыми независимыми источниками света, всегда некогерентны. Поэтому на опыте не наблюдается интерференция света от независимых источников, например от двух электрических лампочек.
Понять физическую причину немонохроматичности, а следовательно, и некогерентности волн, испускаемых двумя независимыми источниками света, можно исходя из самого механизма испускания света атомами. В двух самостоятельных источниках света атомы излучают независимо друг от друга. В каждом из таких атомов процесс излучения конечен и длится очень короткое время (t » 10–8с). За это время возбужденный атом возвращается в нормальное состояние и излучение им света прекращается. Возбудившись вновь, атом снова начинает испускать световые волны, но уже с новой начальной фазой. Так как разность фаз между излучением двух таких независимых атомов изменяется при каждом новом акте испускания, то волны, спонтанно излучаемые атомами любого источника света, некогерентны. Таким образом, волны, испускаемые атомами, лишь в течение интервала времени 10–8с имеют приблизительно постоянные амплитуду и фазу колебаний, тогда как за больший промежуток времени и амплитуда, и фаза изменяются. Прерывистое излучение света атомами в виде отдельных коротких импульсов называется волновым цугом.
Описанная модель испускания света справедлива и для любого макроскопического источника, так как атомы светящегося тела излучают свет такженезависимо друг от друга. Это означает, что начальные фазы соответствующих им волновых цугов не связаны между собой. Помимо этого, даже для одного и того же атома начальные фазы разных цугов отличаются для двух последующих актов излучения. Следовательно, свет, испускаемый макроскопическим источником, некогерентен.
Любой немонохроматический свет можно представить в виде совокупности сменяющих друг друга независимых гармонических цугов. Средняя продолжительность одного цуга tког называется временем когерентности. Когерентность существует только в пределах одного цуга, и время когерентности не может превышать время излучения, т. е. tког < t. Прибор обнаружит четкую интерференционную картину лишь тогда, когда время разрешения прибора значительно меньше времени когерентности накладываемых световых волн.
Если волна распространяется в однородной среде, то фаза колебаний в определенной точке пространства сохраняется только в течение времени когерентности tког. За это время волна распространяется в вакууме на расстояние lког =с tког, называемое длиной когерентности (или длиной цуга). Таким образом, длина когерентности есть расстояние, при прохождении которого две или несколько волн утрачивают когерентность. Отсюда следует, что наблюдение интерференции света возможно лишь при оптических разностях хода, меньших длины когерентности для используемого источника света.
Чем ближе волна к монохроматической, тем меньше ширина Dw спектра ее частот и, как можно показать, больше ее время когерентности tког, а следовательно, и длина когерентности lког. Когерентность колебаний, которые совершаются в одной и той же точке пространства, определяемая степенью монохроматичности волн, называется временнóй когерентностью.
Наряду с временнóй когерентностью для описания когерентных свойств волн в плоскости, перпендикулярной направлению их распространения, вводится понятие пространственной когерентности. Два источника, размеры и взаимное расположение которых позволяют (при необходимой степени монохроматичности света) наблюдать интерференцию, называются пространственно-когерентными. Радиусом когерентности (или длиной пространственной когерентности) называется максимальное поперечное направлению распространения волны расстояние, на котором возможно проявление интерференции. Таким образом, пространственная когерентность определяется радиусом когерентности. Радиус когерентности
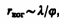
где l — длина волны света, j — угловой размер источника. Так, минимально возможный радиус когерентности для солнечных лучей (при угловом размере Солнца на Земле j » 10–2 рад и l » 0,5 мкм) составляет » 0,05 мм. При таком малом радиусе когерентности невозможно непосредственно наблюдать интерференцию солнечных лучей, поскольку разрешающая способность человеческого глаза на расстоянии наилучшего зрения составляет лишь 0,1 мм. Отметим, что первое наблюдение интерференции провел в 1802 г. Т. Юнг именно с солнечным светом, для чего он предварительно пропускал солнечные лучи через очень малое отверстие в непрозрачном экране (при этом на несколько порядков уменьшался угловой размер источника света и тем самым резко увеличивался радиус когерентности (или длина пространственной когерентности)).
12.
Рассмотрим более подробно основные свойства интерференционной картины, создаваемой двумя источниками электромагнитных волн одинаковой интенсивности и наблюдаемой на плоском экране, расположенным на расстоянии l от плоскости расположения от источников. В качестве таких источников могут мыслиться, например две бесконечно-узкие, параллельные друг - другу щели или два отверстия бесконечно малого диаметра, расстояние между которыми d<<l , прорезанные в плоском непрозрачном экране. Пусть источники электромагнитных волн располагаются в однородной среде с показателем преломления.
Область, в которой волны источников перекрываются, называется полем интерференции. В поле интерференции имеются места, где волны источников будут складываться в фазе. В этих местах будут отмечаться максимумы интенсивности электромагнитного поля. Там же, где волны будут складываться в противофазе - минимальная интенсивность . Если в поле интерференции поместить непрозрачный экран, то будет наблюдается чередование светлых и тёмных полос (рис. 4.3a), представляющие собой интерференционную
картину. 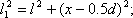
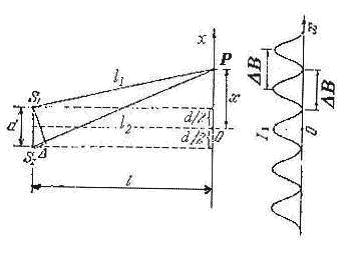
Расчет интерференционной картины от двух когерентных источников. Оптическая длина пути.
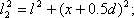 l1 и l2расстояния, проходимые волнами соответственно от первого и второго источников до точки наблюдения.
l1 и l2расстояния, проходимые волнами соответственно от первого и второго источников до точки наблюдения.
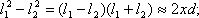
Из (l1 + l2)~2 l следует что: 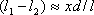
Максимум интерференционной картины будет наблюдаться при условии синфазного сложения колебаний волн источников. синфазное сложение колебаний имеет место при условии кратности оптической разности хода целому числу длин волны в среде. Порядком интерференционного максимума называют его номер, отсчитываемый от центрального, которому соответствует центр интерференционной картины , где складываются волны от источников, проходящие одинаковый путь. Найти положения минимумов интерференционной картины двух источников можно если положить оптическую разность хода кратной нечётному числу полуволн. Положения соседних интерференционных максимумов и минимумов находятся на одинаковом расстоянии друг от друга и не зависят от того, насколько эти максимумы удалены от центра интерференционной картины.
Оптической длиной пути в однородной среде называется произведение расстояния, пройденного светом в среде с показателем преломления n, на показатель преломления: l = nS Для неоднородной среды необходимо разбить геометрическую длину на столь малые промежутки, что можно было бы считать на этом промежутке показатель преломления постоянным: dl = nds. Полная оптическая длина пути находится интегрированием: 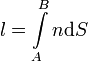
13.
Интерференционные полосы равного наклона. При освещении тонкой пленки происходит наложение волн от одного и того же источника, отразившихся от передней и задней поверхностей пленки. При этом может возникнуть интерференция света. Если свет белый, то интерференционные полосы окрашены. Интерференцию в пленках можно наблюдать на стенках мыльных пузырей, на тонких пленках масла или нефти, плавающих на поверхности воды, на пленках, возникающих на поверхности металлов или зеркала.
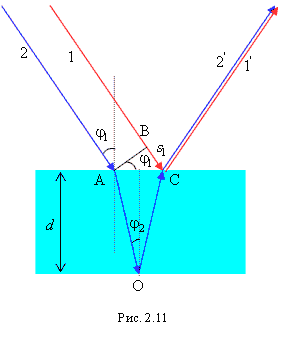 Рассмотрим сначала плоскопараллельную пластинку толщины
Рассмотрим сначала плоскопараллельную пластинку толщины 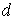 с показателем преломления
с показателем преломления 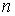 (рис. 2.11). Пусть на пластинку падает плоская световая волна, которую можно рассматривать как параллельный пучок лучей. Пластинка отбрасывает вверх два параллельных пучка света, один из которых
(рис. 2.11). Пусть на пластинку падает плоская световая волна, которую можно рассматривать как параллельный пучок лучей. Пластинка отбрасывает вверх два параллельных пучка света, один из которых 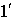 образовался за счет отражения от верхней поверхности пластинки, второй
образовался за счет отражения от верхней поверхности пластинки, второй 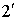 – вследствие отражения от нижней поверхности. Каждый из этих пучков представлен на рис. 2.11 только одним лучом.
– вследствие отражения от нижней поверхности. Каждый из этих пучков представлен на рис. 2.11 только одним лучом.
При входе в пластинку и при выходе из нее пучок 2 претерпевает преломление. Кроме двух пучков 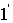 и
и 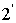 , пластинка отбрасывает вверх пучки, возникающие в результате трех-, пяти- и т.д. кратного отражения от поверхностей пластинки. Однако ввиду малой интенсивности их можно не принимать во внимание.
, пластинка отбрасывает вверх пучки, возникающие в результате трех-, пяти- и т.д. кратного отражения от поверхностей пластинки. Однако ввиду малой интенсивности их можно не принимать во внимание.
Рассмотрим интерференцию лучей, отраженных от пластинки. Поскольку на пластинку падает плоская волна, то фронт этой волны представляет собой плоскость, перпендикулярную лучам 1 и 2. На рис. 2.11 прямая ВС представляет собой сечение волнового фронта плоскостью рисунка. Оптическая разность хода, приобретаемая лучами 1 и 2 до того, как они сойдутся в точке С, будет
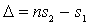 , ,
| (2.13) |
где 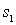 – длина отрезка ВС, а
– длина отрезка ВС, а 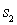 – суммарная длина отрезков АО и ОС. Показатель преломления среды, окружающей пластинку, полагаем равным единице. Из рис. 2.11 видно, что
– суммарная длина отрезков АО и ОС. Показатель преломления среды, окружающей пластинку, полагаем равным единице. Из рис. 2.11 видно, что 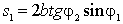 ,
, 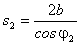 . Подстановка этих выражений в (2.13) дает
. Подстановка этих выражений в (2.13) дает 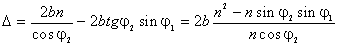 . Воспользуемся законом преломления света:
. Воспользуемся законом преломления света: 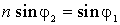 ; и учтем, что
; и учтем, что 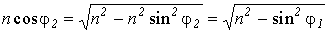 , тогда для разности хода получим следующее выражение:
, тогда для разности хода получим следующее выражение: 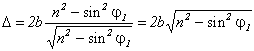 .
.
При вычислении разности фаз между колебаниями в лучах  и
и 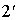 нужно, кроме оптической разности хода D, учесть возможность изменения фазы при отражении в точке С. В точке С отражение волны происходит от границы раздела среды оптически менее плотной со средой оптически более плотной. Поэтому фаза волны претерпевает изменение на p. В точке
нужно, кроме оптической разности хода D, учесть возможность изменения фазы при отражении в точке С. В точке С отражение волны происходит от границы раздела среды оптически менее плотной со средой оптически более плотной. Поэтому фаза волны претерпевает изменение на p. В точке 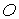 отражение происходит от границы раздела среды оптически более плотной со средой оптически менее плотной, и скачка фазы в этом случае не происходит. Качественно это можно представить себе следующим образом. Если толщину пластинки устремить к нулю, то полученная нами формула для оптической разности хода дает
отражение происходит от границы раздела среды оптически более плотной со средой оптически менее плотной, и скачка фазы в этом случае не происходит. Качественно это можно представить себе следующим образом. Если толщину пластинки устремить к нулю, то полученная нами формула для оптической разности хода дает 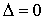 . Поэтому при наложении лучей
. Поэтому при наложении лучей  и
и 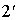 должно происходить усиление колебаний. Но это невозможно, так как бесконечно тонкая пластинка вообще не может оказывать влияния на распространение света. Поэтому волны, отраженные от передней и задней поверхности пластинки, должны при интерференции гасить друг друга. Их фазы должны быть противоположны, то есть оптическая разность хода D при d→0 должна стремиться к
должно происходить усиление колебаний. Но это невозможно, так как бесконечно тонкая пластинка вообще не может оказывать влияния на распространение света. Поэтому волны, отраженные от передней и задней поверхности пластинки, должны при интерференции гасить друг друга. Их фазы должны быть противоположны, то есть оптическая разность хода D при d→0 должна стремиться к 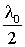 . Поэтому к прежнему выражению для D нужно прибавить или вычесть
. Поэтому к прежнему выражению для D нужно прибавить или вычесть 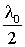 , где λ0 – длина волны в вакууме. В результате получается:
, где λ0 – длина волны в вакууме. В результате получается:
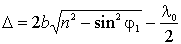 . .
| (2.14) |
Итак, при падении на пластинку плоской волны образуются две отраженные волны, разность хода которых определяется формулой (2.14). Эти волны могут интерферировать, если оптическая разность хода не превышает длину когерентности. Последнее требование для солнечного излучения приводит к тому, что интерференция при освещении пластинки наблюдается только в том случае, если толщина пластинки не превышает нескольких сотых миллиметра.
14.
Дата добавления: 2020-04-08; просмотров: 230; Мы поможем в написании вашей работы! |

Мы поможем в написании ваших работ!
