II способ нахождения наименьшего значения данной функции (с помощью производной)
Исследуем функцию 
с помощью производной на экстремум.
1. 
. Функция непрерывна на всей области определения.
2. 
.
3. Найдем критические точки: 
, 
. (это запись не раскрывает все процедуры проверки определения критических точек)
4. Теорема Дарбу. Точки, в которых производная функции равна 0 или не существует, делят область определения функции на интервалы, внутри которых производная сохраняет знак. Составим таблицу монотонности:
| 
| 
| |
| __ | 0 | + |
| 
| ||
|
Определим знаки производной на каждом интервале и характер монотонности функции.
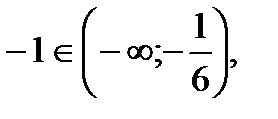
По достаточному признаку убывания функции, на данном промежутке функция убывает.
По достаточному признаку возрастания функции, на данном промежутке функция возрастает. Таким образом, по признаку минимума функции, т.к. производная в точке 
меняет знак с минуса на плюс, то 
- точка минимума. Итак, наша функция принимает наименьшее значение в точке .
Ответ: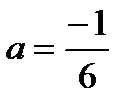 
| Распределение баллов | Критерии задания № 6 |
| 20 баллов | Полное и верное решение. |
| 17 – 19 баллов | Верное решение с недочётами, в целом не влияющее на решение (запись решения, не полная аргументация решения, не рациональное решение). |
| 14 – 16 баллов | Решение в целом выполнено, верно, но неполно или содержит непринципиальные ошибки. Правильно найден определённый интеграл, но не рассмотрено свойство квадратичной функции, не сделан вывод о наименьшем значении функции. Или в исследовании функции на экстремум при помощи производной, не аргументированы шаги решения. Представлено доказательство вспомогательного утверждения, помогающего в решении задания. |
| 10 – 13 баллов | Найдена идея решения, но допущены ошибка на одном из начальных этапов (при использовании таблицы первообразных, ошибка при использовании формулы Ньютона-Лейбница), повлекшая за собой неправильный ответ. При допущенной ошибке дальнейшее решение выполнено верно и до конца. |
| 5 – 9 баллов | Решение не верно, но прослеживается продвижение в верном направлении. Представлено выполнение табличного интегрирования и использование свойства определенного интеграла, или использование формулы Ньютона-Лейбница и т.п. |
| 1 - 4 балла | Решение не верно, но участник приступил к решению данного задания. |
| 0 баллов | Отсутствие решения |
| 0 баллов | Участник не приступил к решению. |
|
|
|
Часть III.
№ 7. Построить график функции 
.
Решение: Найдем область определения данной функции: 
.
Область определения для функций синус и косинус – вся числовая прямая. Множество значений данных функций ограничено – это отрезок от [– 1; 1]. Проверим, выполняются ли условия области определения.
|
|
|
. (Можно и другим способом – преобразование и выделение полного квадрата).
Итак, при любых х из множества действительных чисел подкоренные выражения неотрицательны.
Подкоренные выражения данной функции представляют собой сумму разноимённых тригонометрических функций: синуса и косинуса разных аргументов, преобразуем их:
;
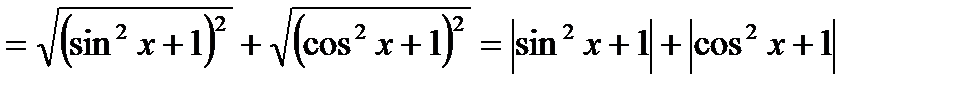Выражения, стоящие под знаком модуля представляют собой сумму двух неотрицательных слагаемых. 
.
Таким образом, после преобразований мы получили линейную функцию вида 
, графиком которой является прямая, параллельная оси ОХ и проходящая через точку с координатами (0; 3).
| у = 3 |
| 3 |
| У |
| Х |
| У |
| 0 |
| 1 |
Дата добавления: 2020-04-08; просмотров: 88; Мы поможем в написании вашей работы! |
Мы поможем в написании ваших работ!