Позиционные системы счисления

Системы счисления

Система счисления

Система счисления — это правила записи чисел с помощью специальных знаков — цифр, а также соответствующие правила выполнения операций с этими числами.

Первоначально люди считали на пальцах — это самый простой способ, который используется и сейчас. Один загнутый (или отогнутый) палец обозначал единицу (один день, одного человека, одного барана и т. п.). Такая система счисления называется унарной (от лат. unus — один). В качестве цифр унарной системы можно использовать камешки, узелки, счётные палочки (как в начальной школе), зарубки на дереве (как делал Робинзон Крузо) или на кости, чёрточки на бумаге, точки и другие одинаковые знаки или предметы.

С помощью унарной системы можно записывать только натуральные числа, причём запись больших чисел получается очень длинной (представьте себе, как записать миллион). Цифра любой позиции числа, записанного в унарной системе, всегда обозначает единицу, поэтому это одна из непозиционных систем счисления.

Непозиционная система счисления — это такая система счисления, в которой значение цифры не зависит от её места в записи числа.

К непозиционным относится и десятичная египетская система счисления. Египтяне ввели 7 знаков-иероглифов, которые обозначали степени числа 10 (чёрточка, хомут, верёвка, лотос, палец, лягушка, человек) (рис. 2.14).

Рис. 2.14

В этой системе, например, число 235 записывалось как

В римской системе счисления (она также считается непозиционной) в качестве цифр используются латинские буквы: I обозначает 1, V — 5, X — 10, L — 50, С — 100, D — 500, М — 1000. Единицы, десятки, сотни и тысячи кодировались отдельными группами, например:

2368 = 2000 + 300 + 60 + 8 = (1000 + 1000) + (100 + 100 + 100) + (50 + 10) + (5 + 1 + 1 + 1) = MMCCCLXVIII.

Больше трёх одинаковых цифр подряд не ставили, поэтому число 4 записывали как IV. В такой записи меньшая цифра (I) стоит перед большей (V), поэтому она вычитается из неё. То есть:

IV = 5 - 1 = 4.

Аналогично записывались числа 9, 40, 90, 400 и 900:

IX = 10 - 1 = 9, XL = 50 - 10 = 40, ХС = 100 - 10 = 90,

CD = 500 - 100 = 400, СМ = 1000 - 100 = 900.

Из-за этой особенности римскую систему нельзя считать полностью непозиционной, потому что значение меньшей цифры, стоящей слева от большей, меняется на отрицательное.

У римской системы есть несколько серьёзных недостатков:

• можно записывать только натуральные числа (что делать с дробными и отрицательными?);
• чтобы записывать большие числа, необходимо вводить всё новые и новые цифры (иногда использовались цифры с подчёркиванием или чертой сверху, что обозначало увеличение в 1000 раз: V — 5000, X — 10 000 и т. д.);
• сложно выполнять арифметические действия.

Сейчас римская система применяется для нумерации веков (XXI век), месяцев, глав в книгах, на циферблатах часов (например, на Спасской башне Московского Кремля).

В славянской системе счисления в качестве цифр использовались буквы алфавита, над которыми ставился знак («титло») (рис. 2.15).

Рис. 2.15

Если в ряду стояло несколько цифр, знак «титло» ставился только у первой. Старшие цифры записывались справа от младших, например, число 11 записывалось как . Славянская система счисления используется на циферблате часов Суздальского кремля.

Вопросы и задания

1. Как можно закончить фразу: «Система счисления — это...»?
2. Что такое унарная система счисления? Приведите примеры.
3. Какие недостатки имеет унарная система счисления?
4. Что такое непозиционная система счисления?
5. Какие системы счисления относятся к непозиционным?
6. Какие цифры используются в римской системе? Что они означают?
7. Можно ли называть римскую систему полностью непозиционной? Обоснуйте ответ.
8. Какое наибольшее число можно записать в классической римской системе счисления?
9. Где сейчас используется римская система?
10. Перечислите недостатки римской системы счисления. Как вы думаете, почему её не используют в компьютерах?

Подготовьте сообщение

а) «Где применяется римская система счисления?»

б) «Славянская система счисления»

в) «Системы счисления разных народов»

г) «Система остаточных классов»

Задачи

1. Переведите в римскую систему числа: 12, 345, 2999, 2444, 2888, 3777.

2. Переведите в десятичную систему числа: MCDXCIX, MMDCCXLVII, MDCXCIX.

3. Запишите в славянской системе числа: 15, 25, 38, 137, 596.

Позиционные системы счисления

Основные понятия

Позиционная система счисления — это такая система счисления, в которой значение цифры («вес») полностью определяется её местом (позицией) в записи числа.

Пример позиционной системы счисления — привычная нам десятичная система. В числе 6375 цифра 6 обозначает тысячи (т. е. 6000), цифра 3 — сотни (300), цифра 7 — десятки (70), а цифра 5 — единицы:

6375 = 6 • 1000 + 3 • 100 + 7 • 10 + 5 • 1.

Алфавит системы счисления — это используемый в ней набор цифр.

Основание системы счисления — это количество цифр в алфавите (мощность алфавита).

В десятичной системе основание — 10, алфавит состоит из 10 цифр: 0, 1, 2, 3, 4, 5, 6, 7, 8 и 9. Число 10, вероятно, было выбрано потому, что люди сначала использовали для счета свои 10 пальцев на руках.

Разряд — это позиция цифры в записи числа. Разряды в записи целых чисел нумеруются с нуля справа налево.

В числе 6375 цифра 6 стоит в третьем разряде (тысячи, 10³), 3 — во втором разряде (сотни, 10²), 7 — в первом (десятки, 10¹), а 5 — в нулевом (единицы, 10⁰). Не забывайте, что любое число (кроме нуля!) в нулевой степени равно 1. Поэтому

Это так называемая развёрнутая форма записи числа. Из этой записи видно, что последняя цифра 5 — это остаток от деления числа на 10 (все остальные слагаемые делятся на 10); число, составленное из двух последних цифр (75), — это остаток от деления исходного числа на 100 = 10² и т. д. Поэтому все числа, делящиеся на 100 без остатка, оканчиваются на два нуля.

Чтобы определить число, записанное в позиционной системе счисления, нужно значение каждой цифры умножить на основание системы счисления в степени, равной разряду этой цифры, и сложить полученные величины.

Число 6375 можно представить в другой форме — по схеме Горнера:

6375 = ((6 • 10 + 3) • 10 + 7) • 10 + 5.

Эта форма позволяет найти число, используя только умножение и деление (без возведения в степень).

Кроме десятичной системы на практике используются ещё несколько позиционных систем:

• двоичная, восьмеричная и шестнадцатеричная в компьютерной технике;
• двенадцатеричная английская система мер (1 фут =12 дюймов, 1 шиллинг = 12 пенсов);
• шестидесятеричная система измерения времени (1 час = = 60 минут, 1 минута = 60 секунд).

Целые числа

Теперь можно записать аналогичные выражения для системы счисления с любым натуральным основанием р > 1. Её алфавит состоит из р цифр ¹ от 0 до р — 1, т. е. «старшая» (наибольшая) цифра в позиционной системе счисления на единицу меньше, чем основание.

¹ При р > 10 используются также и латинские буквы, но об этом далее.

Рассмотрим четырёхзначное число а₃а₂а₁а₀, записанное в системе счисления с основанием р. Здесь а₃, а₂, а₁ и а₀ — отдельные цифры, стоящие соответственно в третьем, втором, первом и нулевом разрядах. Это число может быть записано в развёрнутой форме:

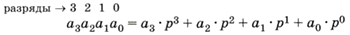
или с помощью схемы Горнера:

Оба способа можно использовать для перевода числа из любой позиционной системы в десятичную систему. Например, пусть число 12345 записано в пятеричной системе счисления (с основанием 5). Нижний индекс 5 в записи 12345 обозначает основание системы счисления (для десятичной системы основание не указывают). Тогда:

1234₅ = 1 • 5³ + 2 • 5² + 3 • 5¹ + 4 • 5⁰ = 125 + 2 • 25 + 3 • 5 + 4 = 194,

1234₅ = ((1*5 +2)* 5 + 3)* 5 + 4 = (7* 5 + 3)* 5 + 4 = 38* 5 + 4 = 194.

Схема Горнера очень удобна для обработки данных при вводе чисел с клавиатуры, когда цифры числа вводятся последовательно, начиная с первой, и их количество заранее неизвестно.

Развёрнутую запись числа можно использовать для обратного перехода, от десятичной системы к системе с основанием р. Действительно, из формулы

а₃а₂a₁а₀ = а₃ • р³ + а₂ • p² + а₁ • p + а₀ следует, что а₀ — это остаток от деления исходного числа на основание р. Если мы разделим исходное число на р и отбросим остаток, мы получим:

а₃а₂а₁ = а₃ • p² + а₂ • p + а₁.

Теперь легко найти а₁ — это последняя цифра получившегося числа, которая, как мы знаем, равна остатку от его деления на р. Разделив новое получившееся число на р и отбросив остаток, получим число

а₃а₂ = а₃ • p + а₂.

из которого найдём а₂ как остаток от деления на р. Разделив на р ещё раз, получаем последнюю цифру а₃.

Переведём, например, число 194 в пятеричную систему счисления (р = 5). Найдём остаток от деления на 5:

194 = 38*5 + 4.

Таким образом, мы нашли последнюю цифру — 4. Частное равно 38, повторяем ту же операцию:

38 = 7 • 5 + 3.

Следующая (с конца) цифра числа — 3. Дальше получаем:

7 = 1 • 5 +2,

третья с конца цифра — 2, а четвёртая — 1 (единица уже не делится на 5). Обратим внимание, что с помощью этого способа мы находим цифры числа, начиная с последней.

Поэтому полученные остатки нужно выписать в обратном порядке:

Ответ: 1234₅.

Для перевода числа из десятичной системы в систему счисления с основанием р нужно делить число на р, отбрасывая остаток на каждом шаге, пока не получится 0. Затем надо выписать найденные остатки в обратном порядке.

Можно было заметить, что такой алгоритм фактически использует схему Горнера, «раскручивая» её в обратном порядке. При каждом делении частное и остаток определяются однозначно, поэтому представление числа в любой позиционной системе единственно.

Рассмотренные приёмы позволяют записать любое неотрицательное число в заданной позиционной системе счисления. Признаком отрицательного числа служит знак «-», после которого по тем же правилам записывается модуль числа.

Пример 1. Зная десятичное число и его запись в некоторой позиционной системе счисления, можно найти основание этой системы. Пусть, например, число 71 в некоторой системе с основанием х записывается как 56_х. Представим это число в развёрнутой форме:

71 = 56_х = 5 • х¹ + 6 • х⁰ = 5 • х + 6.

Решая уравнение 71 = 5 • х + 6 относительно неизвестного х, получаем: х = 13. Значит, искомое основание системы — 13.

Пример 2. В более сложных случаях может получиться алгебраическое уравнение второй (или ещё более высокой) степени. Например, пусть то же число 71 в некоторой системе с основанием х записывается как 155_х. Представим это число в развёрнутой форме:

71 = 155_х = 1 • х² + 5 • х¹ + 5 • х⁰ = х² + 5 • х + 5.

Решая уравнение 71 = х² + 5х + 5 относительно неизвестного х, получаем два решения: х₁ = -11 и х₂ = 6. Искомое основание положительно, поэтому правильный ответ — 6.

Пример 3. Если запись числа в системе счисления задана не полностью, решений может быть несколько. Например, найдём все основания систем счисления, в которых запись десятичного числа 24 оканчивается на 3. Здесь удобно использовать схему Горнера, из которой сразу следует

24 = k • х + 3,

где х — неизвестное основание системы счисления, k — некоторое натуральное число или 0. Отсюда сразу получаем 21 — k • х, т. е. все интересующие нас основания являются делителями числа 21. Это могут быть 3, 7 и 21. Поскольку последняя цифра числа — 3, основание не может быть равно 3 (в троичной системе нет цифры 3), поэтому условию задачи удовлетворяют только основания 7 и 21.

Пример 4. Найдём все десятичные числа, не превосходящие 40, запись которых в системе счисления с основанием 4 оканчивается на 11. Используя схему Горнера, находим, что все интересующие нас числа имеют вид

N = k • 4² + 1 • 4+1 = k • 16 + 5, где k — некоторое натуральное число или 0. Подставляя k = 0, 1, 2, 3,..., находим соответствующие числа N = 5, 21, 37, 53,.... Из них только 5, 21 и 37 удовлетворяют условию (не больше 40).

Пример 5. Все 5-буквенные слова, составленные из букв А, О, У, записаны в алфавитном порядке. Вот начало списка:

1. ААААА
2. ААААО
3. ААААУ
4. АААОА

Найдём слово, которое стоит на 140-м месте от начала списка.

Как ни странно, эта задача прямо связана с позиционными системами счисления. В словах используется набор из трёх разных символов, для которых задан порядок (алфавитный). Заменив буквы А, О и У соответственно на цифры 0, 1 и 2, выпишем начало списка:

1. 00000
2. 00001
3. 00002
4. 00010

Это числа, записанные в троичной системе счисления в порядке возрастания. Тогда легко понять, что на 140-м месте от начала списка стоит десятичное число 139, записанное в троичной системе счисления:

139 = 12011₃.

Заменив обратно цифры на буквы, получаем ответ: 12011 → ОУАОО.

Вопросы и задания

1. Какие системы счисления называют позиционными?
2. Каким термином называется количество цифр в алфавите позиционной системе счисления?
3. Что такое разряд? Как нумеруются разряды?
4. Как связан в позиционной системе «вес» цифры и разряд, в котором она стоит?
5. Как вы думаете, почему в быту мы чаще всего используем десятичную систему?
6. Какие позиционные системы счисления используются сейчас на практике?
7. Чем хороша схема Горнера с точки зрения вычислений?
8. Как перевести число из любой позиционной системы в десятичную?
9. Какие цифры входят в алфавит девятеричной системы?
10. Как вы думаете, можно ли использовать систему счисления с основанием 1 000 000? В чём могут быть проблемы?
11. Сформулируйте алгоритм перевода числа из семеричной системы в десятичную.
12. Сформулируйте алгоритм перевода числа из десятичной системы в семеричную.
13. Как по записи числа в пятеричной системе сразу увидеть, делится ли оно на 5? на 25? на 125?

Задачи

1. Запишите число 12 345 в развёрнутой форме и в виде схемы Горнера.

2. Какое минимальное основание должно быть у системы счисления, чтобы в ней существовали числа 123, 463, 153 и 455? Ответ обоснуйте.

3. Выберите наибольшее число: 11₂, 11₇, 11, 11₁₂, 11₁₆, 11₂₅.

4. Переведите числа 345₆, 345₇, 345₈ и 345₉ в десятичную систему.

5. Переведите число 194 в троичную, шестеричную, семеричную и восьмеричную системы счисления.

6. Какие из чисел 1230₇, 124₇, 600₇, 530₇ делятся на 7? На 49?

7. Десятичное число, переведённое в восьмеричную и в девятеричную систему, в обоих случаях заканчивается на цифру 0. Какое минимальное десятичное число удовлетворяет этому условию?

8. Сколько всего раз встречается цифра 2 в записи чисел 10, 11, 12, ..., 17 в системе счисления с основанием 5?

9. Сколько всего раз встречается цифра 3 в записи чисел 19, 20, 21, ..., 33 в системе счисления с основанием 6?

10. В системе счисления с некоторым основанием х число 12 записывается в виде 110_х. Найдите это основание.

11. Найдите все основания систем счисления, в которых запись числа 29 оканчивается на 5.

12. В системе счисления с некоторым основанием N десятичное число 129 записывается как 1004_N. Найдите это основание.

13. Запись числа 30 в системе счисления с основанием N выглядит так: 110_N. Укажите основание N этой системы счисления.

14. Запись числа 23 в системе счисления с основанием N выглядит так: 212_N. Укажите основание N этой системы счисления.

15. Запись числа 210₅ в системе счисления с основанием N выглядит так: 313_N. Укажите основание N этой системы счисления.

16. Запись числа 65₈ в системе счисления с основанием N выглядит так: 311_N. Укажите основание N этой системы счисления.

17. Найдите все десятичные числа, не превосходящие 25, запись которых в двоичной системе счисления оканчивается на 101.

18. Запись числа 67 в системе счисления с основанием N оканчивается на 1 и содержит 4 цифры. Укажите основание N этой системы счисления.

19. Найдите все основания систем счисления, в которых запись числа 30 оканчивается на 8.

20. Найдите все основания систем счисления, в которых запись числа 31 оканчивается на 11.

21. Найдите все основания систем счисления, в которых запись числа 63 оканчивается на 23.

22. Найдите наименьшее основание системы счисления, в которой запись числа 30 трёхзначна.

23. Найдите наименьшее основание системы счисления, в которой запись числа 70 трёхзначна.

24. Найдите все десятичные числа, не превосходящие 26, запись которых в троичной системе счисления оканчивается на 22.

25. Найдите все десятичные числа, не превосходящие 30, запись которых в четверичной системе счисления оканчивается на 31.

*26. Найдите все десятичные числа, не превосходящие 25, запись которых в системе счисления с основанием 6 начинается на 4.

*27. Найдите все десятичные числа, не превосходящие 30, запись которых в системе счисления с основанием 5 начинается на 3.

*28. Найдите основание системы счисления х, для которого выполняется равенство

а) 32_х + 64_х = 106_х;
б) 45_х + 55_х = 122_х;
в) 42_х + 41_х = 133_х;
г) 91_х + 93_х = 154_х.

29. Все 5-буквенные слова, составленные из букв А, О, У, записаны в алфавитном порядке. Вот начало списка:

1. ААААА
2. ААААО
3. ААААУ
4. АААОА

Выполните следующие задания:

а) определите, сколько всего слов в списке;
б) укажите слова, которые стоят на 101-м, 125-м, 170-м и 210-м местах;
в) укажите порядковые номера слов ОАОАО, УАУАУ, АОУОА, УОАОУ;
г) укажите номера первого и последнего слов, которые начинаются с буквы О.

30. Все 5-буквенные слова, составленные из букв А, К, Р, У, записаны в алфавитном порядке. Вот начало списка:

1. ААААА
2. ААААК
3. ААААР
4. ААААУ
5. АААКА

Выполните следующие задания:

а) определите, сколько всего слов в списке;
б) укажите слова, которые стоят на 150-м, 250-м, 350-м и 450-м местах;
в) укажите порядковые номера слов АКУРА, КАРАУ, РУКАА, УКАРА, УРАКА;
г) укажите номера первого и последнего слов, которые начинаются с буквы Р.

Дробные числа

Дробные числа сначала рассмотрим на примере десятичной системы. Число 0,6375 можно представить в виде:

0,6375 = 6 • 0,1 + 3 • 0,01 + 7 • 0,001 + 5 • 0,0001.

Все множители, на которые умножаются значения цифр, представляют собой отрицательные степени числа 10 — основания системы счисления. То есть можно использовать развёрнутую форму записи, вводя отрицательные разряды:

Это число можно представить также с помощью схемы Горнера:

0,6375 = 101 • (6 + 101 • (3 + 10-1 • (7 + 101 • 5))).

Рассмотрим дробное число 0,а₁а₂а₃а₄, записанное в системе счисления с основанием р. Здесь а₄, а₂, а₃, а₄ — это отдельные цифры, стоящие соответственно в разрядах -1, -2, -3 и -4. Это число может быть записано в развёрнутой форме

или с помощью схемы Горнера:

0,а₁а₂а₃а₄ = р^-1 • (а₁ + р^-1 • (а₂ + р^-1 • (а₃ + р^-1 + a₄))).

Умножив это число на р, получаем а₁,а₂а₃а₄. Если взять целую часть результата, мы получим цифру а₁. Таким же способом можно найти оставшиеся цифры дробной части: на каждом шаге умножаем дробную часть на р и запоминаем целую часть результата — это и будет очередная цифра записи числа в системе с основанием р. Например, переведём число 0,9376 в пятеричную систему (табл. 2.2).

Чтобы получить ответ, нужно выписать все целые части результатов, полученные на каждом шаге:

0,9376 = 0,4321₅.

Вычисления заканчиваются, когда при очередном умножении дробная часть результата равна нулю. Это означает, что все остальные цифры дробной части — нули. В любом ли случае это произойдёт? К сожалению, нет. Чтобы убедиться в этом, вы можете попробовать перевести в пятеричную систему число 0,3 (должна получиться бесконечная дробь). Такая ситуация может случиться в любой системе счисления (например, вспомните, что число 1/3 записывается в виде бесконечной десятичной дроби). В этом случае обычно задают нужное количество значащих цифр и округляют число соответствующим образом.

Если нужно перевести в некоторую систему счисления число, в котором есть целая и дробная части, эти части переводят отдельно, а потом соединяют. Например, переведём число 25,375 в шестеричную систему:

25,375 = 25 + 0,375,

25 = 41₆, 0,375 = 0,213₆ ⇒ 25,375 = 41,213₆.

Вопросы и задания

1. Сформулируйте алгоритм перевода дробной части десятичного числа в шестеричную систему счисления.

2. Как вы думаете, почему не все конечные десятичные дроби можно представить в виде конечных дробей в других системах счисления?

3. Какие дробные десятичные числа можно записать в виде конечной дроби в шестеричной системе счисления? Ответ обоснуйте.

Задачи

1. Запишите число 0,12321₄ в развёрнутой форме и с помощью схемы Горнера.

2. Переведите число 15,125 в двоичную, четверичную, шестеричную и восьмеричную системы.

3. Какие из этих чисел больше, чем 1/2: 0,011₂; 0,12₃; 0,21₄; 0,22₅; 0,25₆; 0,35₇; 0,35₈?

4. Переведите числа 11,125; 15,75; 22,6875 и 30,375 в систему счисления с основанием 4.

Двоичная система счисления

Основные понятия

В двоичной системе счисления, т. е. в системе с основанием 2, алфавит состоит из двух цифр: 0 и 1. Все данные в компьютерных устройствах хранятся и обрабатываются как числа, представленные в двоичной системе счисления.

Для перевода натуральных чисел из десятичной системы в двоичную можно использовать общий алгоритм, описанный в предыдущем параграфе (деление на 2 и выписывание остатков в обратном порядке). Например, переведём в двоичную систему число 19:

Кроме того, можно использовать метод подбора, или табличный метод (разложение числа на сумму степеней двойки). Так, в числе 77 старшая степень двойки — это 64 = 2⁶ (следующая степень, 128 = 2⁷, уже больше, чем 77), поэтому

77 = 2⁶ + 13.

Теперь выделяем старшую степень двойки в числе 13: это 8 = 2³, так что

77 = 2⁶ + 2³ + 5.

Выделяем старшую степень двойки в числе 5: это 4 = 2², получаем:

77 = 2⁶ + 2³ + 2² + 1 = 2⁶ + 2³ + 2² + 2⁰.

Мы разложили число на сумму степеней двойки. Для «полного комплекта» здесь не хватает 2⁵, 2⁴ и 2¹, но можно считать, что эти степени умножаются на нули:

Это развёрнутая запись числа в двоичной системе счисления, поэтому краткая запись состоит из цифр, обведённых кружками. Единицы стоят в шестом, третьем, втором и нулевом разрядах:

Для перевода из двоичной системы в десятичную можно использовать сложение степеней двойки, соответствующих единичным разрядам:

Кроме того, иногда удобно применять схему Горнера. В первом столбце таблицы записывают цифры в разрядах двоичного числа, начиная со старшей. Вычисления начинаются с 1 (старший разряд всегда равен 1, если число — не ноль). В каждой из следующих строчек результат, полученный в предыдущей строчке, умножается на 2, и к нему прибавляется очередная цифра двоичного числа (из первой ячейки той же строки) (табл. 2.3).

Арифметические операции

Двоичные числа, как и десятичные, можно складывать в столбик, начиная с младшего разряда. При этом используют следующие правила (таблицу сложения):

0 + 0 = 0,
1 + 0 = 1,
1 + 1 = 10₂,
1 + 1 + 1 = 11₂.

В двух последних случаях, когда сумма 2 = 10₂ или 3 = 11₂ не может быть записана с помощью одного разряда, происходит перенос в следующий разряд.

Например, сложим в столбик двоичные числа 10110₂ и 111011₂. Единицы сверху обозначают перенос из предыдущего разряда:

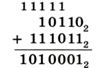
Вычитание выполняется почти так же, как и в десятичной системе. Вот правила вычитания:

0 - 0 = 0,
1 - 0 = 1,
1 - 1 = 0,
10₂ — 1 = 1.

В последнем случае приходится брать заём из предыдущего разряда. Именно этот вариант представляет наибольшие сложности, поэтому мы рассмотрим его подробно.

Чтобы понять принцип, временно вернёмся к десятичной системе. Вычтем в столбик из числа 21 число 9:

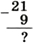
Поскольку из 1 нельзя вычесть 9, нужно взять заём из предыдущего разряда, в котором стоит 2. В результате к младшему разряду добавляется 10 (основание системы счисления), а в следующем разряде 2 уменьшается до 1. Теперь можно выполнить вычитание: 1 + 10 - 9 = 2. В старшем разряде вычитаем из оставшейся единицы ноль:

Здесь точкой сверху обозначен разряд, из которого берётся заём.

Более сложный случай — заём из дальнего (не ближайшего) разряда. Вычтем 9 из 2001. В этом случае занять из ближайшего разряда не удаётся (там 0), поэтому берем заём из того разряда, где стоит цифра 2. Все промежуточные разряды в результате заполняются цифрой 9, это старшая цифра десятичной системы счисления:

Что изменится в двоичной системе? Когда берется заём, в «рабочий» разряд добавляется уже не 10, а 10₂ = 2 (основание системы счисления), а все «промежуточные» разряды (между «рабочим» и тем, откуда берётся заём) заполняются не девятками, а единицами (старшей цифрой системы счисления). Например:

Если требуется вычесть большее число из меньшего, вычитают меньшее из большего и ставят у результата знак «минус»:

Умножение и деление столбиком в двоичной системе выполняются практически так же, как и в десятичной системе (но с использованием правил двоичного сложения и вычитания):

Таблица сложения, вычитания и умножения для двоичной системы счисления

Сложение	Вычитание	Умножение
0 + 0 = 0	0 — 0 = 0	0 ∙ 0 = 0
0 + 1= 1	1 — 0 = 1	0 ∙ 1 = 0
1 + 0 = 1	1 — 1 = 0	1 ∙ 0 = 0
1 + 1 = 10	10 — 1 = 1	1 ∙ 1 = 1

Дробные числа

Для перевода дробного числа в двоичную систему используется общий подход, описанный в § 10. В данном случае нужно умножать число на 2, запоминать целую часть и отбрасывать её перед следующим умножением. Например, для числа 0,8125 получаем табл. 2.4.

Таким образом, 0,8125 = 0,1101₂.

Давайте посмотрим, как хранится в памяти число 0,6. Выполняя умножение на 2 и выделение целой части, мы получим периодическую бесконечную дробь:

0,6 = 0,100110011001₂... = 0,(1001)₂.

Это значит, что для записи десятичного числа 0,6 в двоичной системе счисления требуется бесконечное число разрядов. Поскольку реальный компьютер не может иметь бесконечную память, число 0,6 в двоичном представлении хранится в памяти с ошибкой ¹ (погрешностью).

¹ Последний стандарт кодирования вещественных чисел IEEE 754-2008 позволяет записывать в память числа в десятичном виде. Однако вычисления с такими данными сложнее и медленнее, чем с двоичными. Кроме того, проблема конечного числа разрядов остаётся: десятичная дробь, равная 1/3, по-прежнему не может быть точно представлена в памяти компьютера.

Большинство дробных чисел хранится в памяти с некоторой погрешностью. При выполнении вычислений с дробными числами погрешности накапливаются и могут существенно влиять на результат.

Отметим, что эта проблема связана не с двоичной системой, а с ограниченным размером ячейки памяти компьютера, отведённой на хранение числа. В любой системе счисления существуют бесконечные дроби, которые не могут быть точно представлены конечным числом разрядов.

Обеспечение точности расчётов с дробными (вещественными) числами — это очень важная и актуальная проблема, пока до конца не решённая. Поэтому сначала надо попытаться решить задачу, используя только операции с целыми числами. Например, пусть требуется определить, верно ли, что , где А и В — целые неотрицательные числа. При извлечении квадратного корня мы сразу переходим в область вещественных чисел, где могут возникнуть вычислительные ошибки.

Вместо этого можно возвести обе части неравенства в квадрат и проверять равносильное условие А² < В, используя только операции с целыми числами.

Если же всё-таки нужно обязательно использовать дробные числа и нельзя жертвовать точностью, приходится хранить их в нестандартном виде, например в виде отношения целых чисел (например, 0,6 = 6/10), и вычислять отдельно числители и знаменатели простых дробей, переходя к вещественным числам только при выводе конечного результата. Этот подход применяется в системах символьных вычислений, например в программных системах Maple (www.maplesoft.com) и Mathematica (www.wolfram.com). Однако выполнение таких расчётов занимает очень много времени.

Выводы

Двоичная система счисления служит основой всех расчётов в современных компьютерах. Она обладает следующими преимуществами:

• для того чтобы построить компьютер, работающий с двоичными данными, достаточно иметь устройства с двумя состояниями (включено/выключено); первыми такими устройствами были электромагнитные реле, сейчас применяются микроэлектронные элементы;
• надёжность и защита от помех при передаче информации (для приёма двоичного кода не нужно точно измерять сигнал, достаточно знать, какое из двух значений он принимает в каждый заданный момент времени);
• компьютеру проще выполнять вычисления с двоичными числами, нежели с десятичными; например, умножение фактически сводится к многократному сложению, а деление — к вычитанию.

Тем не менее, с точки зрения человека, у двоичной системы есть недостатки:

• двоичная запись чисел получается длинная: например, число 1024 записывается в виде 10000000000₂ — здесь легко перепутать количество идущих подряд нулей;
• запись однородна, т. е. содержит только нули и единицы; поэтому при работе с двоичными числами легко ошибиться или запутаться.

Вопросы и задания

1. Как вы думаете, какие дробные числа могут быть точно представлены в памяти компьютера в двоичном коде?
2. Почему рекомендуется выполнять вычисления, используя только операции с целыми числами, если есть такая возможность?
3. Как можно работать с дробными числами, не теряя в точности? В чём недостатки такого подхода?

Подготовьте сообщение

«Двоичная система счисления с точки зрения человека и компьютера»

Задачи

1. Переведите числа 25, 31, 37, 63, 85, 127, 128 в двоичную систему счисления.

2. Переведите числа 100011₂, 101101₂, 110111₂, 1001011₂, 1011111₂, 1101001₂ в десятичную систему счисления.

3. Сколько единиц в двоичной записи чисел 173, 195, 126, 208?

4. Сколько значащих нулей в двоичной записи чисел 48, 73, 96, 254?

5. Как по записи числа в двоичной системе счисления определить, что оно чётное? Делится на 4? Делится на 8? Делится на 32?

6. Выполните сложение в двоичной системе:

а) 1010111₂ + 110101₂;
б) 1011111₂ + 111011₂;
в) 101101₂ + 11111₂;
г) 10111₂ + 101110₂;
д) 111011₂ + 11011₂;
е) 111011₂ + 10011₂.

Для проверки повторите вычисления, переходя к десятичной системе, а потом преобразуя результат обратно в двоичную.

7. Выполните вычитание в двоичной системе:

а) 101101₂ - 11111₂;
б) 11011₂ - 110101₂;
в) 10111₂ - 101110₂;
г) 101011₂ - 11011₂;
д) 1011₂ - 100101₂;
е) 1001₂ - 101101₂.

8. Переведите в двоичную систему числа 13,125; 23,25; 37,375; 48,625; 78,875.

9. Переведите в двоичную систему числа 11,8; 15,3; 22,7, выделив период в дробной части.

10. Требуется определить, верно ли, что среднее арифметическое 100 целых чисел превышает 0,2. Как сделать это, не используя операции с дробными числами?

Дата добавления: 2019-11-16; просмотров: 1208; Мы поможем в написании вашей работы!

Поделиться с друзьями:

Мы поможем в написании ваших работ!