Рассмотрим конкретный пример.

Цепь с емкостью и активным сопротивлением

Про­цес­сы в це­пи с ем­ко­стью и ак­тив­ным со­про­тив­ле­ни­ем (рис. 5.1, а) мо­гут быть про­ана­ли­зи­ро­ва­ны по ана­ло­гии с це­пью, со­дер­жа­щей ин­дук­тив­ность и актив­ное со­про­тив­ле­ние.

Рис. 5.1. Элек­три­че­ская цепь с ем­ко­стью и ак­тив­ным сопротивлением: а — схе­ма ЭЦ; б — тре­уголь­ник на­пря­же­ний; в — треугольник со­про­тив­ле­ний; г — тре­уголь­ник мощ­но­стей

От­ме­тим толь­ко, что на­пря­же­ние це­пи от­ста­ет от то­ка на угол φ (рис. 5.1, б). При этом пол­ное со­про­тив­ле­ние мож­но най­ти из тре­уголь­ни­ка со­про­тив­ле­ний (рис. 5.1, в), а пол­ную мощ­ность — из треугольни­ка мощ­но­стей (рис. 5.1, г).

 

Последовательное включение катушки индуктивности и конденсатора

Для не­раз­ветв­лен­ной ЭЦ, со­дер­жа­щей ка­туш­ку ин­дук­тив­но­сти с ак­тив­ным со­про­тив­ле­ни­ем R и ин­дук­тив­но­стью L и кон­ден­са­тор емкостью С (рис. 2.1, а), пол­ное со­про­тив­ле­ние:

Ха­рак­тер на­груз­ки за­ви­сит от ве­ли­чи­ны и зна­ка уг­ла φ, опре­де­ля­е­мо­го соотно­ше­ни­ем ин­дук­тив­но­го X_L и ем­кост­но­го X_С со­про­тив­ле­ний. В об­щем случае угол φ мо­жет из­ме­нять­ся от −π/2 до +π/2.

Рис. 2.1. Элек­три­че­ская цепь с ре­аль­ной ка­туш­кой ин­дук­тив­но­сти и конден­са­то­ром: а — схе­ма ЭЦ; б — тре­уголь­ник на­пря­же­ний; в — треугольник со­про­тив­ле­ний; г — тре­уголь­ник мощ­но­стей

 

Ес­ли X_L < X_С, то ЭЦ но­сит ем­кост­ной ха­рак­тер и угол φ < 0. Ес­ли X_L > X_С, то ЭЦ но­сит ин­дук­тив­ный ха­рак­тер и угол φ > 0.

В со­от­вет­ствии со вто­рым за­ко­ном Кирх­го­фа для мгно­вен­ных зна­че­ний напря­же­ний спра­вед­ли­во вы­ра­же­ние u = u_R + u_C + u_L, для век­то­ров — Ū = Ū_R + Ū_C + Ū_L. Век­тор­ная диа­грам­ма на­пря­же­ний по­стро­е­на от­но­си­тель­но об­ще­го для всех эле­мен­тов ЭЦ то­ка I (рис. 2.1, б). Тре­уголь­ник со­про­тив­ле­ний при­ни­ма­ет вид, при­ве­ден­ный на рис. 2.1, в, а тре­уголь­ник мощ­но­стей — на рис. 2.1, г.

Резонанс напряжений

Прак­ти­че­ский ин­те­рес пред­став­ля­ет слу­чай, ко­гда φ = 0. Это мо­жет иметь ме­сто, ес­ли Х_L = Х_C. В дан­ном слу­чае соб­ствен­ные ко­ле­ба­ния, воз­ни­ка­ю­щие в ЭЦ, сов­па­да­ют с вы­нуж­ден­ны­ми ко­ле­ба­ни­я­ми, со­зда­ва­е­мы­ми ис­точ­ни­ком пита­ния. При этом U = IR, т. е. сдвиг фаз меж­ду то­ком и на­пря­же­ни­ем отсутству­ет. Ток I = U/R мак­си­ма­лен, так как ми­ни­маль­но пол­ное сопротивление це­пи (Z = R). В свя­зи с этим на­пря­же­ния на ка­туш­ке индуктивно­сти и кон­ден­са­то­ре рав­ны (U_L = IX_L = U_C = IX_C), мак­си­маль­ны и могут зна­чи­тель­но пре­вы­шать на­пря­же­ние пи­та­ния, ес­ли Х_L = Х_C ≫ R.

В тех­ни­ке яв­ле­ние уве­ли­че­ния на­пря­же­ния на от­дель­ных эле­мен­тах ЭЦ по отно­ше­нию к на­пря­же­нию ис­точ­ни­ка пи­та­ния по­лу­чи­ло на­зва­ние ре­зо­нанс на­пря­же­ний.

Ре­зо­нанс­ная ча­сто­та в элек­три­че­ской це­пи с ка­туш­кой ин­дук­тив­но­сти и конден­са­то­ром, на­зы­ва­е­мой в ра­дио­тех­ни­ке LC-кон­ту­ром, рав­на ча­сто­те напря­же­ния, под­во­ди­мо­го к це­пи.

Из усло­вия Х_L = Х_C, или 2πfL = 1/2(πfC) мо­жет быть по­лу­че­но вы­ра­же­ние для ре­зо­нанс­ной ча­сто­ты:

Для про­мыш­лен­ной ча­сто­ты f = 50 Гц мож­но за­пи­сать при­бли­жен­ное выраже­ние, свя­зы­ва­ю­щее меж­ду со­бой зна­че­ния ре­зо­нанс­ной ем­ко­сти и индуктив­но­сти:

По­сколь­ку при ре­зо­нан­се на­пря­же­ний ток в це­пи опре­де­ля­ет­ся толь­ко лишь ак­тив­ной со­став­ля­ю­щей со­про­тив­ле­ния це­пи, об­мен ре­ак­тив­ной мощ­но­стью меж­ду це­пью и ис­точ­ни­ком от­сут­ству­ет. Ре­ак­тив­ная мощ­ность цир­ку­ли­ру­ет внут­ри кон­ту­ра от ка­туш­ки ин­дук­тив­но­сти к кон­ден­са­то­ру и об­рат­но. При этом энер­гия элек­три­че­ско­го по­ля кон­ден­са­то­ра пе­ре­хо­дит в энер­гию маг­нит­но­го по­ля ка­туш­ки ин­дук­тив­но­сти, и на­обо­рот. Ко­эф­фи­ци­ент мощ­но­сти:

cosφ = P/S = 1.

Рассмотрим конкретный пример.

Задача: Последовательно с катушкой, активное сопротивление которой R ₁=10 Ом и индуктив­ность L=0,0318 Гн, включен прием­ник, обладающий активным сопро­тивлением R₂=1 Ом и емкостью С=796 мкф (рис. I). К цепи при­ложено переменное напряжение, изменяющееся по закону u=169,8·sin(314·t).

R1

R2

L

C

U R1

UL

U R2

UC

U

I

 

 

Рис. 1. Схема электрической цепи.

Определить: полное сопротив­ление цепи, коэффициент мощно­сти цепи, ток в цепи, активную, реактивную и полную мощности, а также построить в масштабе векторную диаграмму.

Дано: ЭЦпеременного тока;

R₁=10 Ом;    L=0,0318 Гн;      R₂=1 Ом; С=796 мкФ; u=169,8·sin(314·t).

Найти: Z - ?; cos φ - ?; I - ?; P - ?; Q - ?; S - ?; построить в масштабе векторную диаграмму.

Решение:

1. Сравнивая закон изменения напряжения о цепи с общим выражением u = U_M·sin(ω t) , можно заключить, что амплиту­да напряжения U_M=169,8 B, а ω=2π · f=314 (1/сек).

Отсюда действующее значение напряжения

Частота тока

2. Индуктивное сопротивление катушки

X_L= ω L =2π · f · L =2·3.14·50·0.0318=10 Ом.

3. Емкостное сопротивление конденсатора

4. Полное сопротивление цепи

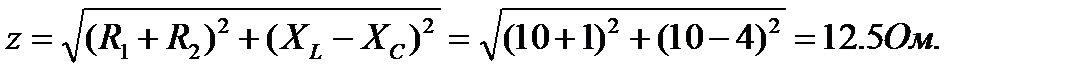
5. Коэффициент мощности цепи

φ=28,35ْ

6. Сила тока в цепи

7. Активная мощность

P = I ²(R₁+R₂)=9.6²(10+1)=1014 Bт.

или

P = U · I ·cos φ = 120·9.6·0.88=1014 Вт.

8. Реактивная мощность

Q=I²X_L- I²X_C=I²(X_L-X_C)=9.6²(10-4)=553 Вар.

или

Q=I·U·sin φ=120·9.6·0.49=553 Вар.

9. Полная мощность

S = I ² z =9.6²·12.5=1152 ВА

или

S = U · I =120·9.6=1152 BA

или

10. Построение векторной диаграммы начинаем с определения потерь напряжений на каждом сопротивлении:

U_R1=I·R₁=9.6·10=96(В);

U_R2=I·R₂=9.6·1=9,6(В);

U_L=I·X_L=9.6·10=96(В);

U_C=I · X_C=9.6·4=38,4(В);

 

 

0 20 40 60 80 100 120 140

U R1

U R2

U L

U C

U

I

φ

 

 

Рис.2. Векторная диаграмма напряжений

Затем выбираем масштаб для напряжений (см. рис. 2). Построение диаграммы начинаем с вектора тока I, который от­кладываем по горизонтали вправо от точки О (рис. 2). Вдоль векто­ра тока откладываем в принятом масштабе напряжения U_R1 и U_R2 теряемые в активных сопротивлениях цепи. Эти напряжения совпа­дают по фазе с током. От конца вектора U_R2 откладываем в сторону опережения вектора тока под углом 90° вектор потери напряжения U_L в индуктивном сопро­тивлении. Из конца векто­ра U_L откладываем вектор U_C в сторону отставания от вектора тока на угол 90^°. Геометрическая сумма че­тырех векторов равна пол­ному напряжению, прило­женному к цепи, т. е.

U = U_R1+ U_R2+ U_L+ U_C.

11. Проверку выполним, измерив транспортиром угол φ и линейкой длину вектора полного напряжения U. Получим:

U_изм = U_расч; φ_изм = φ_расч.

Из этих истинных равенств можно сделать вывод, что задача решена верно.

12. Ответ: Z = 12,5 Ом; cos φ = 0,88; I = 9,6 А; P = 1014 Bт; Q = 553 Вар;

S = 1152 BA.

---

Дата добавления: 2020-01-07; просмотров: 655; Мы поможем в написании вашей работы!

Поделиться с друзьями:

---

---

Мы поможем в написании ваших работ!