Минимизация пути на графе. Жадный алгоритм. Алгоритм Дейкстры
Изоморфизм графов
2.1. Попробовать для двух неориентированных графов, представленных геометрически, показать их изоморфизм, задав соответствующую нумерацию вершин.
Решение.
Проверим сначала, что число рёбер совпадает. Причём совпадение должно быть не только по сумме, но и по количеству рёбер у каждой пары вершин сравниваемых графов. То, что число рёбер совпадает, – очевидно. Число рёбер 1-го графа = 14. Число рёбер 2-го графа = 14. Методом подбора находим новую нумерацию вершин 2-го графа, соответствующую вершинам 1-го графа. В качестве p1 можем взять любую из точек qi. Пусть p1 = q1. В качестве p2 пробуем взять q2. Так как в первом графе p1 и p2 соединены с p7, а на втором с q5, то q5 = p7. Рассуждая подобным образом, приходим к противоречию. Поэтому в качестве p2 нельзя брать q2. В конце концов находим, что в качестве p2 можно взять q4.
В этом случае соответствие остальных вершин pi и qj находится, что показано на рисунке. Кстати, возможен и другой вариант, когда в качестве p2 берётся q5. Учитывая, что в качестве p1 можно было взять 7 вариантов точек, получаем 2x7=14 вариантов перенумерации вершин 2-го графа, показывающих изоморфизм двух графов. 5.
2.2. Показать, что два неориентированных графа неизоморфны
Решение1.
Проверим сначала, что степени вершин совпадают. Да, это так. Если бы степени вершин у двух графов отличались, то это сразу показало бы отсутствие изоморфизма. Можно заметить, что на первом графе имеется последовательность из восьми смежных рёбер, возвращающаяся к начальной вершине. В этом цикле все вершины проходятся по одному разу.
|
|
|
Например, его можно задать перечислением вершин p1, p2, p3, p4, p8, p7, p6, p5, p1. При этом некоторые рёбра остались неиспользованными.
Можно эту же
последовательность рёбер начинать с любой другой вершины, в которой последовательность рёбер и закончится. Это означает, что каждая вершина в данном цикле имеет только два смежных ребра.
Чтобы графы были изоморфны, необходимо, но не достаточно, чтобы аналогичная последовательность имелась во втором графе. Предположим, что это так.
Во втором графе вершины q2 и q4 имеют каждая только по два смежных ребра, следовательно, эти четыре ребра должны быть в последовательности рёбер соответствующего цикла, но тогда для перехода к вершинам q5, q6, q7, q8 необходимо использовать ребро (q1, q5) или (q3, q7).
Следовательно, в соответствующей последовательности вершин и рёбер второго графа будет вершина, из которой исходят три ребра, чего быть не может. В цикле из каждой вершины может исходить только 2 ребра. Следовательно, наше предположение не верно, т.е. два графа не изоморфны.
|
|
|
Решение 2.
Это решение аналогично предыдущему, но сделано с использованием понятия “гамильтонов цикл”. Это цикл, проходящий через все вершины по одному разу. У первого графа имеется гамильтонов цикл p1, p2, p3, p4, p8, p7, p6, p5, p1. Чтобы был изоморфизм, второй граф тоже должен иметь гамильтонов цикл. Так как вершины q2, q4, q6, q8 – двухвалентны, то все рёбра, исходящие из них, должны присутствовать в этом гамильтоновом цикле. Для вершин q2, q4 это четыре ребра q1-q2-q3-q4q1. Для вершин q6, q8 это четыре ребра q5-q6-q7-q8-q5. Так как в гамильтоновом цикле в каждой вершине должны быть использованы только 2 ребра, следовательно, рёбра q1-q5 и q3-q7 не могут быть использованы. Но тогда от вершин q1, q2, q3, q4 невозможно перейти к вершинам q5, q6, q7, q8. Следовательно, предположение, что 2-й граф имеет гамильтонов цикл, неверно. Графы не изоморфны, так как обладают разными свойствами.
2.3. Для двух неориентированных графов, представленных геометрически, показать их изоморфизм, задав соответствующую нумерацию вершин.
Решение.
Проверим сначала, что число рёбер совпадает. Причём совпадение должно быть не только по сумме, но и по количеству рёбер у каждой пары вершин сравниваемых графов. То, что число рёбер совпадает, – очевидно. Число рёбер 1-го графа = 
|
|
|
Число рёбер 2-го графа = 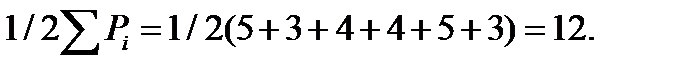
Методом подбора находим новую нумерацию вершин 2-го графа, соответствующую вершинам 1-го графа.
2.4. Показать, что два неориентированных графа неизоморфны, путём поиска соответствующей перенумерации вершин или другим способом.
Решение 1.
Последовательности вершин p1, p5, p8, p4, p1, образующей цикл, в случае изоморфизма графов должна соответствовать последовательность, включающая вершины q1, q5, q3, q7, так как только эти вершины имеют степени, совпадающие со степенями вершин p1, p5, p8, p4. Но эти четыре вершины q1, q5, q3, q7, очевидно, не могут быть соединены четырьмя рёбрами в цикл, как вершины p1, p5, p8, p4. Следовательно, графы не изоморфны.
Решение 2.
Вершина p1, степени 3, связана рёбрами с двумя вершинами p4 и p5, со степенями также 3. Аналогичной p1 вершины среди вершин qi нет. Например, вершина q1, степени 3, связана ребром только с одной вершиной степени 3. Таким образом, оба графа имеют различные свойства и, следовательно, графы не изоморфны.
2.5. Для двух неориентированных графов, представленных геометрически, показать их изоморфизм, задав соответствующую нумерацию вершин:
|
|
|
Решение.
2.6. Показать, что два неориентированных графа неизоморфны, путём поиска соответствующей перенумерации вершин или другим способом:
3. Элементы графов и орграфов. Эйлеров цикл. Плоские и планарные графы
3.1. Для неориентированного графа:
1) построить матрицу инцидентности; 2) указать степени вершин графа;
3) найти длину маршрута из вершины p2 в вершину p5 , составить маршруты длины 5, указать все цепи и элементарные цепи, соединяющие вершину p2 и вершину p5 ;
4) построить простой цикл, содержащий вершину p4 ;
5) найти цикломатическое число графа, равное увеличенной на 1 разности между числом рёбер и числом вершин графа;
6) определить вид заданного графа;
7) является ли граф эйлеровым, т.е. содержит ли цикл, содержащий все рёбра графа, причём каждое ребро в точности по одному разу?
8) существует ли эйлеров путь в графе, т.е. такой путь, когда все рёбра проходятся по одному разу, но без возвращения в исходную точку?
3.2. Для ориентированного графа:
1) построить матрицу инцидентности;
2) имеются ли здесь источники и стоки?
3.3. Для неориентированного графа, заданного матрицей инцидентности:
| u1 | u2 | u3 | u4 | u5 | u6 | Дуги/вершины |
| 0 | 0 | 1 | 1 | 0 | 1 | p1 |
| 1 | 0 | 1 | 1 | 0 | 1 | p2 |
| 0 | 0 | 0 | 0 | 1 | 0 | p3 |
| 1 | 1 | 0 | 0 | 1 | 0 | p4 |
| 0 | 0 | 0 | 0 | 0 | 0 | p5 |
1) восстановить геометрическое представление;
2) построить простой цикл, содержащий вершину p4 ;
3) найти цикломатическое число графа, равное увеличенной на 1 разности
между числом рёбер и числом вершин графа;
4) определить вид заданного графа. (Ориентированный или нет, циклический или нет, простой или нет). Простой граф – граф, в котором нет кратных ребер и петлей.
3.4. Задан неориентированный граф:
Что из приведённого ниже является путём в графе и которые из них являются простыми путями? Приведите длину каждого из путей:
1) p4p1p2p3p6p2;
2) p1p2p3p2p4p2;
3) p1p2p3p4p5p6p1;
4) p2p4p3p2.
3.5. Для неориентированного графа:
1) определить степени вершин и по ним число рёбер графа;
2) что из приведённого ниже является путём в графе и которые из них являются
простыми путями? (Простой путь, он же путь Гамильтона, не содержит
повторяющихся вершин)
3) определить длину каждого из путей.
а) p1p5p2p4p3p6; +
б) p1p5p2p5p3p4p2p6;
в) p1p6p5p1p6p5p3;
г) p6p5p3p4p5p1.
3.6. Задан неориентированный графа:
Что из приведённого ниже является циклом в графе?
Которые из них являются простыми циклами?
1) p4p1p2p3p6p2p5p4;
2) p4p5p6p1p2p3p4; - цикл, но не простой.
3) p1p2p3p6p5p2p6p3p1;
4) p2p6p3p5p4p2p6.
3.7. Является ли следующий граф планарным? ( нет)
3.8. Для неориентированного графа:
1) построить матрицу инцидентности;
2) указать степени вершин графа;
3) построить простой цикл, содержащий вершину p4 ;
4) найти цикломатическое число графа, равное увеличенной на 1 разности между числом рёбер и числом вершин графа;
6) определить вид заданного графа;
7) является ли граф эйлеровым, т.е. содержит ли цикл, содержащий все рёбра графа, причём каждое ребро в точности по одному разу?
8) существует ли эйлеров путь в графе, т.е. такой путь, когда все рёбра проходятся по одному разу, но без возвращения в исходную точку?
3.9. Для ориентированного графа:
1) обозначить дуги;
2) построить матрицу инцидентности;
3) имеются ли здесь источники и стоки?
3.10. Для ориентированного графа, заданного матрицей инцидентности:
| u1 | u2 | u3 | u4 | u5 | u6 | Дуги/вершины |
| 0 | 1 | 0 | -1 | 0 | -1 | p1 |
| -1 | 0 | -1 | 1 | 0 | 1 | p2 |
| 0 | 0 | 1 | 0 | 1 | 0 | p3 |
| 1 | 0 | 0 | 0 | 0 | 0 | p4 |
| 0 | 0 | 0 | 0 | 0 | 0 | p5 |
1) восстановить геометрическое представление;
2) определить степень входа и степень выхода каждой вершины графа.
Имеются ли здесь источники и стоки?
3.11. Для неориентированного графа:
Что из приведённого ниже является путём в графе?
Которые из них являются простыми путями?
Приведите длину каждого из путей:
1) p4p1p2p3p6p2;
2) p1p2p3p2p4p2;
3) p1p2p3p4p5p6p1;
4) p2p4p3p2.
3.12. Для неориентированного графа:
1) определить степени вершин и по ним число рёбер графа;
2) что из приведённого ниже является путём в графе? Которые из них являются простыми путями?
Приведите длину каждого из путей:
а) p1p5p2p4p3p6;
б) p1p5p2p5p3p4p2p6;
в) p1p6p5p1p6p5p3;
г) p6p5p3p4p5p1.
3.13. Для неориентированного графа:
Что из приведённого ниже является циклом в графе? Которые из них являются простыми циклами?
1) p4p1p2p3p6p2p5p4; 2) p4p5p6p1p2p3p4;
3) p1p2p3p6p5p2p6p3p1; 4) p2p6p3p5p4p2p6.
3.14. Является ли следующий граф планарным?
3.15. Является ли следующий граф планарным?
Графы. Деревья.
4.1. На приведенном рисунке изображена схема зоопарка (вершины графа – вход, выход, перекрёстки, повороты, тупики, рёбра-дорожки, вдоль которых расположены клетки). Найдите маршрут, по которому экскурсовод мог бы провести посетителей, показав им всех зверей и не проходя более одного раза ни одного участка пути, т.е. найдите эйлеров путь.
Решение. Найденный маршрут, т.е. эйлеров путь, показан на рисунке номерами у вершин и стрелками у рёбер.
4.2. По правилу Тарри найдите замкнутый путь из вершины А, содержащий все рёбра графа дважды, по одному разу в каждом направлении.
Правило Тарри
Из произвольной вершины А пройдём вдоль какого-нибудь ребра (А,В), отметив его стрелкой, указывающей направление пути. Из В пройдём к третьей вершине, снова отметив стрелкой направление прибытия, и так далее. Ребро, по которому впервые прибываем в вершину, будем отмечать стрелкой вида " •à ".
Выходя из вершины, выбирают дальнейший путь: либо ребро, по которому ещё не проходили ни разу, либо ребро, по которому прибыли в эту вершину. Договариваемся, что ребро, по которому впервые попали в вершину, будем использовать для выхода только тогда, когда оно остаётся единственным выходом из этой вершины.
Продолжаем строить путь, пока это возможно. Итак, задан граф:
Решение. Решение, полученное согласно правилу Тарри, показано на рисунке занумерованными числами около рёбер графа имеет вид:
Алгоритма Флёри
Пусть Г – эйлеров граф; тогда следующая процедура всегда возможна и приводит к эйлеровому циклу графа Г. Выходим из произвольной вершины и идём по рёбрам графа произвольным образом, соблюдая лишь следующие правила:
· стираем рёбра по мере их прохождения и стираем также изолированные вершины, которые при этом образуются;
· на каждом этапе идём по мосту только тогда, когда нет других возможностей. (Мост – это ребро, которое после удаления делает граф не связным.
Хотя эйлеров граф не содержит мостов, но после удаления рёбер, могут образоваться мосты.
4.3. С помощью алгоритма Флёри найдите эйлеров цикл в графе, изображённом на следующем рисунке:
Решение.
Найденный маршрут, т.е. эйлеров путь, показан на рисунке номерами у рёбер:
4.4. Найдите эйлеровы циклы или пути на следующих графах Г1, Г2.
Граф Г1 Граф Г2
4.5. Задача о ходе коня. Можно ли ходом коня обойти шахматную доску, побывав на каждой клетке по одному разу?
4.6. Задача о ходе коня. Можно ли ходом коня обойти шахматную доску, побывав на каждой клетке по одному разу и вернуться в исходную точку?
Минимизация пути на графе. Жадный алгоритм. Алгоритм Дейкстры
5.1. Используя жадный алгоритм построить коммуникационную сеть, т.е. построить «экономичное дерево», минимизирующее сумму расстояний между вершинами связного графа, для двух вариантов (а) и (б):
(а) q12=4, q13=7, q14=11, q15=4, (б) q12=6, q13=8, q14=11,q15=4,
q23=6, q24=7, q25=11, q23=6, q24=3, q25=11,
q34=15, q45=2. q34=15, q45=9.
5.2. Для графа с весами:
qBD=7, qBC=3, qBE =11, qBA =4,
qAC=3, qAD –не задан, qAE=4,
qCE=2, qCD=15,
qDE=2,
найти кратчайшие расстояния между всеми вершинами с помощью алгоритма Декстра. С помощью полученных кратчайших расстояний между всеми вершинами исходного графа сформировать полный граф.
Решение.
Первоначально граф был задан в виде:
Имеем кратчайшие пути между всеми вершинами:
W(AB) = 4; W(AC) = 3; W(AD) = W(AED) = 6; W(AE) = 4;
W(BC) = 3; W(BD) = 7; W(BE) = W(BCE) = 5;
W(CD) = W(CED) = 4; W(CE) = 2; W(DE) = 2. Что отражено на рисунке:
Имеем полный граф, где все вершины связаны друг с другом.
5.3. Для графа с весами:
qAB=10, qAC=18, qAD – не задан, qAE=14,
qBC=12, qBD=20, qBE – не задан,
qCD=6, qCE=14, qDE=10
найти кратчайшие расстояния между всеми вершинами с помощью алгоритма Декстра. С помощью полученных кратчайших расстояний между всеми вершинами исходного графа сформировать полный граф.
Решение.
Имеем кратчайшие пути между всеми вершинами:
W(BC) = 12; W(BD) = 20; W(BА) = 10;
W(AC) = 18; W(AD) = W(AE) = 14;
W(CE) = 14; W(CD) = 6; W(DE) = 10.
Что отражено на рисунке:
Рис. 5.3.1. Начальный граф Рис. 5.3.2. Полный граф
Дата добавления: 2020-01-07; просмотров: 1219; Мы поможем в написании вашей работы! |

Мы поможем в написании ваших работ!
