Увеличении инвестиций на 5 млрд руб.
| Эндогенные переменные | Запаздывание | ||||
| 0 | 1 | 2 | 3 | 4 | |
| С t | 12,17 | –7,23 | -6,07 | 1,06 | 2,40 |
| It | 5,0 | –3,27 | -2,32 | 0,56 | 1,00 |
| IMt | 2,17 | 0,40 | -0,67 | –0,31 | 0,16 |
| Yt | 16,67 | -10,90 | –7,72 | 1,95 | 1,53 |
Каждое уравнение эконометрической модели в прогнозной форме может быть самостоятельно использовано для получения прогноза ожидаемого значения совместно зависимых переменных для одного периода. Для приема вычислим прогнозное значение личного потребления для t=10 (тогда t –1=9), используя данные таблицы, и сравним его с действительным значением.
Воспользуемся функцией потребления, объясняемой первым уравнением модели:

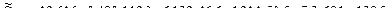 .
.
Абсолютная погрешность оценки потребления:
 ;
;
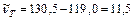 .
.
Относительная погрешность потребления за год T:
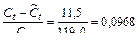 или 9,68%.
или 9,68%.
Прогноз по стационарным моделям временных рядов
Наиболее популярным методом прогнозирования является использование моделей авторегрессии и скользящего среднего (АРСС), в которых не участвуют экзогенные (независимые) переменные. Модели данного класса служат для обработки стационарных временных рядов (рядов динамики).
Модель АРСС включает две составные части:
а) авторегрессионный процесс (АР). Выражает переменную 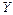 в виде функции предшествующих значений
в виде функции предшествующих значений 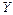 , то есть
, то есть
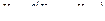 . (9.9)
. (9.9)
Модель, описываемая соотношением (9.9), называется процессом авторегрессии порядка p.
б) процесса скользящего среднего:
|
|
|
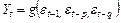 . (9.10)
. (9.10)
Модель (9.10) носит название процесс скользящего среднего порядка q.
Для построения модели АРСС следует объединить линейные формы процессов авторегрессии и скользящего среднего с моделью сдвига 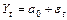 .
.
Тогда получим:
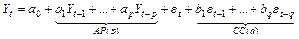 (9.11)
(9.11)
Следует заметить, что уравнение (9.11) может адекватно описывать поведение временных рядов в экономике, если ряды динамики являются стационарными. Стационарность временного ряда означает, что зависимая переменная имеет постоянную среднюю и дисперсию в течение периода наблюдения, то есть
 ,
,
а также ковариации наблюдений зависят от длины между отсчетами.
Приведем графическое изображение стационарного и нестационарного временных рядов (рис. 24).

Рис. 24
Сведение нестационарного ряда к стационарному с последующей его обработкой может быть осуществлено на основе метода последовательных разностей:
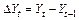 ,
, 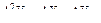 и т.д.
и т.д.
Необходимый наивысший порядок последовательных разностей, при котором нестационарный временной ряд сводится к стационарному в условии ненулевого тренда, обозначим символом d . Тогда после нахождения прогноза 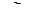 необходимо рассчитать прогноз эндогенной переменной по формуле
необходимо рассчитать прогноз эндогенной переменной по формуле 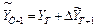 и т. д.
и т. д.
|
|
|
Модель, учитывающая последовательные разности, носит название авторегрессии и интегрированного скользящего среднего АРИСС (p , d , q). Например, АРИСС (2, 1, 1) указывает на включение в уравнение двух авторегрессионных слагаемых (из конечных разностей первого порядка) и одного слагаемого модели скользящего среднего:
АРИСС (2, 1, 1):  .
.
В условиях применения АРИСС-модели возникают три основные задачи:
· оценка структуры модели, то есть спецификация параметров p ,
d и q;
· оценка коэффициентов модели 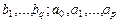 ;
;
· прогнозирование переменной 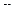 модели.
модели.
Перейдем к решению этих задач:
1. Процедура спецификации модели обычно начинается с решения задачи оценивания порядка включаемых в модель конечных разностей d.
Шаг 1. Производят изучение выборки данных, если Y проявляет тенденцию к росту, то вычисляют конечные разности 1-го поряд-
ка 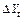 .
.
Шаг 2. Проверяют парный коэффициент корреляции 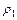 между зависимой переменной
между зависимой переменной 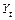 и лаговой переменной
и лаговой переменной 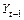 . При корректном выборе параметра d индикатор
. При корректном выборе параметра d индикатор 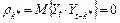 , тогда в качестве оценки
, тогда в качестве оценки 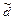 принимают k*. Изобразим алгоритм остановки процесса преобразования исходной модели к стационарной с помощью графика
принимают k*. Изобразим алгоритм остановки процесса преобразования исходной модели к стационарной с помощью графика 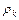 , который носит название кореллограммы:
, который носит название кореллограммы:
|
|
|
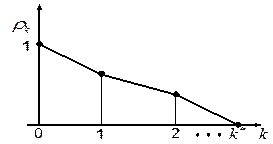
Рис.25
2. Нахождение оценок параметров авторегрессии 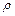 и скользящего среднего осуществляют в три этапа.
и скользящего среднего осуществляют в три этапа.
Этап 1. Выбирают начальные значения 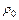 и
и 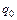 , по возможности наименьшие
, по возможности наименьшие 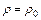 ,
, 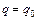 .
.
Этап 2. Оценивают АРИСС ( 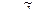 ) и находят остатки
) и находят остатки 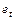 , с помощью которых рассчитывают частные коэффициенты автокорреляции:
, с помощью которых рассчитывают частные коэффициенты автокорреляции:
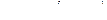 .
.
Если  , то сохраняют
, то сохраняют 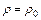 и
и 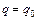 , в противном случае увеличивают начальные значения ρ и q на единицу и повторяют этап 2 для модели АРИСС (
, в противном случае увеличивают начальные значения ρ и q на единицу и повторяют этап 2 для модели АРИСС ( 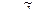 ) до тех пор, пока коэффициенты частной корреляции не обратятся в нуль.
) до тех пор, пока коэффициенты частной корреляции не обратятся в нуль.
Приведем таблицу выбора моделей низких порядков АРИСС на базе определенных значений коэффициентов корреляции.
| Модель | 
| 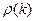
|
| Нестационарная | Отличен от нуля | Отличен от нуля |
| АРИСС(0, 0, 0) | Все равны нулю | Все равны нулю |
| АРИСС(1, 0, 0) | Стремятся к нулю | Обращаются в нуль после 1-ого лага |
| АРИСС(2, 0, 0) | Стремятся к нулю | Обращаются в нуль после 2-ого лага |
| АРИСС(0, 0, 1) | Обращаются в нуль после 1-ого лага | Стремятся к нулю |
| АРИСС(0, 0, 2) | Обращаются в нуль после 2-ого лага | Стремятся к нулю |
| АРИСС(1, 0, 1) | Обращаются в нуль после 1-ого лага | Обращаются в нуль после 1-ого лага |
Этап 3. Закончив процесс оценивания структуры модели АРИСС, переходят к оцениванию ее коэффициентов. Следует заметить, что лишь при 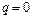 целесообразно применять классический МНК, а в противном случае требуется использовать операторы декорреляции или взвешенные модификации МНК.
целесообразно применять классический МНК, а в противном случае требуется использовать операторы декорреляции или взвешенные модификации МНК.
|
|
|
Для решения задачи нахождения прогноза используют модель
с наблюдаемыми остатками 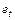 :
:
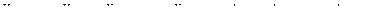
где 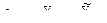 ,
, 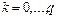 .
.
Процесс построения прогнозируемых значений происходит последовательно, начиная с оценки прогноза на один период, используя который, получают прогноз на 2 периода в будущее и так далее. Проиллюстрируем этот процесс для модели АРИСС (2, 0, 1):
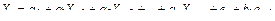 ,
, 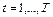 .
.
Для нахождения прогноза в момент времени Т+1 оценивают коэффициенты и после подстановки получают:
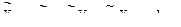 ,
,
где остаток, полученный в момент Т+1, равен нулю. Далее, для получения прогноза в момент Т+2, имеют
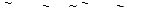 .
.
Заметим, что процесс скользящего среднего с момента Т+2 уже не участвует в прогнозировании.
Рассмотрим применение АРИСС-модели для прогнозирования темпа инфляции [17]:
Пример. В макроэкономике одной из центральных проблем является установление количественной взаимосвязи между темпом инфляции и уровнем безработицы. Современное состояние, основанное на концепции инфляционных ожиданий и расширившее классическую зависимость А.Филлипса, имеет вид [27]:
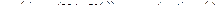 ,
,
где 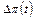 – темп инфляции в момент t;
– темп инфляции в момент t;
 – уровень безработицы в момент t;
– уровень безработицы в момент t;
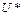 – естественный уровень безработицы, не воздействующий на темп инфляции.
– естественный уровень безработицы, не воздействующий на темп инфляции.
На основе статистических данных экономики США за 1977 – 1990 гг. об уровнях инфляции INF(t) и безработицы U(t) была построена эконометрическая модель вида:
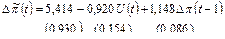 (9.12)
(9.12)
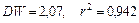 .
.
Качество модели (9.12) – достаточно высокое, действительно:
а) t-статистики оценок параметров превышают табличные пороговые значения и позволяют сделать вывод о значимости коэффициентов модели;
б) статистика Дарбина-Вотсона близка к значению 2, что говорит об отсутствии автокорреляции остатков при любом разумно малом уровне значимости α;
в) коэффициент адекватности позволяет судить об очень высокой доле дисперсии зависимой переменной, объясненной с помощью уравнения авторегрессии АРИСС (1, 1, 0).
Полученное уравнение имеет содержательную интерпретацию, которая позволяет сделать вывод о большой инерционности инфляционного процесса; более того, значение мультипликатора ( 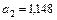 ),
),
превышающее единицу, указывает на самоускоряющийся характер этого процесса. Из уравнения (9.12) можно найти оценку естественного уровня безработицы:
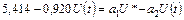 .
.
Следовательно, 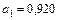 , откуда
, откуда 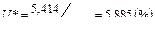 .
.
Поэтому естественный уровень безработицы в США по данным за 1977 – 1990 гг. составил около 6%.
Пример. Согласно модели экономического роста Р.Солоу страны, имеющие большую норму сбережения и обладая высокой фондовооруженностью, будут иметь и больший доход на душу населения.
Используя зависимость, соответствующую модели Солоу, эконометрическая зависимость удельного дохода примет вид:
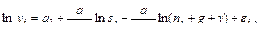 (9.13)
(9.13)
где 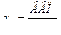 – удельный выпуск на душу трудоспособного населения L i-й страны,
– удельный выпуск на душу трудоспособного населения L i-й страны,
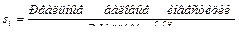 ;
;
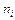 – средний темп роста численности населения i-й страны.
– средний темп роста численности населения i-й страны.
По данным экономики США за 1960 – 1985 гг. была получена оценка зависимости (9.13) [14].
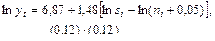
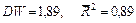
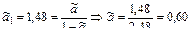 .
.
Следовательно, доля общего дохода, обусловленная основными фондами, составила 60%. Эластичность удельного ВВП по норме сбережений составила 1,48, а по темпу роста населения – (–1,48).
Среди многочисленных методов прогнозирования важную роль играют процедуры автопрогноза, в рамках которой имеющийся в наличии временной ряд подвергается экстраполяции только на базе его значений, полученных в прошлые периоды времени.
Наиболее эффективное решение задач краткосрочного и среднесрочного автопрогноза производится на основании моделей авторегрессии и интегрированного скользящего среднего АРИСС (p, d, q):
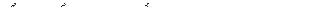 (9.14)
(9.14)
где 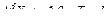 – ряд, полученный после применения к исходному ряду
– ряд, полученный после применения к исходному ряду  – кратной процедуры последовательных разностей, т.е.:
– кратной процедуры последовательных разностей, т.е.:

Частными случаями модели (9.14) являются:
модель авторегрессии AP (p)
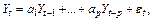 (9.15)
(9.15)
модель скользящего среднего СС (q)
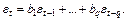 (9.16)
(9.16)
Модель (9.14) предназначена для описания нестационарных временных рядов 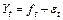 , содержащих трендовую аддитивную составляющую
, содержащих трендовую аддитивную составляющую 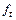 , имеющих вид алгебраического полинома степени k – 1
, имеющих вид алгебраического полинома степени k – 1 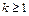 с коэффициентами любого типа (случайного или детерминированного).
с коэффициентами любого типа (случайного или детерминированного).
Модели (9.15) и (9.16) описывают стационарные (в широком смысле) временные ряды, т.е. их средние 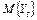 , дисперсии
, дисперсии 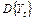 и ковариации
и ковариации 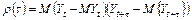 остаются постоянными в течение времени t.
остаются постоянными в течение времени t.
В теории рядов динамики основные кривые роста, описывающие трендовую составляющую 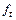 , имеют вид, представленный в табл. 9.4.
, имеют вид, представленный в табл. 9.4.
Из двух последних столбцов таблицы вытекает, что подбор кривых роста осуществляется путем вычисления характеристик прироста уровней ряда, которое выполняется по следующему алгоритму:
1. Производится сглаживание ряда динамики методом скользящей средней (т.е., для каждых 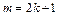 – нечетных последовательно расположенных уровней ряда вычисляют среднюю величину, далее переходят к расчету средних для уровней
– нечетных последовательно расположенных уровней ряда вычисляют среднюю величину, далее переходят к расчету средних для уровней 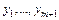 (отбрасывая первый и добавляя следующий за
(отбрасывая первый и добавляя следующий за 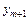 ) и т.д. Общая формула
) и т.д. Общая формула 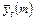 имеет вид:
имеет вид:
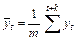 . (9.17)
. (9.17)
Таблица 9.4
| № п/п | Название кривой роста | Вид тренда | Характеристика подбора | Характер изменения во времени |
| 1 | Линейная
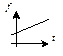
|
| 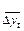
| Примерно одинаковые |
| 2 | Парабола второго порядка
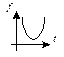
|

| 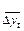
| Линейно изменяются |
| 3 | Кубическая парабола
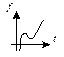
| 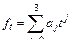
| 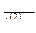
| Линейно изменяются |
| 4 | Показательная
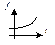
|
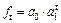
| 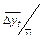
| Примерно одинаковые |
| 5 | Модифицированная показательная
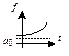
|

| 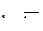
| Линейно изменяются |
| 6 | Логарифмическая парабола
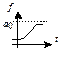
|

| 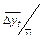
| Линейно изменяются |
| 7 | Кривая Гомперца
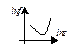
|

| 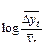
| Линейно изменяются |
| 8 | Логистическая кривая
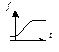
|
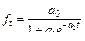
| 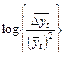
| Линейно изменяются |
Формула (9.17) допускает последовательный расчет
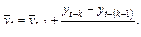 (9.18)
(9.18)
2. Вычисляют средние приросты по предварительно полученному ряду последовательных разностей соответствующих порядков (абсолютных приростов уровней ряда):
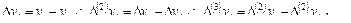
Если начало отсчета времени находится внутри интервала сглаживания длиной m, то общая формула исчисления средних приростов имеет вид:
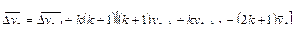 . (9.19)
. (9.19)
Наиболее используемые частные случаи:
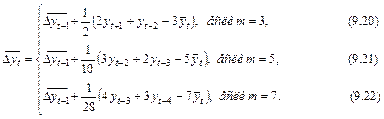 Прямое вычисление средних приростов состоит в расчете средних арифметических абсолютных приростов:
Прямое вычисление средних приростов состоит в расчете средних арифметических абсолютных приростов:
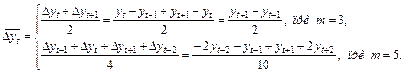
Общая формула прямого расчета (m = 2k+1):
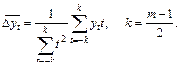 (9.23)
(9.23)
3. Образуют ряд производных характеристик от средних приростов, основные типы которых даны в третьем столбце табл. 9.1.
4. Полученный на предыдущем шаге ряд анализируется по признаку линейного развития во времени, на основании которого подбирают вид кривой роста (тренда) в соответствии с тенденцией, отмеченной в столбце 4 табл. 9.1.
Рассмотрим иллюстративный пример выбор вида кривой роста.
Пример 9.1 ¢ * Производство радиоаппаратуры на предприятии в течение 15 лет представлено в таблице:
| t | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 |
| yt | 3,6 | 4,9 | 10,3 | 12,8 | 13,7 | 14,5 | 17,1 | 24,4 | 22,9 |
| t | 10 | 11 | 12 | 13 | 14 |
| yt | 25,3 | 28,2 | 30,2 | 34,1 | 32,5 |
Расчеты характеристик приростов представленного ряда помещены в табл.9.5.
Таблица 9.5
| t | yt |
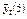
| 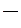
| 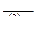
| 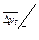
| 
| 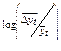
| 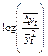
|
| 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 |
| 1 | 3,6 | --- | --- | --- | --- | --- | --- | --- |
| 2 | 4,9 | --- | --- | --- | --- | --- | --- | --- |
| 3 | 10,3 | 9,60 | 2,86 | 0 | 0,31 | 0,45 | -0,51 | -1,46 |
| 4 | 12,8 | 11,24 | 2,26 | -0,55 | 0,20 | 0,35 | -0,70 | -1,75 |
| 5 | 13,7 | 13,68 | 1,53 | -0,73 | 0,11 | 0,18 | -0,95 | -2,09 |
| 6 | 14,5 | 16,50 | 2,66 | 1,13 | 0,16 | 0,42 | -0,79 | -2,01 |
| 7 | 17,1 | 18,52 | 2,83 | 0,17 | 0,15 | 0,45 | -0,82 | -2,08 |
| 8 | 24,4 | 20,84 | 2,74 | -0,09 | 0,13 | 0,44 | -0,88 | -2,20 |
| 9 | 22,9 | 23,58 | 2,31 | -0,43 | 0,10 | 0,36 | -1,01 | -2,38 |
| 10 | 25,3 | 26,20 | 1,69 | -0,62 | 0,06 | 0,23 | -1,19 | -2,61 |
Продолжение табл. 9.5
| t | yt |
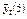
| 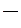
| 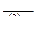
| 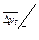
| 
| 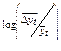
| 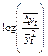
|
| 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 |
| 11 | 28,2 | 28,14 | 2,73 | 1,04 | 1,10 | 0,44 | -1,01 | -2,46 |
| 12 | 30,2 | 30,06 | 2,03 | -0,70 | 0,07 | 0,31 | -1,17 | -2,65 |
| 13 | 34,1 | --- | --- | --- | --- | --- | --- | --- |
| 14 | 32,5 | --- | --- | --- | --- | --- | --- | --- |
При рассмотрении графического изображения ряда по показателям можно сделать вывод о линейном тренде. По графикам (рис. 23) можно визуально отметить, что наибольшее приближение к линейному
развитию во времени характерно для 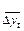 ,
, 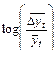 ,
, 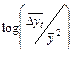 . Среди этих трех показателей, по-видимому, наименьший разброс от линейной зависимости имеют две последние из трех. Этот результат адекватен исследуемому процессу как процессу логистическому, т.е. роста с насыщением.
. Среди этих трех показателей, по-видимому, наименьший разброс от линейной зависимости имеют две последние из трех. Этот результат адекватен исследуемому процессу как процессу логистическому, т.е. роста с насыщением.
Оценивание параметра d модели АРИСС (p, d, q) основывается на следующем условии:
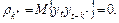 (9.24)
(9.24)
Если условие (9.24) выполняется, то порядок разностей (d), включенных в модель АРИСС (p, d, q), полагают равным 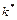 .
.
Рисунки графиков рядов и характеристик прироста:
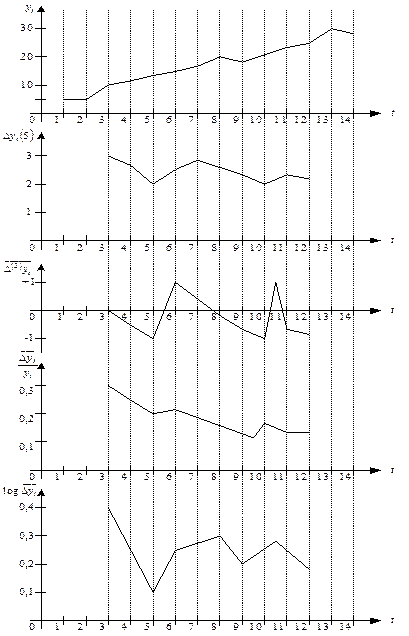
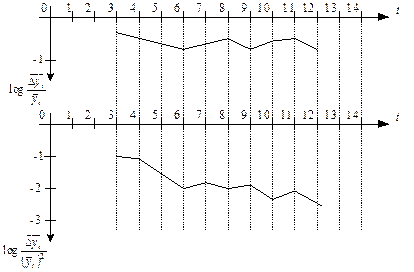
Рис. 26
Процесс преобразования исходного ряда к стационарному можно изобразить в виде графика-коррелограммы (рис. 27):

Рис. 27
Для нахождения параметров 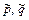 и коэффициентов модели
и коэффициентов модели 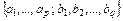 используют условие
используют условие
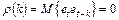 , (9.25)
, (9.25)
где 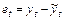 – остатки оценивания модели по взвешенному МНК.
– остатки оценивания модели по взвешенному МНК.
В табл. 9.6 описаны признаки выбора порядков p и q модели АРИСС низких порядков:
Таблица 9.6
| № | Модели | 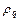
| 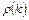
|
| 1 | АРИСС (1, 0, 0):
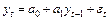
| Стремится к нулю | Обращается в нуль 1-ого лага |
| 2 | АРИСС (2, 0, 0):
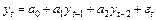
| Стремится к нулю | Обращается в нуль 2-ого лага |
| 3 | АРИСС (0, 0, 1):
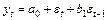
| Обращается в нуль 1-ого лага | Стремится к нулю |
| 4 | АРИСС (0, 0, 2):
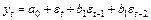
| Обращается в нуль 2-ого лага | Стремится к нулю |
| 5 | АРИСС (1, 0, 1):
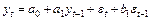
| Обращается в нуль 1-ого лага | Обращается в нуль 1-ого лага |
Для решения задачи прогноза временного ряда применяют модель с наблюдаемыми остатками 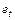 :
:
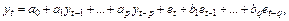
где 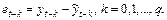
Процесс прогнозирования осуществляется последовательно, начиная с 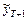 , далее
, далее 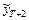 и т.д.
и т.д.
Например, для прогнозирования по модели АРИСС (2, 0, 1):
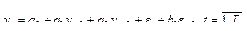
Шаг 1. Оценивают коэффициенты 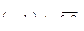 их подстановка дает:
их подстановка дает:
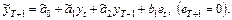
Шаг 2. Далее 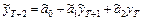 , т.е. процесс скользящего среднего уже не участвует в прогнозировании. По рекомендациям, принятым в [2], не существует универсального метода прогнозирования, его выбор зависит от:
, т.е. процесс скользящего среднего уже не участвует в прогнозировании. По рекомендациям, принятым в [2], не существует универсального метода прогнозирования, его выбор зависит от:
а) глубины прогнозирования 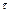 : если
: если 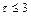 , считают прогноз краткосрочным; если
, считают прогноз краткосрочным; если 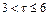 – среднесрочным; если
– среднесрочным; если 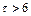 – долгосрочным;
– долгосрочным;
б) длины T наблюдаемого временного ряда (при 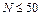 ряд классифицируется как короткий, если
ряд классифицируется как короткий, если 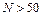 – длинный);
– длинный);
в) наличия в анализируемом временном ряду сезонной составляющей и значительной случайной («шоковой») составляющей.
Приведем простейшие примеры нахождения статистического прогнозирования в задачах кратко- и среднесрочного прогноза. Попытки построения долгосрочных корректных прогнозов обречены на неудачу без привлечения экспертных оценок.
1) Рассмотрим модель временного ряда с постоянным трендом:

1.1) Метод скользящего среднего строит прогноз вида
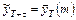 , где
, где 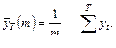
1.2) Методом экспоненциального сглаживания Брауна
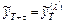 , где
, где 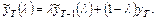
Здесь экспоненциально-взвешенная скользящая средняя 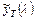 с параметром сглаживания
с параметром сглаживания 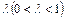 вычисляется по формуле:
вычисляется по формуле:
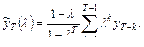
2) Для модели с линейным трендом:
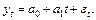
2.1) Прогноз по методу скользящей средней:
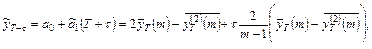
где 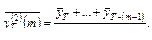
Здесь 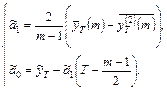
2.2) Прогноз по методу экспоненциального сглаживания:
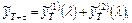
где 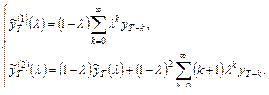
Дата добавления: 2019-11-25; просмотров: 161; Мы поможем в написании вашей работы! |

Мы поможем в написании ваших работ!
