Классификация движений жидкостей

⇐ ПредыдущаяСтр 2 из 2

На уровне физически бесконечно малых объёмов выделяют три вида движения жидкости: поступательное, вращательное и деформационное.

Из этого следует, что движение жидкости отличается от движения твёрдого тела наличием деформационного движения, вызванного изменением формы (деформацией) элементарных объёмов жидкости при движении.

Таким образом, жидкие частицы, двигаясь поступательно, одновременно вращаются и деформируются.

Если гидромеханические величины 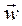, P, 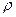, в каждой точке рассматриваемого объёма не зависят от времени, такое движение называется стационарным или установившимся.

В противном случае движение называется нестационарным (неустановившимся).

Кроме упомянутых выше, существуют и другие классификации движений, из которых для данного курса наиболее важным является подразделение движений на ламинарное и турбулентное.

При таком подразделении движений рассматривается течение макрообъёмов жидкостей.

Ламинарное течение характеризуется строго упорядоченным перемещением слоёв жидкостей параллельно друг другу в направлении течения. Ламинарное движение характерно для вязких жидкостей и движения разных жидкостей в тонких слоях и каналах (капиллярах). Оно имеет место также при обтекании жидкостью тел малых размеров.

Жидкость также движется ламинарно в слоях, расположенных близко к твёрдым поверхностям, хотя вдали от этих поверхностей ламинарного течения не наблюдается (поток турбулентный).

Ламинарное течение гидродинамически неустойчиво. При потере устойчивости оно переходит в турбулентное.

В отличие от ламинарного, турбулентное течение неупорядоченно. В турбулентных потоках образуются многочисленные вихри разных размеров, нестационарно перемещающиеся по сложным траекториям.

Вследствие этого наблюдаются хаотические флуктуации гидромеханических величин (скорости, давления, плотности).

В природе и технике жидкости в основном текут турбулентно (вода в реках и океанах, воздух в атмосфере, жидкости в трубах и каналах, в струях). Хаотически перемещающиеся вихри вызывают интенсивное перемешивание по поперечному сечению потока, что приводит к ускорению переноса импульса тепла и массы, поэтому турбулентное течение характерно для теплообменных и массообменных процессов.

Переход ламинарного течения в турбулентное характеризуется определенным (критическим) значением безразмерного комплекса величин, называемым критерием (числом) Рейнольдса, определяемым по формуле

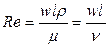(5)

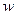где: и 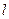- характерные величины скорости и длины в рассматриваемом течении.

При течении в трубах и каналах, характерными величинами являются средняя скорость в поперечном сечении трубы (канала) и эквивалентный диаметр ( d э).

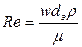(6)

Эквивалентный диаметр канала определяется по формуле

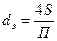(7)

где: S – площадь поперечного сечения потока в канале, м2

П -смоченный периметр канала, м.

Формула показывает, что эквивалентный диаметр канала равен диаметру виртуального круга, имеющего те же значения S и П.

Иногда в качестве характерного размера используют так называемый гидравлический радиус

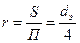(8)

Экспериментальное критическое значение числа Рейнольдса, соответствующее переходу ламинарного течения в турбулентное в прямых круглых трубах при наибольшей возможной возмущенности течения у входа в трубу:

Re кр = 2300

При уменьшении возмущенности течения на входе можно добиться увеличения Re кр до 50 000.

В технике течение в трубах считается устойчивым ламинарным при Re < 2300.

В области 2300 < Re < 10 000движение является неустойчивым турбулентным и при Re ³ 10 000 течение устойчивое турбулентное.

ПОЛЕ СКОРОСТЕЙ

В технической гидромеханике для описания движения жидкости используется метод Эйлера, согласно которому анализируется изменение гидромеханических величин в неподвижных точках пространства с течением времени. При этом рассматривается перемещение жидкой частицы за время dt на расстояния dx, dy, dz. В конечном итоге задачей кинематики и гидродинамики по методу Эйлера является определение функций:

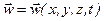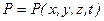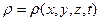, , (9)

Иначе говоря, определяется векторное поле скоростей и скалярные поля давления и плотности.

При анализе течения жидкости используют понятие линии тока, которая представляет собой линию в области движения жидкости, касательная к которой в каждой точке в данный момент времени совпадает с направлением скорости.

Для установившегося движения линии тока совпадают с траекториями движения частиц, которые определяются из системы уравнений:

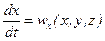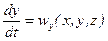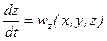, , (10)

где 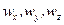– компоненты вектора скорости .

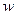При неустановившемся движении компоненты скорости будут зависеть также от времени. В этом случае линии тока совпадают с траекториями в том случае, если направление скорости постоянно во времени.

ГИДРОДИНАМИКА.

Уравнения движения жидкости

Уравнения гидродинамики являются следствием фундаментальных законов сохранения массы, импульса и энергии.

Уравнение неразрывности

Составим материальный баланс неразрывного (сплошного) течения жидкости.

Рассмотрим в области течения произвольный объём V, ограниченный поверхностью S (Рис.2).

Рис.2. К выводу уравнения

неразрывности

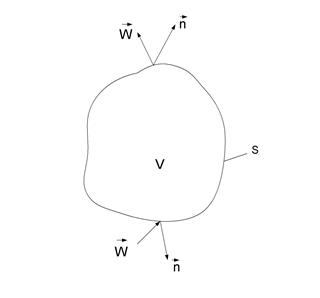В каждой точке этой поверхности проведём единичную нормаль 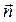. Будем считать, что источники массы внутри объёма V отсутствуют. Объёмный поток жидкости (расход) входящий в рассматриваемую область из жидкости, примыкающей к данному объёму, т.е. приток жидкости снаружи:

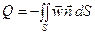(11)

Знак (-) в уравнении делает входящие потоки положительными.

Массовый поток найдём, умножив подинтегральное выражение на плотность

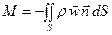M = [кг/с] (12)

Произведение 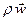называют массовой скоростью или плотностью массового потока.

Интеграл поверхности по формуле Остроградского-Гаусса преобразуем в интеграл по объёму

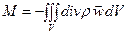(13)

Найдём то же изменение массы жидкости в единицу времени, рассматривая объём V изнутри

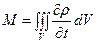
Приравнивая потоки, полученные определением притока массы снаружи и изнутри объёма V получим

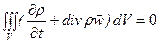(14)

Поскольку для произвольного объёма подинтегральная функция должна обращаться в нуль, получим уравнение неразрывности (сплошности)

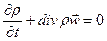(15)

Уравнение неразрывности является законом сохранения массы в дифференциальной форме. Для стационарного движения 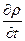=0, поэтому уравнение (15) принимает вид

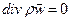(16)

Если жидкость несжимаема 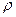= с onst, следовательно

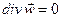(17)

Запишем это уравнение для компонентов скорости

(17а)

Записав 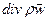в развёрнутой форме, из уравнения (15) получаем

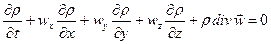
Это уравнение можно записать в следующем виде

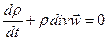(18)

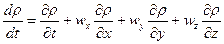где (19)

Величина 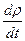называется индивидуальной (т.е. взятой для конкретной жидкой частицы) или субстанциональной производной.

Раскроем физический смысл индивидуальной производной.

Поскольку по методу Эйлера мы следим за изменением любой гидромеханической величины при прохождении жидкой частицы за время dt расстояний dx , dy , dz , то полный дифференциал плотности равен

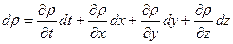, (20)

следовательно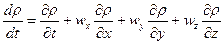

где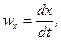

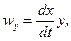
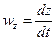
Первое слагаемое уравнения (20) означает изменение плотности в данной фиксированной (неподвижной) точке пространства в течение времени dt , а остальные слагаемые дают изменение 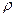за счёт перемещения частицы на расстояния dx , dy , dz.

Индивидуальная производная в форме уравнения (19) может быть записана для любой скалярной или векторной величины 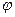(плотности, давления, скорости):

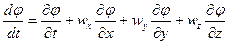(21)

Частную производную 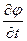также называют местной производной (т.е. для некоторой неподвижной в пространстве точки).

Из уравнения (21) можно также заключить, что - для нестационарного процесса 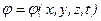, - для стационарного ( )

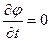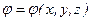
Получаем уравнение неразрывности в интегральной форме для стационарного течения жидкости.

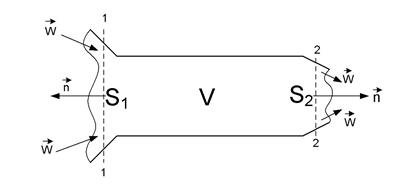Рассмотрим стационарное неразрывное течение жидкости в канале произвольной формы с непроницаемыми стенками (Рис.3).

Рис.3. К выводу уравнения неразрывности в интегральном виде

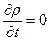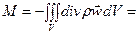
Запишем уравнения материального баланса (ур. 12-14) при , для части канала, ограниченной плоскими сечениями 1 и 2 с поверхностями S 1 и S 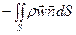2

(22)

Поскольку стенки непроницаемые, имеем равенство

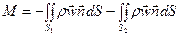(23)

Найдём положительные величины средней массовой скорости для сечений 1 и 2

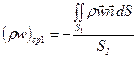
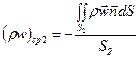(24)

Из уравнений (23) и (24) получим уравнение неразрывности в интегральной форме

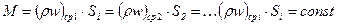(25)

В случае, когда плотность не меняется по сечению, имеем

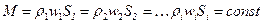(26)

где 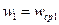, 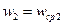и т.д.

Для несжимаемой жидкости

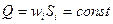(27)

Уравнения (25-27) служат для определения скоростей жидкости и площадей сечений каналов.

Дата добавления: 2019-11-25; просмотров: 627; Мы поможем в написании вашей работы!

Поделиться с друзьями:

⇐ Предыдущая 12

Мы поможем в написании ваших работ!