Нахождение приближенного значения корня нелинейного уравнения

Цели:

ü познакомиться с алгоритмаминахождения приближенного значения корня нелинейного уравнения на заданном отрезкес заданной точностью;

ü методику написания и перевода таких алгоритмов на язык программирования С++ и разработки соответствующего проекта в среде Visual C++ 6.0.

Нелинейные уравнения – это уравнения, в которые переменная входит в степени больше чем 1. Решить уравнение – значит, найти его корень. Корнем называется такое значение переменной, при подстановке которого в уравнение вместо переменной уравнение превращается в верное равенство.

1. Методы нахождения корней уравнения f ( x )=0

на отрезке [ a ; b ] с заданной точностью eps

Постановка задачи заключается в следующем. Дан отрезок [a;b], на котором находится корень уравнения f(x)=0. Найти с заданной точностью eps корень этого уравнения. Рассмотрим три метода нахождения корней нелинейных уравнений.

Метод дихотомии (половинного деления)

Данный метод основывается на утверждении, что если на отрезке [a;b] содержится корень уравнения, то значения f(a) и f(b) имеют разные знаки, т.е. f(a)·f(b)<0.

Схема метода

Отрезок делится пополам – середина обозначается через точку c (рис.14). Если |a-b|>=eps, то вычисле-ния продолжаются. Эта проверка означает, что если |a-b|<eps, то длина отрезка, на котором находится корень уравнения, достаточна мала и вычисления можно прекратить, а за значение корня можно взять середину этого отрезка, т.е. корень уравнения вычислен с заданной точность eps. Происходит проверка f(a)·f(c)<0 или нет. Если да, то значение c присваивается перемен-ной b, иначе значение c присваива-ется переменной a. Если |a-b|>=eps, то опять происходит проверка f(a)·f(c)<0 или нет. Если да, то значение c присваивается переменной b, иначе значение c присваивается перемен- ной a и т.д. Графически этот метод изображен на рис.14.

Опишем алгоритм и соответствующую программу для нахождения корней уравнения ln(x-3)=0 на отрезке [3.5;5] с помощью этого метода:

Алгоритм

Программа

объявление вещ: fa, fb, fc, a, b, c, eps ввод а ввод b fa=ln(a-3) fb=ln(b-3) если fa*fb<0 ввод eps c=(a+b)/2 fc=log(c-3) пока (|a-b|>=eps ) если (fa*fc<0) b=c иначе a=c; всё если c=(a+b)/2 fa=ln(a-3) fb=ln(b-3) fc=ln(c-3) всё пока печать c печать fc иначе печать “на отрезке нет корня” все_если

#include "stdio.h" #include "math.h" #include "iostream.h" #include "iomanip.h" int main() { float fa, fb, fc, a, b, c, eps; cout<<"a="; cin>>a; cout<<"b="; cin>>b; fa=log(a-3); fb=log(b-3); if(fa*fb<0) { cout<<"eps="; cin>>eps; c=(a+b)/2; fc=log(c-3); while(fabs(a-b)>=eps) { if(fa*fc<0) b=c; else a=c; //вычисляется новая середина //отрезка c=(a+b)/2; //вычисляются значения //функций в новых точках fa=log(a-3); fb=log(b-3); fc=log(c-3); } cout<<"корень уравнения х*="<<c<<endl; cout<<"значение f(x*)="<<fc<<endl; } else cout<<"неверно введены концы" <<"отрезка"<<endl; return 1; }

Метод хорд

Метод основывается на утверждении, что если на отрезке [a;b] содержится корень уравнения, то значения f(a) и f(b) имеют разные знаки, т.е. f(a)·f(b)<0.

Схема метода аналогична предыдущему. Разница заключается в поиске значения точки c. Для этого в методе хорд используется уравнение хорды – прямой, проходящей через две точки некоторой кривой. Возьмём т.А(a;f(a)) и т.B(b;f(b)) на кривой y=f(x). Уравнение прямой проходящей через эти точки . Пусть первая координата т.С(с;0) – корень уравнения f(x)=0. Подставим координаты точки C в полученное уравнение. В итоге получаем уравнение для получения значений точек с_i при вычислении корня исходного уравнения:

Вычисляется точка c. Если |a-b|>=eps, то вычисления продолжаются. Эта проверка означает, что если |a-b|<eps, то длина отрезка, на котором находится корень уравнения, достаточна мала и вычисления можно прекратить, а за значение корня взять один из концов этого отрезка, т.е. корень уравнения вычислен с заданной точность eps. Происходит проверка f(a)·f(c)<0 или нет. Если да, то значение c присваивается переменной b, иначе значение c присваивается переменной a, т.е. исходный отрезок суживается. Если |a-b|>=eps, то опять происход-ит проверка f(a)·f(c)<0 или нет. Если да, то значение c присваивается переменной b, иначе значение c присваивается переменной a и т.д. Графически этот метод изображен на рис.15.

Алгоритм

Программа

объявление вещ: fa, fb, fc, a, b, c, eps ввод а ввод b fa=ln(a-3) fb=ln(b-3) если fa*fb<0 ввод eps c=а-(b-a)*fa/ (fb-fa) fc=log(c-3) пока (|a-b|>=eps ) если (fa*fc<0) b=c иначе a=c; всё если c=а-(b-a)*fa/ (fb-fa) fa=ln(a-3) fb=ln(b-3) fc=ln(c-3) всё пока печать c печать fc иначе печать “на отрезке нет корня” все_если

#include "stdio.h" #include "math.h" #include "iostream.h" #include "iomanip.h" int main() { float fa, fb, fc, a, b, c, eps; cout<<"a="; cin>>a; cout<<"b="; cin>>b; fa=log(a-3); fb=log(b-3); if(fa*fb<0) { cout<<"eps="; cin>>eps; c= а-(b-a)*fa/ (fb-fa); fc=log(c-3); while(fabs(a-b)>=eps) { if(fa*fc<0) b=c; else a=c; //вычисляется новое значение с c=а-(b-a)*fa/ (fb-fa); //вычисляются значения //функций в новых точках fa=log(a-3); fb=log(b-3); fc=log(c-3); } cout<<"корень уравнения х*="<<c<<endl; cout<<"значение f(x*)="<<fc<<endl; } else cout<<"неверно введены концы" <<"отрезка"<<endl; return 1; }

Метод касательных (Ньютона)

Метод основывается на утверждении, что если на отрезке [a;b] содержится корень уравнения, то значения f(a) и f(b) имеют разные знаки, т.е. f(a)·f(b)<0. Точность вычислений зависит от выбора точки, с которой начинаются вычисления. Выбор начальной точки x₀ вычислений определяет условие 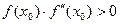. Схема метода аналогична предыдущим. Разница заключается в поиске значения точки c. Для этого в методе касательных используется уравнение касательной к графику функции: 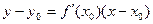. Пусть первая координата т.С(с_i;0) – корень уравнения f(x)=0. Подставим координаты точки C в полученное уравнение. В итоге получаем уравнение для получения значений точек с_i при вычислении корня исходного уравнения:

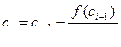Если |c_i-c_i_-1|>=eps, то вычисления продолжаются. Если |c_i-c_i_-1|<eps, то вычисления можно прекратить, а за значение корня взять одно из этих значений, т.е. корень уравнения вычислен с заданной точность eps. Если нет, то вычисляется новое значение с_i и т.д. Графически этот метод изображен на рис.16.

Алгоритм

Программа

объявление вещ: f_2p, fa, fb, a, b, c, c1, eps ввод а ввод b fa=ln(a-3) fb=ln(b-3) если fa*fb<0 ввод eps f_2p=-1/(a-3)² если fa*f_2p>0 c1=a иначе c1=b все_если c=c1-ln(c1-3)/(1/(c1-3)) пока (|c-c1|>=eps ) c1=c c=c1-ln(c1-3)/(1/(c1-3)) всё_цикл печать c печать ln(c-3) иначе печать “на отрезке нет корня” все_если

#include "stdio.h" #include "math.h" #include "iostream.h" #include "iomanip.h" int main() { float f_2p, fa, fb, a, b, c, c1, eps; cout<<"a="; cin>>a; cout<<"b="; cin>>b; fa=log(a-3); fb=log(b-3); if(fa*fb<0) { cout<<"eps="; cin>>eps; f_2p=-1/pow(a-3,2); if(fa*f_2p>0) c1=a; else c1=b; c=c1-log(c1-3)/(1/(c1-3)); while(fabs(c-c1)>=eps) { c1=c; c= c1-log(c1-3)/(1/(c1-3)); } cout<<"корень уравнения х*="; cout<<c<<endl; cout<<"значение f(x*)="<<log(c-3)<<endl; } else cout<<"неверно введены концы" <<"отрезка"<<endl; return 1;}

Л екция 21

Дата добавления: 2019-11-25; просмотров: 189; Мы поможем в написании вашей работы!

Поделиться с друзьями:

⇐ Предыдущая 14 15 16 17 181920 21 22 23 Следующая ⇒

Мы поможем в написании ваших работ!