Значення похідної в деякій точці дорівнює тангенсу кута, утвореного дотичною до кривої в цій точці з додатним напрямом осі Ох.
ЛЕКЦІЯ
 |
ПОХІДНА
ТА ЇЇ ЗАСТОСУВАННЯ
13.1. Відомості з історії
1. Про походження термінів і позначень. Розділ математики, в якому вивчаються похідні та їх застосування до дослідження функцій, називається диференціальним численням. Приріст виду 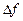 , що являє собою різницю, відіграє помітну роль під час роботи з похідними. Тому цілком природною видається поява латинського кореня differentia (різниця) у назві calculis differentialis зазначеного числення, що з’явилося наприкінці XVII століття.
, що являє собою різницю, відіграє помітну роль під час роботи з похідними. Тому цілком природною видається поява латинського кореня differentia (різниця) у назві calculis differentialis зазначеного числення, що з’явилося наприкінці XVII століття.
Термін «похідна» є буквальним перекладом на українську французького терміна derivée, що його ввів 1797 року Ж. Лагранж (1736—1813); він же впровадив сучасні позначення 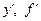 . Така назва відбиває зміст поняття: функція
. Така назва відбиває зміст поняття: функція 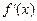 походить від
походить від 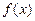 , є похідною від
, є похідною від 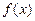 . Ньютон називав похідну функцію флюксією, а саму функцію — флюентою. І. Г. Лейбніц говорив про диференціальне відношення і ввів позначення похідної
. Ньютон називав похідну функцію флюксією, а саму функцію — флюентою. І. Г. Лейбніц говорив про диференціальне відношення і ввів позначення похідної 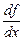 , яке також часто зустрічається в сучасній літературі.
, яке також часто зустрічається в сучасній літературі.
Символ 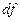 Лейбніц вибрав для позначення диференціала функції
Лейбніц вибрав для позначення диференціала функції 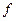 . (Диференціал
. (Диференціал 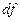 функції
функції 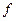 — це добуток похідної
— це добуток похідної 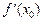 на приріст
на приріст 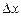 , тобто
, тобто 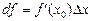 ; замінюючи позначення
; замінюючи позначення 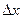 на
на 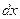 , це можна записати так:
, це можна записати так: 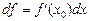 , звідки
, звідки 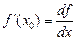 ). Теоретичний зміст диференціалу стає зрозумілим із розгляду рис. 1:
). Теоретичний зміст диференціалу стає зрозумілим із розгляду рис. 1: 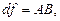
 — дотична до графіку.
— дотична до графіку.
Розповідь про походження термінології, прийнятої в диференціальному численні, була б неповною без поняття границі і нескінченно малої. Більш ретельно про це поговоримо далі, а поки зауважимо, що похідні визначається як границя:
|
|
|
Похідною функції 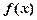 у точці х0 називають границю, до якої прямує відношення приросту функції до приросту аргументу коли останній прямує до нуля:
у точці х0 називають границю, до якої прямує відношення приросту функції до приросту аргументу коли останній прямує до нуля:
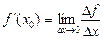 .
.
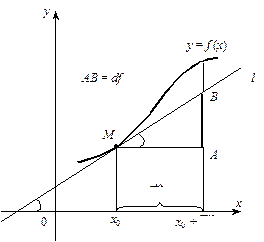
Рис. 1
Позначення 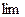 — скорочення латинського слова limes (межа, границя); зменшуючи, наприклад,
— скорочення латинського слова limes (межа, границя); зменшуючи, наприклад, 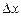 , ми спрямовуємо значення
, ми спрямовуємо значення 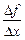 до границі
до границі 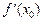 . Термін «границя» увів Ньютон.
. Термін «границя» увів Ньютон.
Прикладом нескінченно малої може бути функція 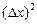 від
від 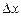 , оскільки
, оскільки 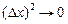 при
при 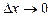 . Узагалі, якщо
. Узагалі, якщо 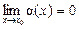 , говорять, що
, говорять, що 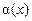 — нескінченно мала. Нескінченно малі відіграють важливу роль у математичному аналізі, який з огляду на це часто називають також аналізом нескінченно малих.
— нескінченно мала. Нескінченно малі відіграють важливу роль у математичному аналізі, який з огляду на це часто називають також аналізом нескінченно малих.
Зауважимо нарешті, що слово «екстремум» походить від латинського extremum (крайній). Maximum перекладається як найбільший, а minimum — найменший.
2. З історії диференціального числення. Диференціальне числення було створено Ньютоном і Лейбніцем порівняно недавно, наприкінці XVII сторіччя. Проте вражає той факт, що задовго до цього Архімед не тільки розв’язав задачу на побудову дотичної до такої складної кривої, як спіраль (застосувавши при цьому граничні переходи), а й зумів знайти максимум функції  .
.
|
|
|
Епізодично поняття дотичної (яке також пов’язане з поняттям похідної) зустрічалося у працях італійського математика Н. Тартальї (бл. 1500—1557) — тут дотична з’явилася в ході вивчення питання про кут нахилу гармати, при якому забезпечується найбільша дальність польоту снаряда. Й. Кеплер розглядав дотичну, розв’язуючи задачу про найбільший об’єм паралелепіпеда, уписаного в кулю даного радіуса.
У XVII столітті на основі вчення Г. Галілея про рух активно розвинулася кінематична концепція похідної, передусім у працях Р. Декарта, французького математика Роберваля (1602—1675), англійського вченого Д. Грегорі (1638—1675), у працях Й. Барроу (1630—1677) і, нарешті, І. Ньютона.
До розгляду дотичної і нормалі (так називається пряма, перпендикулярна до дотичної в точці дотику) Декарт прийшов під час вивчення оптичних властивостей лінз. За допомогою методів аналітичної геометрії та винайденого ним методу невизначених коефіцієнтів Декарт зумів розв’язати задачі про побудову нормалей до ряду кривих, зокрема еліпса.
У 1629 році П. Ферма запропонував правила відшукання екстремумів многочленів, застосовуючи граничні переходи.
Ферма відіграв видатну роль у розвитку математики. Його ім’ям названо одну з найвідоміших теорем теорії чисел — велику теорему Ферма, яку не доведено й досі. Ферма — один із творців аналітичної геометрії. Він займався й оптикою, сформулювавши широко відомий фундаментальний принцип: промінь світла поширюється так, що час його проходження найменший.
|
|
|
Важливим наслідком цього принципу є, наприклад, закон відбиття світла: кут відбиття дорівнює куту падіння. Те саме стосується закону заломлення світла на межі поділу двох різних за густиною однорідних середовищ.
Зауважимо, що методи Ферма, що стосуються відшукання максимумів і мінімумів, побудови дотичних, обчислення площ — важливі віхи в передісторії диференціального та інтегрального числення.
Систематичне вчення про похідні розвинули Лейбніц та І. Ньютон, що мало величезний вплив на подальший розвиток математики та природознавства.
Якщо Ньютон виходив передусім із задач механіки (ньютонів аналіз створювався одночасно з ньютоновою класичною механікою), то Лейбніц розглядав переважно геометричні задачі.
Говорячи про подальший розвиток ідей аналізу (а вони дуже швидко завоювали популярність і знайшли багатьох послідовників), слід насамперед назвати імена учнів Лейбніца — братів Якоба та Йога Бернуллі.
|
|
|
А. Лопіталь (1661—1704) — учень Й. Бернуллі, уже 1696 року видав перший друкований курс диференціального числення «Аналіз нескінченно малих для дослідження кривих ліній», що сприяв поширенню нових методів.
Чимало вагомих результатів здобув Лагранж, праці якого відіграли важливу роль в осмисленні основ аналізу.
Неоціненний внесок у розвиток математичного аналізу, як і багатьох інших розділів математики, зробили Л. Ейлер і К. Ф. Гаус (1777—1855).
У стислому огляді неможливо розповісти про суть відкриттів у галузі математичного аналізу, зроблених у XVIII столітті та в наступні роки. Але про один напрямок не можна не згадати. Ідеться про розкладання функцій у степеневі ряди, тобто про подання функцій у вигляді многочленів із нескінченною кількістю доданків. Прикладом нескінченної суми (числового ряду) в елементарній математиці є нескінченні періодичні дроби, що подаються у вигляді суми нескінченної кількості доданків. З числовими та функціональними рядами працював не тільки Ньютон, але і його попередники, і тому не зовсім справедливо, що чудове співвідношення
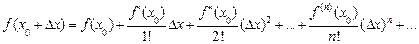
( 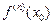 — значення, здобуте в результаті n-кратного диференціювання функції
— значення, здобуте в результаті n-кратного диференціювання функції 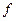 у точці
у точці 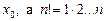 ) названо формулою Тейлора. (Б. Тейлор (1685—1731) — англійський математик, який опублікував її в 1715 році),
) названо формулою Тейлора. (Б. Тейлор (1685—1731) — англійський математик, який опублікував її в 1715 році),
З’ясувалося, що нерідко, відкидаючи нескінченну кількість доданків, можна діставати формули, що дають прийняті наближення функцій многочленами.
Зауважимо, що ентузіазм, викликаний появою нового могутнього методу математики, який дає змогу розв’язувати широке коло практичних задач, сприяв бурхливому розвитку аналізу у XVIII столітті. Але вже до кінця цього століття проблеми, з якими стикнулися творці диференціального та інтегрального числення, постали дуже гостро.
Основні труднощі полягали в тому, що не було сформульовано точних означень таких ключових понять, як «границя», «неперервність», «дійсне число». Через це й відповідні міркування містили логічні прогалини, а іноді були навіть помилковими. Характерний приклад — визначення неперервності. Ейлер, Лагранж і навіть Фур’є (а він працював уже на початку XIX століття) називали неперервною функцію, задану у своїй області визначення одним аналітичним виразом.
Тим самим «нова» математика не відповідала стандартам строгості, звичним для вчених, вихованих на класичних зразках грецьких математиків. Інтуїція, конче потрібна математикам, істотно випередила логіку, що також є невід’ємною характеристикою математичної науки.
Геніальна інтуїція таких гігантів, як Ньютон, Лейбніц, Ейлер, допомагала їм уникати помилок. Але необхідно було створювати міцні логічні основи.
Із цього приводу згадаймо характерні висловлення тогочасних мислителів. Відомий математик М. Ролль писав, що нове числення є колекцією геніальних помилок. А великий французький філософ Вольтер зазначав, що це числення являє собою мистецтво обчислювати і точно вимірювати речі, існування яких не може бути доведено.
Рішучий крок до створення міцного фундаменту аналізу зробив у 20-х роках XIX століття французький математик О. Коші (1789—1857), запропонувавши точні означення границі функції та послідовності і на їх основі довівши багато принципових теорем аналізу. Дещо раніше (1821 р.) означення границі та неперервності функції, багато інших важливих результатів (зокрема, знаменитий приклад функції, неперервної на проміжку, яка не має похідної в жодній його точці) подав чеський математик Б. Больцано (1781—1848), але його праці стали відомими значно пізніше.
Означення границі функції за Коші формулюється так: число 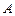 називається границею функції
називається границею функції 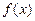 при
при  , що прямує до
, що прямує до 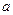 (записують
(записують 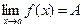 ), якщо для довільного числа
), якщо для довільного числа 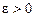 можна знайти таке число
можна знайти таке число 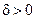 , що
, що 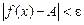 для всіх
для всіх  , які задовольняють нерівність
, які задовольняють нерівність 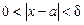 .
.
Спираючись на це означення, уже неважко дати означення неперервності функції в точці: функція 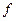 неперервна в точці
неперервна в точці 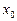 , якщо
, якщо 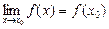 .
.
Означення границі послідовності за Коші аналогічне: число 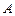 є границею послідовності
є границею послідовності 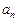 , якщо для кожного
, якщо для кожного 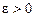 існує номер
існує номер 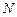 , такий що при усіх
, такий що при усіх 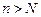 справджується нерівність
справджується нерівність 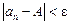 .
.
Коші довів формульовані далі теореми про границі, якими ми фактично користуємося при обчисленні похідних:
Якщо 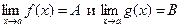 , то існують границі суми, різниці, добутку та частки (при
, то існують границі суми, різниці, добутку та частки (при 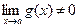 ) цих функцій, обчислювані за такими правилами:
) цих функцій, обчислювані за такими правилами:
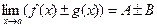 ,
,
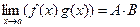 ,
,
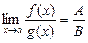 .
.
(1)
Гасло багатьох математиків XVII століття було таке: «Рухайтеся вперед — і віра в правильність результатів до вас прийде».
13.2. Похідна
Поняття похідної
Нехай у = f (x) — неперервна функція аргументу х, визначена на інтервалі (a, b). Візьмемо деяке значення незалежної змінної х і надамо їй деякого приросту Dх. Тоді функція y = f(x) набуде приросту (рис. 1)
Dу = f(x + Dx) – f(x).
Відношення 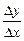 приросту Dу функції у = f(x) до приросту
приросту Dу функції у = f(x) до приросту 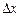 незалежної змінної х називається диференціальним відношенням:
незалежної змінної х називається диференціальним відношенням:
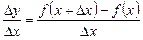 . (1)
. (1)
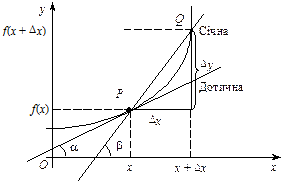
Рис. 2
Відношення 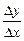 — це тангенс кута нахилу січної до осі Ох. При
— це тангенс кута нахилу січної до осі Ох. При 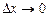 січна прямує до дотичної в точці Р. Тангенсом кута a нахилу дотичної до осі Ох при цьому буде границя відношення
січна прямує до дотичної в точці Р. Тангенсом кута a нахилу дотичної до осі Ох при цьому буде границя відношення
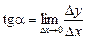 .
.
Функція у = f(x) називається диференційовною в точці х = х0, якщо існує границя
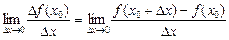 . (2)
. (2)
Значення границі при цьому називається похідною функції
у = f(x) у точці х0 і позначається
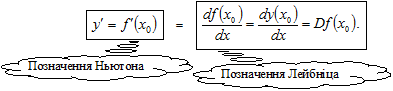
Функція називається диференційовною на інтервалі І, якщо вона диференційовна в кожній точці х цього інтервалу.
Кожному значенню х із області диференційовності функції f (x) ставиться у відповідність її похідна в точці х. Отже, дістаємо похідну функцію, яку позначаємо f¢ (x). Дія відшукання похідної функції f (x) називається диференціюванням.
Приклад. Розглянемо функцію 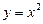 і знайдемо диференціальне відношення та похідну цієї функції (рис. 2).
і знайдемо диференціальне відношення та похідну цієї функції (рис. 2).
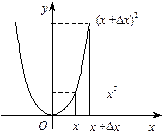
Рис. 2
Ø Диференціальне відношення визначаємо за формулою (1):
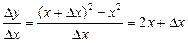 .
.
Похідну знаходимо за (2):
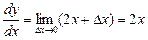 .
.
Похідні основних
елементарних функцій
1. Похідна степеневої функції у = х a :
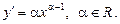
2. Похідна показникової функції у = ах:
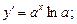
зокрема, при у = ех:
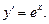
3. Похідна логарифмічної функції 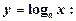
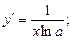
зокрема, при 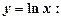
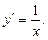
4. Похідні тригонометричних функцій:
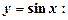
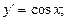
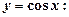
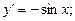
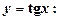
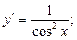
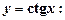
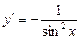 .
.
Правила диференціювання
ПРАВИЛО 1. Похідна сталої дорівнює нулю:
(сonst)¢ = 0.
Приклад. (7)¢ = 0; (– 100)¢ = 0.
ПРАВИЛО 2. Якщо u — будь-яка диференційовна функція від х і с — довільна стала, то (cu) ¢ = cu¢.
Приклад. Ø 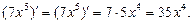
ПРАВИЛО 3. Якщо u та v — диференційовні функції від х, то їхня сума u + v є диференційовною функцією:
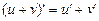 .
.
Аналогічно, похідна суми будь-якої скінченної кількості диференційовних функцій дорівнює сума похідних даних функцій:
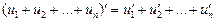 .
.
Приклад. Знайти похідну функції 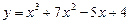 .
.
Ø 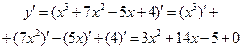 .
.
ПРАВИЛО 4. добуток двох диференційовних функцій u та v є диференційовною функцією:
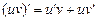 .
.
Похідна добутку n функцій:
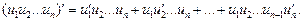 (3)
(3)
Приклад. Знайти у¢, якщо у = (х2 +1) lnx.
Ø 
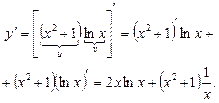
ПРАВИЛО 5. У точках, в яких 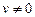 , відношення
, відношення 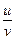 двох диференційовних функцій є функція диференційовна, причому
двох диференційовних функцій є функція диференційовна, причому
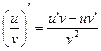 .
.
Приклад. Знайти у¢, якщо 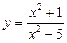 .
.
Ø 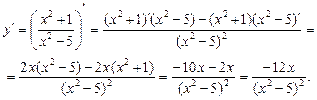
Похідна оберненої функції
ПРАВИЛО 6. Якщо функція у = f(x) монотонна й має в точці х відмінну від нуля похідну, то функція, обернена до даної, подається у вигляді х = g(y) і має похідну х = g(y), обернену до похідної даної функції:
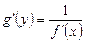 (4)
(4)
Похідні обернених тригонометричних функцій:
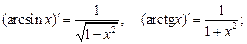
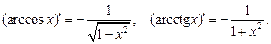
Похідна складеної функції
ПРАВИЛО 7. Похідна складеної функції 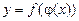 :
:
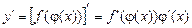 — правило ланцюга. (5)
— правило ланцюга. (5)
Приклад. Задано функцію у = f(x). Знайти у¢.
1) 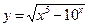 ; 2)
; 2) 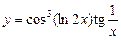 ; 3)
; 3) 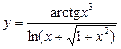 .
.
Ø За формулою (5) маємо:
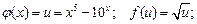
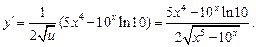
2) Візьмемо: 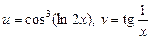 . Тоді за правилом 4 дістаємо:
. Тоді за правилом 4 дістаємо:
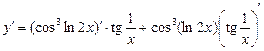 .
.
Функції 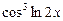 і
і 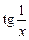 — складені. Згідно з (5) маємо:
— складені. Згідно з (5) маємо:
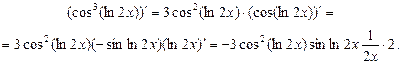
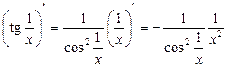 .
.
3) Нехай 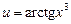 і
і 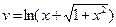 . Тоді за правилом 5 дістаємо:
. Тоді за правилом 5 дістаємо:
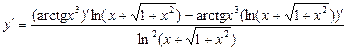 .
.
Похідні функцій arctgx3 і 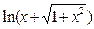 обчислюємо за формулою (5):
обчислюємо за формулою (5):
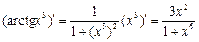 ;
;
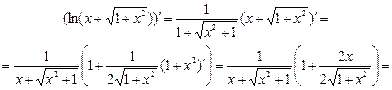
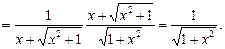 ¨
¨
Логарифмічне диференціювання
ПРАВИЛО 8. Якщо функція у = f(x) являє собою добуток кількох множників, то перш ніж диференціювати цю функцію, її можна злогарифмувати.
Приклад. Знайти у¢, якщо 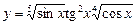 .
.
Ø Злогарифмуємо обидві частини даного рівняння:
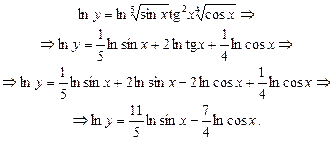
Здиференцюємо обидві частини останньої рівності:
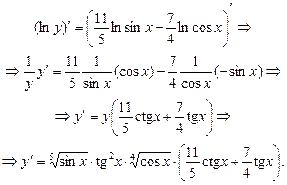
Правило диференціювання
показниково-степеневої функції
ПРАВИЛО 9. Щоб знайти похідну показниково-степеневої функції, потрібно спочатку здиференціювати її як показникову, а потім як степеневу функцію.
Окремі випадки:
1. Нехай функція y = f(x) є показниковою:
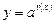 , тобто
, тобто 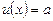 .
.
Тоді
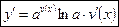 .
.
2. Нехай функція у = f(x) є степеневою, 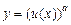 , тобто v(x) = а.
, тобто v(x) = а.
Тоді
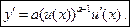
Приклад. Знайти у¢, якщо у = (х2 + 1)sinx.
Ø 1) 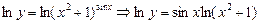 .
.
2) 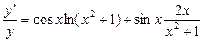 .
.
3) 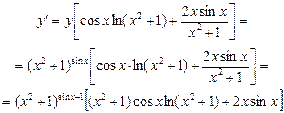
Похідні вищих порядків
Нехай у = f(x) — деяка диференційовна функція на інтервалі І, причому похідна цієї функції у ¢ = f ¢ (x) також є диференційовною функцією на зазначеному інтервалі. Похідна функції f ¢(x) називається похідною другого порядку функції f і позначається f ¢¢або f (2). Якщо f (2) диференційовна на інтервалі І, то похідна функції f (2) називається похідною третього порядку функції f (х)і позначається f (3).
Аналогічно, похідною n-го порядку f (n)функції f (х) за індукцією називається похідна функції f (n-1), якщо вона існує і диференційовна.
Іноді замість позначення f (n)(х) застосовують символ 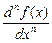 або Dny, Dnf(x).
або Dny, Dnf(x).
Приклад. Для функції f(x) = х4 + 2х3 + х + 5 знайти похідну n-го порядку.
Ø f ¢(x) = 4х3 + 6х2 + 1,
f ²(x) = 12х2 + 12х,
f (3)(x) = 24х + 12,
f (4)(x) = 24,
f (n)(x) = 0 для n ³ 5.
Правила відшукання
похідних n-го порядку
На похідні n-го порядку легко поширюються правила відшукання похідних першого порядку.
Очевидно, виконуються рівності:
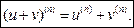
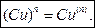
Виведемо так звану формулу Лейбніца, яка дає змогу обчислювати похідну n-го порядку від добутку двох функцій u(x) та v(x). Для того щоб вивести цю формулу, знаходимо спочатку кілька похідних, а далі встановлюємо загальне правило:
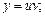
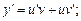
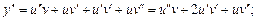
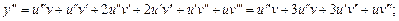
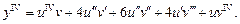
Закон утворення похідних зберігається для похідних будь-якого порядку й полягає ось у чому.
Вираз (u + v)n потрібно розкласти за формулою бінома Ньютона й у здобутому розкладі замінити показники степенів для u та v показниками порядку похідних, причому нульові степені, що входять у крайні члени розкладу, слід замінити самими функціями (тобто похідними нульового порядку):
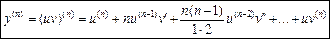
Це формула Лейбніца.
Зауваження. Повне доведення цієї формули можна подати методом повної математичної індукції [9].
Приклад. Задано функцію  . Знайти її похідну у(n).
. Знайти її похідну у(n).
Ø 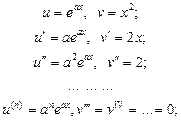
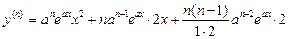 ,
,
або
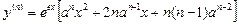 .
.
Механічний та геометричний зміст похідної
Джерелом диференціального числення стали, як відомо, два питання:
1) про відшукання швидкості в разі довільного закону руху;
2) про відшукання дотичної до довільної лінії.
Обидва вони привели до однієї й тієї самої обчислювальної задачі, яку було покладено в основу диференціального числення. Ця задача полягає в тому, щоб за даною функцією f(x) відшукати іншу функцію f ¢ (x), яка дістала назву похідної і являє собою швид кість зміни функції f(x) щодо зміни аргументу.
У механіці відповідна задача формулюється так: знайти швидкість тіла, що рухається за законом 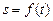 , у деякий момент часу t. Вважаємо, що відстань s і час t — фізичні величини, які можна вимірювати.
, у деякий момент часу t. Вважаємо, що відстань s і час t — фізичні величини, які можна вимірювати.
Нехай за час від t до t + Dt тіло пройшло шлях s + Ds = f(t + Dt).
Тоді Ds = f(t + Dt) – f(t).
Середня швидкість тіла, що рухається вздовж деякої лінії, визначається за формулою:
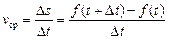 .
.
Щоб знайти миттєву швидкість v такого тіла, потрібно перейти до границі відношення 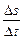 при
при 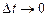 :
:
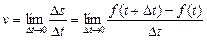 .
.
Миттєвою швидкістю тіла, що рухається вздовж лінії s = f(t), називається похідна функції s = f(t) за часом t:
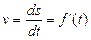 .
.
Приклад. Нехай 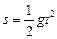 — рівняння вільного руху тіла, g — прискорення його вільного падіння. Знайти миттєву швидкість тіла в будь-який момент часу; у момент часу t = 2 c.
— рівняння вільного руху тіла, g — прискорення його вільного падіння. Знайти миттєву швидкість тіла в будь-який момент часу; у момент часу t = 2 c.
Ø За означенням маємо
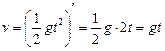 .
.
Зокрема, якщо t = 2, дістаємо:
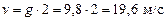 .▲
.▲
Сформулюємо тепер розглянуту задачу мовою геометрії.
Нехай дано функцію у = f(x), графік якої наведено на
рис. 2. Диференціальне відношення 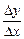 дорівнює тангенсу кута b, утвореного січною, що проходить через точки Р та Q, які мають відповідно абсциси х та х + Dх, із додатним напрямом вісі Ох.
дорівнює тангенсу кута b, утвореного січною, що проходить через точки Р та Q, які мають відповідно абсциси х та х + Dх, із додатним напрямом вісі Ох.
Якщо приріст Dх ® 0, то точка Q прямує до точки P, а кут b — до кута a, утвореного дотичною до розглядуваної кривої в даній точці з додатним напрямом осі Ох. Отже, маємо:
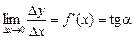 . (6)
. (6)
Значення похідної в деякій точці дорівнює тангенсу кута, утвореного дотичною до кривої в цій точці з додатним напрямом осі Ох.
Приклад. Знайти тангенси кутів нахилу дотичної до кривої
у = х2 у точках М1(½; ¼), М2(–1; 1) (рис. 3).

Рис. 3
Ø Згідно з (6) дістаємо:
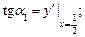
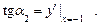
За формулою похідної степеневої функції маємо: 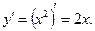
Отже,
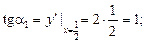
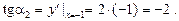
Рівняння дотичної
та нормалі до кривої
Розглянемо рівняння кривої у = f(x) (рис. 4). Візьмемо на кривій точку М(х1, у1) і запишемо рівняння дотичної до цієї кривої в точці М, припускаючи, що дотична не паралельна жодній координатній осі.
Рівняння кривої, що має кутовий коефіцієнт k і проходить через точку М, набирає вигляду
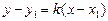 .
.
Для дотичної 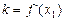 , тому рівняння дотичної буде таке:
, тому рівняння дотичної буде таке:
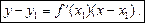
Поряд із дотичною до кривої розглядають і її нормаль.
Нормаллю до кривої в даній точці називається пряма, яка проходить через цю точку і перпендикулярна до дотичної в ній.
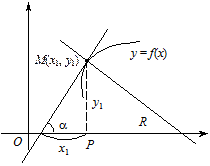
Рис. 4
Із означення нормалі випливає, що її кутовий коефіцієнт kнорм пов’язаний із кутовим коефіцієнтом k дотичної рівністю
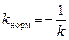 , тобто
, тобто
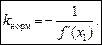
Отже, дістаємо рівняння нормалі до кривої у = f(x) у точці
М (х1, у1):
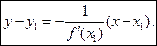
Приклад. Записати рівняння дотичної та нормалі до кривої
у = х3 у точці М(1; 1).
· Оскільки у¢ = 3х2, то кутовий коефіцієнт дотичної
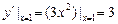 .
.
Отже, згідно з (1) рівняння дотичної буде таке:
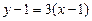 , або
, або 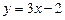 .
.
Рівняння нормалі:
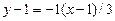 , або
, або 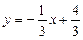 (рис. 5).
(рис. 5).

Рис. 5
1. Знайти похідну функції.
1) 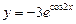 ; 2)
; 2) 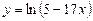 ;
;
3) 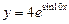 ; 4)
; 4) 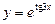 ;
;
5) 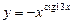 ; 6)
; 6) 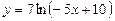 ;
;
7) 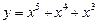 ; 8)
; 8) 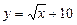 ;
;
9) 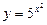 ; 10)
; 10) 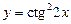 .
.
2. В якій точці похідна функції 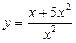 дорівнює 7?
дорівнює 7?
3. Скласти рівняння дотичної до графіка функції 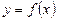 в точці
в точці 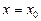 :
:
1) 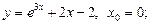
2) 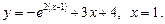
4. Знайти 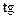 кута похилу графіка функції
кута похилу графіка функції 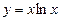 в точці
в точці 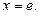
5. В яких точках графіка функції 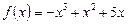 дотична до нього утворює тупий кут з віссю абсцис?
дотична до нього утворює тупий кут з віссю абсцис?
6. Знайти 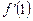 , якщо
, якщо 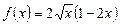 .
.
7. Знайти похідну функції.
1) 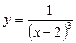 ; 2)
; 2) 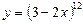 ;
;
3) 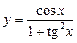 ; 4)
; 4) 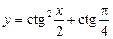 ;
;
5) 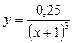 ; 6)
; 6) 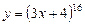 ;
;
7) 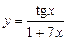 ; 8)
; 8) 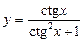 ;
;
9) 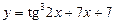 ; 10)
; 10) 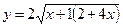 .
.
8. Знайти приріст функції 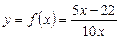 в точці
в точці 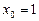 , якщо
, якщо 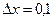 .
.
9. Вибрати функцію, для якої не існує похідної в точці 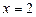 .
.
1) 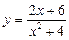 ; 2)
; 2) 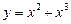 ;
;
3) 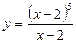 ; 4)
; 4) 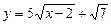 .
.
10. Розв’язати рівняння 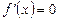 , якщо:
, якщо:
1) 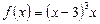 ; 2)
; 2) 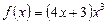 ;
;
3) 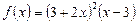 ; 4)
; 4) 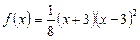 .
.
Дата добавления: 2019-11-25; просмотров: 192; Мы поможем в написании вашей работы! |

Мы поможем в написании ваших работ!
