Оценка параметров систем уравнений

7.1. Невзаимозависимые системы

, e - k-вектора-строки центрированных значений изучаемых (эндогеных) переменных и их случайных ошибок; E( e ) = 0, E( e ^/ e ) = s ² W;

 - n-вектор-строка центрированых значений независимых факторов (экзогенных переменных);

A - n ´ k-матрица коэффициентов регрессии;

 - система уравнений регрессии;

e - та же система по N наблюдениям; в каждом наблюдении матожидание ошибок равно нулю, их матрица ковариации одинакова (равна s ² W) и они не скоррелированы по наблюдениям.

                                    ,

где , т.е. факт скоррелированности ошибок разных изучаемых переменных ( ) не создает дополнительных проблем, и уравнения системы могут оцениваться по отдельности с помощью обычного МНК.

Пусть для коэффициентов матрицы A имеются априорные ограничения, и эта матрица имеет, например, следующую структуру:

                                  ,

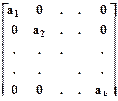где a_i - n_i-вектор-столбец коэффициентов в i-м уравнении (для i-й изучаемой переменной); . Т.е. для каждой изучаемой переменной имеется свой набор объясняющих факторов с N ´ n_i-матрицей наблюдений 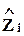 ( ), и система уравнений записывается как совокупность внешне не связанных между собой уравнений:

                      , .

Поскольку ошибки скоррелированы, правильная оценка параметров регрессии дается решением следущих уравнений:

          ,

где  - элемент матрицы W ^-1.

Эта оценка совпадает с обычной МНК-оценкой 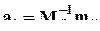, если матрица W диагональна.

 

7.2. Взаимозависимые или одновременные уравнения. Проблема идентификации.

 

Уравнения регрессии записываются в форме без свободного члена.

X - N ´ k-матрица наблюдений за изучаемыми переменными x;

Z - N ´ (n+1)-матрица наблюдений за независимыми факторами z;

B - k ´ k-матрица параметров регрессии при изучаемых переменных;  и b _ll = 1 - условия нормализации, т.е. предполагается, что в конечном счете в левой части l-го уравнения остается только l-я переменная, а остальные изучаемые переменные переносятся в правую часть;

A - (n+1) ´ k-матрица параметров регрессии при независимых факторах;

e - N ´ k-матрица значений случайных ошибок e по наблюдениям;

xB = zA + e, или XB = ZA + e - структурная форма системы уравнений регрессии;

x = zAB ^{- 1} + e B ^{- 1}, или X = ZAB ^{- 1} + e B ^{- 1} - приведенная форма системы;

D = AB ^{- 1} - (n+1) ´ k-матрица параметров регрессии приведенной формы. Для их оценки используется МНК: .

                        DB - A = 0 или WH = 0,

где (n+1) ´ (n+k+1)-матрица ,

(n+k+1) ´ k-матрица ,

- условия для оценки параметров структурной формы.

В общем случае этих условий недостаточно. Необходимы дополнительные условия. Пусть для параметров l-го уравнения имеется дополнительно r _l условий:

                                     R _lh _l = 0,

где R _l - r _l ´ (n+k+1)-матрица дополнительных условий;

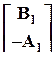 - (n+k+1)-вектор-столбец  параметров l-го уравнения - l-й столбец матрицы H.

 - общие условия для определения структурных параметов l-го уравнения, где W_l - (n+r _l+1) ´ (n+k+1)-матрица.

Они позволяют определить искомые параметры с точностью до постоянного множителя (с точностью до выполнения условий нормализации b _ll = 1), если ранг матрицы W_l равен n+k. Для этого необходимо, чтобы ; необходимо и достаточно, чтобы ранг матрицы R _lH равнялся k - 1.

l-е уравнение не идентифицировано, если ; оно точно идентифицировано, если  и ранг W_l равен n+k; сверхидентифицировано, если  и строки R_l линейно не зависмы.

Обычно строки матрицы R_l являются ортами, т.е. дополнительные ограничения исключают некоторые переменные из структурной формы. Тогда, если k_l и n _l - количества, соответственно, изучаемых переменных и независимых факторов в l-м уравнении, то для его идентификации необходимо, чтобы .

Дальнейшее изложение ведется в предположении, что строки матрицы R_l - орты.

 

7.3. Оценка параметров отдельного уравнения

X^l - N ´ k_l-матрица наблюдений за изучаемыми переменными x^l, входящими в l-е уравнение;

X_l - N-вектор-столбец наблюдений за l-й переменной x _l;

 - N ´ (k_l - 1)-матрица X^l без столбца X_l наблюдений за ;

b ^l - k_l-вектор-столбец параметров при изучаемых переменных в l-м уравнении;

b _l - (k_l - 1)-вектор-столбец b ^l с обратным знаком и без l-го элемента (без элемента b _ll = 1);

Z ^l - N ´ (n _l+1)-матрица наблюдений за независимыми факторами z^l, входящими в l-е уравнение;

a _l - (n _l+1)-вектор-столбец параметров при этих факторах;

e _l - N-вектор-столбец остатков e _l в l-м уравнении по наблюдениям;

 или  - l-е уравнение регрессии.

Применение обычного МНК к этому уравнению дает в общем случае смещенные оценки.

Если данное уравнение точно идентифицировано, то для оценки его параметров можно использовать косвенный метод (КМ) наименьших квадратов. С помощью МНК оцениваются параметры приведенной формы системы уравнений, через которые однозначно выражаются структурные параметры данного уравнения. Можно записать уравнения для этой оценки. Действительно, условия

                                   

эквивалентны

                           ,

где  - k_l ´ k-матрица, полученная из I_k вычеркиванием нужных строк;

 - аналогичная (n _l+1) ´ (n+1)-матрица для A_l.

Тогда для B_l и A_l, удовлетворяющим требуемым условиям, выполняется следующее:

                 ,

и требования WH_l = 0 можно записать в форме (переходя к обозначениям оценок соответствующих величин)

, (т.к.  и )

                                   или ,

где (n+1)-вектор-столбец  (l-й столбец матрицы D);

(n+1) ´ (k_l - 1)-матрица 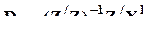 (матрица, составленная из столбцов матрицы D, соответствующих переменным ).

Это - система уравнений для нахождения искомых параметров. Она имеет единственное решение в случае точной идентификации уравнения, т.е., если ее матрица

                                              

квадратна, размерности n+1 и не вырождена (необходимое и достаточное условие точной идентификаци уравнения).

Для сверхидентифицированного уравнения можно применить двухшаговый метод (2М) наименьших квадратов.

На 1-м шаге с помощью МНК оцениваются параметры приведенной формы для переменных :

                                ,

где V^l - N ´ (k_l-1)-матрица остатков по уравнениям;

и определяются расчетные значения этих переменных (“очищенные” от ошибок):

                          .

На 2-м шаге с помощью МНК оцениваются искомые параметры структурной формы из уравнения:

                            .

Можно определить единый оператор 2М-оценивания. Поскольку

 и ,

этот оператор записывается так (1-я форма оператора):

, или в более “прозрачной” - 2-й форме (учитывая, что ):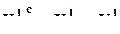

.

Если уравнение не идентифицировано, то обращаемая матрица в данном операторе вырождена. Если уравнение точно идентифицировано, то 2М-оценка совпадет с КМ-оценкой.

Для сверхидентифицированного уравнения можно использовать также метод наименьшего дисперсионного отношения (МНДО). Строгое обоснование его применимости вытекает из метода максимального правдоподобия.

Пусть b^l в уравнении X ^lb^l = Z ^la _l + e _l оценено, и X ^lb^l рассматривается как единая эндогенная переменная. В результате применения МНК определяются:

             ,

             ,

              .

Теперь находится остаточная сумма квадратов при условии, что все экзогенные переменные входят в l-е уравнение. Она равна

                    , где .

Тогда b^l должны были бы быть оценены так, чтобы

                 .

(иначе было бы трудно понять, почему в этом уравнении присутствуют не все экзогенные переменные).

Решение этой задачи приводит к следующим условиям:

                 ,

из которых f находится как минимальный корень соответствующего характеристического уравнения, а b^l определяется с точностью до постоянного множителя (с точностью до нормировки b_ll = 1).

В общем случае f > 1, но . Если данное уравнение точно идентифицировано, то f = 1, и МНДО-оценки совпадают с КМ- и 2М-оценками.

Оператор

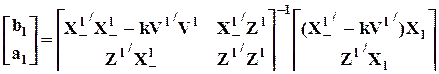
позволяет получить так называемые оценки k-класса (не путать с k - количеством эндогенных переменных в системе).

При k = 0, они являются обычными МНК-оценками для l-го уравнения; при k = 1, это - 2М-оценки; при k = f, - МНДО-оценки. 2М-оценки занимают промежуточное положение между МНК- и МНДО-оценками (т.к. f > 1). Исследования показывают, что эффективные оценки получаются при k < 1.

 

7.4. Оценка параметров всех (идентифицированных) уравнений

Из приведенной формы системы уравнений следует, что

          ,

и далее , т.е. в общем случае все эндогенные переменные скоррелированы с ошибками во всех уравнениях. Это является основным препятствием для применения обычного МНК ко всем уравнениям по отдельности.

Но в случае, если в матрице B все элементы, расположенные ниже главной диагонали, равны нулю (т.е. в правой части l-го уравнения могут появляться только более младшие эндогенные переменные , и последней компонентой любого вектора x^l является x_l), а в матрице W, наоборот, равны нулю все элементы, расположенные выше главной диагонали или эта матрица диагональна, то e _l не скоррелирован с переменными  при любом l. Это - рекурсивная система, и для оценки ее параметров можно применять МНК к отдельным уравнениям.

Для оценки параметров всех идентифицированных уравнений системы можно применить трехшаговый метод (3М) наименьших квадратов.

Предпологается, что идентифицированы все k уравнений:

              ,

где .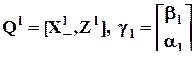

При условии, что матрица ковариации ошибок эндогенных переменых s ² W одинакова во всех наблюдениях (гипотеза гомоскедастичности)

        .

В уравнении                        (*)

 рассматривается как вектор n+1 наблюдений за одной эндогенной переменной, а  - как матрица n+1 наблюдений за n_l+k_l+1 экзогенными переменными. Поскольку матрица ковариации остатков по этому уравнению равна  (т.е. отлична от s ² I_N), для получения оценок c_l параметров g _l нужно использовать ОМНК:

        .

Это - еще одна (3-я) форма записи оператора 2М-оценивания.

Первые два шага 3М совпадают с 2М, но цель их не в получении оценок c_l, а в том, чтобы оценить e_l, и затем получить оценки W матрицы s ² W:

                               .

Теперь все уравнения (*) записываются в единой системе:

                 (**) ,

или

                                  ,

где Y - соответствующий k(n+1)-вектор-столбец наблюдений за изучаемой переменной;

Q - ´ -матрица наблюдений за экзогенными переменными;

g - - вектор-столбец параметров регрессии;

h - k(n+1)-вектор столбец остатков по наблюдениям.

Легко проверить, что матрица ковариации остатков h удовлетворяет следующему соотношению:

                                   ,

где Ä - операция прямого умножения матриц.

Для нее имеется оценка: k(n + 1) ´ k(n + 1)-матрица .

Эта матрица отлична от , поэтому на 3-м шаге 3М-оценивания к единой системе (**) применяется ОМНК и получается окончательная оценка c параметров g:

                        

В таком виде оператор 3М-оценивания используется для всех сверхидентифицированных уравнений. Для точно идентифицированных уравнений он имеет более сложную форму. Но для таких уравнений всегда можно применить КМ-оценивание.

 

---

Дата добавления: 2019-11-25; просмотров: 141; Мы поможем в написании вашей работы!

Поделиться с друзьями:

---

---

Мы поможем в написании ваших работ!