Обработка результатов эксперимента

Саратовский Государственный Технический Университет

Кафедра прикладной физики

Лист учета выполнения лабораторной работы

Теоретический отчет	Допуск	Измерения	Окончательный отчет

Общее количество лабораторных работ:

Выполнил студент

Яковлев Александр

Группы Б4-ЭЛЭТ 13

Семестр 2019-2020 уч. года

Лектор

Ассистент

Физический маятник

Цель работы: изучение гармонических колебаний, определение приведенной длины физического маятника и ускорения свободного падения.

Основные понятия

Простейшим типом колебаний является гармоническое колебание, когда смещение тела от положения равновесия зависит от времени по закону синуса или косинуса

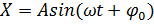или (1)

Основные характеристики колебаний- Амплитуда, частота, период.

Частота колебаний ровна числу полных колебаний, совершаемых за единицу времени, измеряется частота в Герц (Гц). Периодом колебаний называется промежуток времени, за которое совершается полное колебание. Период связан с частотой соотношением . Циклическая или круговая частота ровна количеству полных колебаний за время равное 2π секунд: 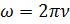. Тело совершает гармонические колебания, когда на него действует упругая сила, пропорциональная величине смещения от положения равновесия

(2)

Запишем для колебательного(колеблющегося) тела второй закон Ньютона:

или (3)

Перепишем уравнения и введем обозначения:

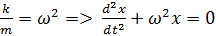(4), (5)

Это и есть дифференциальное уравнение гармонических колебаний

, – циклическая частота собственных колебаний, где

. (6)

При гармоничном колебании непрерывно меняется кинетическая энергия, так же и потенциальная. Кинетическая энергия колеблющейся точки m:

потенциальная энергия:

Полная энергия мат. точки, совершающая гармоническое колебание с частотой ω и амплитудой А:

Если сила сопротивления среды пропорциональна скорости колебания, то есть , второй закон Ньютона для колеблющейся точки записывается или (7)

Введем обозначения (8)

Амплитуда затухающих колебаний уменьшается по закону:

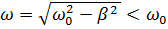(9)

Если , частота является мнимым числом и имеет место апериодический процесс

Рис.1

В случае затухающих колебаний энергия убывает по закону:

(10)

Величина отношения энергии к мощности потерь за время характеризуют способность колебательной системы сохранять энергию и называется добротностью:

. (11)

Степень затухания колебаний характеризуется логарифмическим декрементом, определяет затухания колебаний за период:

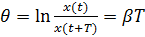(12)

Для изучения колебаний используется физический или математический маятник. Момент силы mg относительно оси 0 равен:

. При самых малых углах отклонения закон вращательного движения выглядит: или (13)

где J-момент инерции маятника относительно оси вращения.

(14)

описывает гармонические колебания. Период таких колебаний равен: (15), в случае малых углов отклонения дифференциальное уравнение выглядит: (16)

Период колебаний математического маятника (17)

Физический маятник описываемый (13), колеблется также как и маятник (16), 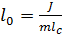Если к оси маятника подвесить грузик на нити такой длины, чтобы она была ровна приведенной длине данного маятника, то отклоненные на одинаковый угол маятник и грузик колеблются вместе. По теореме Штейнера момент инерции относительно оси маятника по этому приведенная длина будет , т.е. больше

Теорема Гюйгенса: если физический маятник подвесить за центр качания, его период не изменится, и прежняя точка подвеса будет новым центром качания. Расстояние от центра тяжести до новой оси , где - прежняя приведенная длина, - расстояние от центра тяжести до прежней оси. Поэтому новая приведенная длина будет равна: (18)

где - момент инерции маятника относительно оси .

По теореме Штейнера: , откуда

(19)

Где – момент относительно оси, проходящей через центр тяжести. Но с другой стороны , так как , подставив в (19), получим: (20)

Мы получили, что – обратимость точки подвеса и центра качаний.

Методика Эксперимента

Обратный маятник состоит из стального стержня, на котором закрепляются опоры 1 и 2 в виде призм и грузы 3 и 4.

Время N полных колебаний маятника измеряется секундомерами. В автоматическом режиме секундомер включается при срабатывании фото-электрического датчика 6, выключается кнопкой “стоп”.

Метод оборотного маятника основан на сопряженности двух его точек подвеса и центра качания. Путем изменения расстояний между опорами или между грузами добиваются такого расположения грузов на стержне, чтобы период колебаний маятника при его переворачивании не изменился. При выполнении этого условия расстояние между опорами будет являться приведенной длиной маятника .

Если расстояние от груза 4 до опоры 1 обозначить , то расстояние от центра масс (с) до опор выразится: 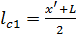, (21)

, (22)

Порядок Выполнения Работы

1. Закрепите груз 3 на некотором расстоянии от опоры ( должно находиться в пределах отрезка 4-12 см), измерьте время 10-15 колебаний и определите период колебаний маятника при положении груза .

2. Не изменяя точки опоры передвиньте груз в новое положение и определите . Определите периоды еще для 3-х положений груза.

3. Подвесьте маятник за другую опору. Определите периоды колебаний при тех же положениях груза, что и в п.п.1,2.

4. По результатам п.п.1-3 постройте графики зависимости периода колебаний от положения груза 3, найдите координаты точки их пересечения: .

5. Закрепите груз на расстоянии от опоры. Определите период колебаний и 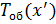, повторив измерения 3 раза. Рассчитайте среднее значение Т.

Измерьте расстояние между опорами и расстояние от опоры до груза 4.

Обработка результатов эксперимента

1.Используя результаты, полученные в п.5 предыдущего раздела и формулу (17), определить приведенную длину маятника: 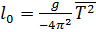сравнить эту величину с расстоянием между опорами .

2.Используя значения , по формулам (21) рассчитать положение центра масс физического маятника.

3.По формулам (22) рассчитать моменты инерции физического маятника относительно осей, проходящих через опоры 1 и 2.

4.По формуле найти ускорение свободного падения.

Расчет погрешности

1. Погрешность измерения приведенной длины физического маятника: ; ;

2. Погрешность измерения центра тяжести физического маятника:

3. Расчет погрешности момента инерции и относительно опор 1 и 2: и

4. Погрешность определителя g рассчитывается по формуле:

№	1	2	3	4	5
X1
T1
X2
T2
X3
T3
X4
T4
X5
T5












α

Дата добавления: 2019-11-16; просмотров: 137; Мы поможем в написании вашей работы!

Поделиться с друзьями:

Мы поможем в написании ваших работ!