Дифференциальное уравнение вращательного движения твердого тела вокруг неподвижной оси

Динамика

1) Осн.законы механики (зак-ны Галилея-Нютона): закон инерции (1-ый закон): материальная точка сохраняет состояние покоя или равномерного прямолинейного движения до тех пор, пока действие других тел не изменит это состояние; основной закон динамики ( 2-ой закон (Ньютона)): ускорение матер.точки пропорционально приложенной к ней силе и имеет одинаковое с ней направление 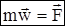; закон равенства действия и противодействия (3-й закон (Ньютона)): всякому действию соответствует равное и противоположно направленное противодействие; закон независимости сил: несколько одновременно действующих на матер.точку сил сообщают точке такое ускорение, какое сообщила бы ей одна сила, равная их геометрической сумме. Масса m - мера инертности тела. F=ma. Принцип суперпозиции

Пусть на материальную точку действует некоторая система сил и требуется определить движение точки под действием этих сил.

Уравнение второго закона динамики для материальной точки массой m запишется в виде

m⋅ a = ΣF_i(1)

где a - ускорение точки;

F_i- силы, действующие на точку, включая реакции связей.

Спроецировав уравнение (1) на декартовы оси координат, получим систему из трех уравнений

m⋅ a_x = ΣF_xi

m⋅ a_y = ΣF_yi(2)

m⋅ a_z = ΣF_zi

где a_x, a_y, a_z- проекции ускорения точки на декартовы оси координат;

F_xi, F_yi, F_zi - проекция i-той силы на соответствующую ось.

Учитывая, что

получаем систему дифференциальных уравнений первого порядка относительно проекций скорости точки

или второго порядка относительно координат точки

Спроецировав уравнение (1) на естественные оси координат, получим следующую систему уравнений

где a_τи a_n - касательное и нормальное ускорение точки;

F_τi, F_ni, F_bi - проекция i-той силы на касательную, нормаль и бинормаль соответственно.

Учитывая, что

a_τ= dV/dt, a_n = V²/ρ, a_b = 0

получим:

mdV/dt = ΣF_τi,

mV²/ρ = ΣF_ni, (5)

0 = ΣF_bi.

В зависимости от того, что известно о движении точки, дифференциальные уравнения записывают или в декартовых или в естественных координатах.

Две основные задачи динамики: первая задача динамики – зная закон движения точки, определить Первая, основная задача динамики точки заключается в том, чтобы по заданному закону движения материальной точки определить результирующую или одну из составляющих сил, действующих на эту точку.

При наличии нескольких сил, действующих на точку, второй закон Ньютона дает основное уравнение динамики точки

где m – масса точки;

a – ускорение точки;

F_i– силы, действующие на точку.

В зависимости от способа задания движения точки, это уравнение можно записать по-разному.

Вторая, основная задача динамики точки заключается в том, чтобы по заданным силам, действующим на точку, определить ее движение.

Уравнение второго основного закона динамики для материальной точки массой mзапишется в виде

где a – ускорение точки;

F_i – силы, действующие на точку, включая реакции связей.

Спроектировав уравнение (4.1) на декартовы оси координат, получим систему из трех уравнений

где a_x , a_y, a_z – проекции ускорения точки на декартовы оси координат;

F_x, F_y, F_z – проекция i -й силы на соответствующую ось.

4) Свободные и вынужденные колебания

Материальная точка М массой m движется прямолинейно под действием восстанавливающей силы F, направленной к центру колебания О.

F = -cx,

где c - постоянный коэффициент пропорциональности.

Дифференциальное уравнение колеблющейся материальной точки

c/m = k²

Получили линейное дифференциальное уравнение 2-го порядка с постоянными коэффициентами. Общее решение этого уравнения имеет вид

x = C₁coskt + C₂sinkt

Уравнение гармонических колебаний материальной точки, где C₁ и C₂ - прозвольные постоянные, определяемые по начальным условиям движения t = 0, x = x₀ , V = V₀;

V = dx/dt = -C₁ ksinkt + C₂ kcoskt

x₀= C₁, V₀ = C₂ k  C₁ = x₀ , C₂ = V₀ /k, подставим в (1.98), получим

искомый закон движения точки М.

Для анализа свободных колебаний дифференциальное уравнение лучше представить в амплитудной форме, где C₁=A sinα, C₂=A cosα

x = A sin(kt +α),

следовательно, в случае прямолинейного движения под действием притягивающей силы, пропорциональной расстоянию от центра притяжения, материальная точка совершает гармонические колебания.

Величина наибольшего отклонения точки М от центра О, называется амплитудой – A колебания; аргумент (kt + α) называется фазой колебания; α – начальная фаза колебания, k – круговая частота колебаний. График гармонических колебаний - синусоида.

Скорость точки определяется по формуле:

V = dx/dt = Аkcos(kt + α)

Амплитуда A и начальная фаза α определяются по начальным условиям движения. Пусть при t = 0, абсцисса точки М = x₀, а скорость V₀.

x₀ = Аsinα , V₀ =Аkcosα , получаем

А = и tgα =

Полный период колебаний -T

T = 2π /k или T = 2π

Частота и период свободных колебаний точки зависят лишь от массы этой точки и от коэффициента с, характеризующего восстанавливающую силу, и не зависят от начальных условий движения, k = 2 π /T - круговая частота колебаний определяет число полных колебаний, которые совершает точка в течение 2π секунд.

Затухающие колебания при действии R_x= – b сила сопротивления, пропорциональная скорости (вязкое трение). , обозначив b/m=2n, получаем:

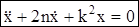, характеристическое уравнение: z² + 2nz + k²= 0, его корни:

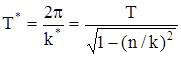z_1,2= . а) При n<k корни мнимыеÞ общее решение дифф.ур-ия имеет вид: , обозначив С₁=Аsinb, C₂=Acosb Þ x=Ae^-^ntsin(kt+b). Множитель e^-^nt показывает, что колебания затухающие. График заключен между двумя симметричными относительно оси t кривыми x=±Ae^-^nt. Из начальных условий: , ; частота затухающих колебаний: k^*= ; период: , период затухающих колебаний больше периода свободных колебаний (при небольших сопротивлениях Т^*»Т). Амплитуды колебаний уменьшаются: – декремент колебаний; –nT^*/2 логарифмический декремент; "n" – коэффициент затухания.

Б) Апериодическое движение точки при n ³ k или b ³ 2 . При n > k корни характеристич-ого ур-я вещественны, общее решение: , обозначая С₁=(В₁+В₂)/2, С₂=(В₁-В₂)/2, (ch, sh – гиперболические косинус и синус), если ввести В₁= Аshb, В₂= Аchb, то – это уравнение не колебательного движения (апериодического), т.к. гиперболический синус не является периодической функцией. При n = k корни характеристич. ур-я вещественны, равны и отрицательны: z₁=z₂= – n, общее решение: 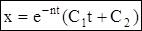, или , движение также апериодическое.

Вынужденные колебания кроме восстанавливающей силы действует переменная возмущающая сила, обычно, по гармоническому закону: Q = Hsin(pt+d), р – частота возмущающей силы, d – начальная фаза. , h=Н/m, – дифференциальное уравнение вынужденных колебаний (неоднородное линейное дифф-ное ур-ие). Его общее решение = сумме общего решения однородного уравнения и частного решения данного уравнения:

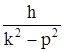х = х^*+х^**. х^*= C₁coskt + C₂sinkt, х^**= Asin(рt+d) – частное решение ищется в виде подобном правой части уравнения. Подставляя решение в уравнение, находим , х = C₁coskt + C₂sinkt+ sin(рt+d). Величина статического отклонения: А_ст= Н/с, – коэфф-нт динамичности, во сколько раз амплитуда колебаний превосходит статическое отклонение. При p=k m=¥ – явление резонанса (частота возмущающей силы равна частоте собственных колебаний, при этом амплитуда неограниченно возрастает). При p/k»1 наступает явление, называемое биениями: . Обозначая , получаем x=A(t)cos(pt+d) – происходит наложение дополнительных колебаний, вызванных возмущающей силой, на собственно вынужденные колебания – колебания частоты р, амплитуда которых является периодической функцией.

Явление резонанса возникает при совпадаении частот вынужденных и свободных кол-ний точки p=k. Дифур: 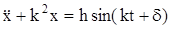. Частное решение:

х^**= Вtcos(kt+d), B=–h/(2k), т.е. общее решение дифура: х = C₁coskt + C₂sinkt – –h/(2k)tcos(kt+d). Ур-ние показывает, что амплитуда вынужденных колебаний при резонансе возрастает пропорционально времени. Период

Т=2p/k, фаза вынужденных колебаний отстает от фазы возмущающей силы на p/2.

Для получения дифференциальных уравнений движения материальной точки в неинерциальной системе отсчета воспользуемся теоремой сложного движения точки, рассматривая ее движение одновременно в двух системах координат – основной 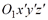(инерциальная система отсчета) и подвижной . Пусть 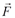 равнодействующая сил, действующих на точку M. В инерциальной системе отсчета: .

Воспользуемся выражением для абсолютного ускорения точки (теорема Кориолиса):

. Тогда , или .

Величины и имеют размерность силы. Вводя обозначения:

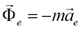 переносная сила инерции,

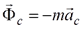 кориолисова сила инерции,

получаем основное уравнение динамики относительного движения

Уравнение движения в подвижной системе координат не совпадает с основным уравнением динамики, следовательно, соответствующая система отсчета не является инерциальной. Чтобы получить уравнение движения точки в неинерциальной системе отсчета, необходимо добавить переносную и кориолисову силы инерции.

Дифференциальные уравнения относительного движения материальной точки имеют вид:

7) Под механической системой в механике понимается совокупность материальных точек (тел), движения которых взаимосвязаны между собой.

Система материальных точек, движение которых не ограничено никакими связями, называется системой свободных материальных точек (примером являются планеты солнечной системы, движение которых по орбитам определяется действующими на них силами).

Определяющим признаком механической системы является наличие сил взаимодействия между отдельными материальными точками (телами) системы. Действие связей на точки (элементы) механической системы выражается силами, называемыми реакциями связей. Поэтому все силы, действующие на систему несвободных точек, можно разделить на две группы: задаваемые (активные) силы и реакции связей. В то же время все силы, действующие на точки любой механической системы (свободной или несвободной), можно подразделить и по другому признаку: на внешние и внутренние силы.

Внешними называются силы, действующие на точки (тела) системы со стороны материальных точек (тел), не входящих в состав данной механической системы.

Внутренними называются силы взаимодействия между материальными точками (телами) данной механической системы.

Одна и та же сила может быть как внешней, так и внутренней, в зависимости от того, какая механическая система рассматривается. Так, например, реакции подшипников вала являются внешними силами относительно вала. Эти же реакции относятся к внутренним силам, когда рассматривается вся установка.

Рассмотрим механическую систему, состоящую из k материальных точек (тел) M₁,M₂,M₃,...M_k c соответствующими массами m₁,m₂,m₃,...,m_k(рисунок 1.1).

Введем следующие определения:

m_j⊗ r_j- статический момент массы материальной точки относительно центра (полюса) О;

∑m_j⊗ r_j - статический момент массы механической системы относительно центра (полюса);

∑m_j= M - масса механической системы (арифметическая сумма масс точек системы).

Центром масс механической системы называется такая геометрическая точка C, сконцентрируя в которой (мысленно) массу M всей механической системы, получим, что ее статический момент массы равен статическому моменту массы всей механической системы, т.е.

M⊗ r_c= ∑m_j⊗ r_j (1.1)

Отсюда

Проецируя обе части равенства (1.2) на оси координат, получаем аналитические формулы для координат центра масс механической системы:

Выражению (1.2) можно придать и другой вид, если умножить числитель и знаменатель ее правой части на ускорение силы тяжести . В этом случае

где P_j= m_j⋅g ( j = 1,2,3,...,n ) – веса материальных точек, образующих механическую систему;

∑P_j = M⋅g = G – вес всей механической системы.

Выражение (1.4) определяет радиус-вектор центра тяжести неизменяемой материальной системы в предположении, что она находится в поле силы тяжести. Отсюда следует, что центр тяжести неизменяемой (жесткой) механической системы (в частности твердого тела) совпадает с центром масс.

Однако понятия о центре масс и центре тяжести механической системы не являются тождественными. Понятие о центре тяжести как о точке, через которую проходит линия действия равнодействующей сил тяжести, по существу имеет смысл только для твердого тела, находящегося в однородном поле тяжести.

Понятие же о центре масс как о характеристике распределения масс в механической системе является более широким, так как имеет смысл для любой механической системы независимо от того, находится ли данная система под действием каких-либо сил или нет. Поэтому понятие центра тяжести можно рассматривать как частный случай по отношению к понятию центра масс.

В общем случае следует говорить о центре масс материальной (механической) системы, а не о центре тяжести. При определении центра масс материальной системы можно пользоваться методами, установленными в статике для определения центра тяжести (метод симметрии, метод расчленения на простейшие элементы, метод отрицательных масс и т.д.).

8) Момент инерции тела относительно оси. Радиус инерции.

В механике вводится еще одна характеристика распределения масс - момент инерции. Моментом инерции тела (системы) относительно данной оси Oz (или осевым моментом инерции) называется скалярная величина, равная сумме произведений масс всех точек тела (системы) на квадраты их расстояний от этой оси

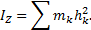. При непрерывном распределении масс (тело) сумма переходит в интеграл: J_x= ò(y²+z²)dm; J_y= ò(z²+x²)dm; J_z= ò(x²+y²)dm – относительно координатных осей. J_z= M×r², r – радиус инерции тела – расстояние от оси до точки в которой нужно сосредоточить всего тела, чтобы ее момент инерции равнялся моменту инерции тела. Момент инерции относительно оси (осевой момент инерции) всегда >0. Полярный момент инерции J_o= ò( x²+y²+z²)dm; J_x+J_y+J_z= 2J_o

Момент инерции имеет размерность [кг∙м²]

Из определения: момент инерции тела (или системы) относительно любой оси является величиной положительной и не равной нулю.

Заметим также, что момент инерции тела – это геометрическая характеристика тела, не зависящая от его движения.

Осевой момент инерции играет при вращательном движении тела такую же роль, какую масса при поступательном, т.е. что осевой момент инерции является мерой инертности тела при вращательном движении и зависит от распределения массы тела относительно оси вращения.

Согласно формуле момент инерции тела равен сумме моментов инерции всех его частей относительно той же оси. Для одной материальной точки, находящейся на расстоянии h от оси, .

Часто в ходе расчетов пользуются понятием радиуса инерции. Радиусом инерции тела относительно оси Оz называется линейная величина 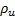, определяемая равенством

где М - масса тела. Из определения следует, что радиус инерции геометрически равен расстоянию от оси Оz той точки, в которой надо сосредоточить массу всего тела, чтобы момент инерции одной этой точки был равен моменту инерции всего тела.

Моменты инерции некоторых однородных тел:

стержень массы m и длины L: ; .

Однородный сплошной диск с центром в точке С радиуса R и массы m: . Полый цилиндр: ,

цилиндр с массой распределенной по ободу (обруч): .

Теорема Гюйгенса-Штейнера:

Момент инерции тела относительно данной оси равен моменту инерции относительно оси, ей параллельной, проходящей через центр масс тела, сложенному с произведением массы всего тела на квадрат расстояния между осями.

9)Теорема о движении центра масс системы.

Произведение массы системы на ускорение ее центра масс равно геометрической сумме всех действующих на систему внешних сил 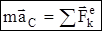– дифференциальное уравнение движения центра масс. В проекциях на оси координат: .

Закон сохранения движения центра масс. Если главный вектор (векторная сумма) внешних сил остается все время равным нулю, то центр масс механической системы находится в покое или движется прямолинейно и равномерно. Аналогично в проекциях на оси, если Þ , если при этом в начальный момент v_Cx₀= 0, то Þ Þ x_C= const.

10) Количество движения системы Q (иногда обозначают К) – вектор, равный геометрической сумме (главному вектору) количеств движения всех точек системы:

, М – масса всей системы, v_C – скорость центра масс.

Теорема об изменении количества движения системы: – производная по времени от количества движения механической системы геометрически равна главному вектору внешних сил, действующих на эту систему. В проекциях: , и т.д. Теорема об изменении кол-ва движения системы в интегральной форме:

, где – импульсы внешних сил.

В проекциях: Q₁_x – Q₀_x = åS^e_kx и т.д. количество движения системы за некоторый промежуток времени равно сумме импульсов действующих на систему внешних сил за тот же промежуток времени. Закон сохранения количества движения – если сумма всех внешних сил, действующих на систему, = 0, то вектор количества движения системы будет постоянен по модулю и направлению: Þ = const, аналогично в проекциях: Þ Q_x= const. Из закона следует, что внутренние силы изменить суммарное количество движение системы не могут. Тело переменной массы , масса которого непрерывно изменяется с течением времени m= f(t) (пр.: ракета, топливо которой убывает). Дифф-ное уравнение движения точки переменной массы:

– уравнение Мещерского, u – относительная скорость отделяющихся частиц. – реактивная сила, — секундный расход топлива, . Реактивная сила направлена в противоположную сторону относительной скорости истечения топлива.

Формула Циолковского: — определяет скорость ракеты, когда все топливо будет израсходовано – скорость в конце активного участка, m_т– масса топлива, m_k– масса корпуса ракеты, v₀ – начальная скорость. – число Циолковского, m₀ – стартовая масса ракеты. От режима работы ракетного двигателя, т.е. от того насколько быстро сжигается топливо, скорость ракеты в конце периода горения не зависит. Для достижения 1-ой космической скорости 7,9 км/с, при m₀/m_k= 4, скорость отброса должна быть 6 км/с, что трудно осуществить, поэтому применяются составные (многоступенчатые) ракеты.

11) Главный момент количеств движения матер. системы (кинетический момент) – величина, равная геометрической сумме моментов количеств движения всех точек системы относительно центра О. . Теорема об изменении момента количеств движения системы (теорема об изменении кинетического момента):

— производная по времени от кинетического момента механич. системы относительно некоторого неподвижного центра геометрически равна главному моменту внешних сил, действующих на эту систему относительно того же центра. Аналогичные равенства относительно осей координат: и т.д.

Закон сохранения кинетического момента: если , то . Главный момент количеств движения системы является характеристикой вращательного движения. Кинетический момент вращающегося тела относительно оси вращения равен произведению момента инерции тела относительно этой оси на угловую скорость тела: K_z = J_zw. Если M_z= 0, то J_zw = const, J_z – момент инерции тела.

12) Кинетический момент вращающегося тела

Пусть тело вращается вокруг неподвижной оси Z.

Определим К_Z

Возьмем точку К на расстоянии h_К от оси. Она будет иметь скорость, равную

V_К =w h_К, где w - угловая скорость тела.

Тогда .

Для всего тела . Величину называют моментом инерции тела относительно оси вращения Z, тогда: .Кинетический момент вращающегося тела относительно оси вращения равен произведению момента инерции тела относительно этой оси на угловую скорость тела.

Если система состоит из нескольких тел, вращающихся вокруг одной оси, то

Дифференциальное уравнение вращательного движения твердого тела вокруг неподвижной оси

Для изучения вращательного движения твердого тела вокруг неподвижной оси воспользуемся теоремой об изменении момента количества движения (кинетического момента) механической системы относительно оси (3.10):

dK_z/dt = M_z^e. (3.11)

Пусть на твердое тело, имеющее неподвижную ось вращения z (рисунок 3.4), действует система заданных внешних активных сил (F₁, F₂, F₃,...,F_n ), определяющих угловую скорость ω и угловое ускорение ε этого тела в его вращательном движении вокруг оси z. Одновременно на это же тело действуют силы реакции R_A подпятника иR_B радиального подшипника.

Определяем правую часть уравнения (3.11):

M_z^e= ∑M_z(F_j^e) + M_z(R_A) + M_z(R_B).

Поскольку M_z(R_A) = M_z(R_B) = 0, то M_вращ = M_z^e= ∑M_z(F_j^e).

Найдем момент количества движения (кинетический момент) K_z вращающегося твердого тела. Для этого выделим точку M_j тела на расстоянии r_j от оси вращения и имеющую скорость V_j = ω⋅r_j. Очевидно, что K_zj = m_j ⋅ V_j⋅ r_j= m_j ⋅ω ⋅r_j². Тогда момент количества движения (кинетический момент) всего вращающегося тела будет:

K_z = ∑K_zj = ∑m_j ⋅ω ⋅r_j²,

где ∑m_j⋅r_j²= J_z.

Следовательно, окончательно будем иметь

K_z = J_z⋅ ω.

получаем J_z⋅ dω/dt = M_вращ, или J_z⋅d²φ/dt²= M_вращ. (3.13)

Уравнение (3.13) представляет собой дифференциальное уравнение вращательного движения твердого тела вокруг неподвижной оси.

Поскольку dω/dt = ε, имеем ε = M_вращ/J_z. (3.14)

Полученное выражение (3.14) показывает, что осевой момент инерции J_z тела следует рассматривать как меру инертности твердого тела при его вращательном движении вокруг неподвижной оси.

13) Работа силы. Мощность. Элементарная работа dA = F_tds, F_t – проекция силы на касательную к траектории, направленная в сторону перемещения, или dA = Fdscosa.

Если a – острый, то dA>0, тупой – <0, a=90^o: dA=0. dA= – скалярное произведение вектора силы на вектор элементарного перемещения точки ее приложения; dA= F_xdx+F_ydy+F_zdz – аналитическое выражение элементарной работы силы. Работа силы на любом конечном перемещении М₀М₁: . Если сила постоянна, то = F×s×cosa. Единицы работы:[1 Дж (джоуль) = 1 Нм].

, т.к. dx= dt и т.д., то .

Теорема о работе силы: Работа равнодействующей силы равна алгебраической сумме работ составляющих сил на том же перемещении А=А₁+А₂+…+А_n.

Работа силы тяжести: 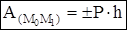, >0, если начальная точка выше конечной.

Работа силы упругости: 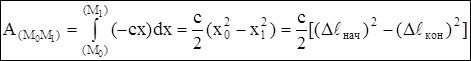–работа силы упругости равна половине произведения коэффициента жесткости на разность квадратов начального и конечного удлинений (или сжатий) пружины.

Работа силы трения: если сила трения const, то - всегда отрицательна, F_тр=fN, f – коэфф.трения, N – нормальная реакция поверхности.

Работа силы тяготения. Сила притяжения (тяготения): , из mg= , находим коэфф. k=gR². – не зависит от траектории.

Мощность – величина, определяющая работу в единицу времени, . Если изменение работы происходит равномерно, то мощность постоянна: N=A/t. [1 Вт (ватт) =1 Дж/с, 1 кВт (киловатт) =

= 1000 Вт].

14-15)

16-17) Возможная (виртуальная) работа dА – элементарная работа, которую, действующая на матер.точку сила могла бы совершить на возможном перемещении этой точки.

Связи являются идеальными, если сумма элементарных работ реакций этих связей при любом возможном перемещении системы равна нулю, т.е. SdА^r=0.

Принцип возможных перемещений: для равновесия механической системы с идеальными связями необходимо и достаточно, чтобы сумма элементарных работ всех действующих на нее активных сил при любом возможном перемещении была равна нулю. 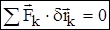или в проекциях: .

Принцип возможных перемещений дает в общей форме условия равновесия для любой механической системы, дает общий метод решения задач статики.

Если система имеет несколько степеней свободы, то уравнение принципа возможных перемещений составляют для каждого из независимого перемещений в отдельности, т.е. будет столько уравнений, сколько система имеет степеней свободы.

Общее уравнение динамики – при движении системы с идеальными связями в каждый данный момент времен сумма элементарных работ всех приложенных активных сил и всех сил инерции на любом возможном перемещении системы будет равна нулю. Уравнение использует принцип возможных перемещений и принцип Даламбера и позволяет составить дифференциальные уравнения движения любой механической системы. Дает общий метод решения задач динамики. Последовательность составления: а) к каждому телу прикладывают действующие на него задаваемые силы, а также условно прикладывают силы и моменты пар сил инерции; б) сообщают системе возможные перемещения; в) составляют уравнения принципа возможных перемещений, считая систему находящейся в равновесии.

17) Принцип Даламбера (метод кинетостатики)

В каждый момент движения сумма активных сил, реакций связей и сил инерции равна нулю — принцип Даламбера для материальной точки.

– внешняя сила, – внутренняя сила. Сила инерции: , знак (–) показывает, что сила инерции направлена в противоположную сторону ускорению.

Для системы добавляется уравнение моментов: .

Обозначают: 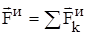– главный вектор сил инерции, 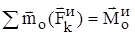– главный момент сил инерции. Учитывая, что геометрическая сумма внутренних сил и сумма их моментов равна нулю , , получаем: , — уравнения кинетостатики. принцип Даламбера для системы: если в любой момент времени к каждой из точек системы, кроме фактически действующих на ней внешних и внутренних сил, приложить соответствующие силы инерции, то полученная система сил будет находиться в равновесии и к ней можно будет применять все уравнения статики.

Главный вектор и главный момент сил инерции твёрдого тела.

Система сил инерции твёрдого тела можно заменить одной силой, равной и приложенной в центре О, и парой с моментом, равным . Главный вектор системы сил, как известно, не зависит от центра приведения и может быть вычислен заранее. Т.к. , то

Следовательно, главный вектор сил инерции тела, совершающего любое движение, равен произведению массы тела на ускорение его центра масс и направлен противоположно этому ускорению.

Прикладывается главный вектор к точке приведения, которую можно назначить в любом месте, т.е. он не зависит от выбора этой точки.

Если ускорение 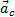разложить на касательное и нормальное, то вектор разложиться на составляющие

С определением главного момента сил инерции возникает немало сложностей. Рассмотрим несколько частных случаев.

1. Поступательное движение. В этом случае тело никакого вращения вокруг центра масс С не имеет. Отсюда заключаем, что , и равенство (1) даёт .

Следовательно, при поступательном движении силы инерции твёрдого тела приводят к одной равнодействующей, равной и проходящей через центр масс тела.

2. Плоскопараллельное движение. Пусть тело имеет плоскость симметрии и движется параллельно ей. Вследствие симметрии главный вектор и результирующая пара сил инерции, так же как и центр масс С тела, лежат в плоскости симметрии.

Тогда, помещая центр приведения в точке С, получим из равенства (16) 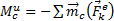. С другой стороны . Отсюда заключаем, что

Таким образом, в рассмотренном случае движение системы сил инерции приводится к результирующей силе, равной [формула (18)] и приложенной в центре масс С тела (рис.7), и к лежащей в плоскости симметрии тела паре, момент которой определяется формулой (18). Знак минус в формуле показывает, что направление момента противоположно направлению углового ускорения тела.

3. Вращение вокруг оси, проходящей через центр масс тела. Пусть опять тело имеет плоскость симметрии, а ось вращения СZ перпендикулярна к этой плоскости и проходит через центр масс тела. Тогда данный случай будет частным случаем предыдущего. Но при этом а следовательно, и .

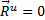Таким образом, в рассмотренном случае система сил инерции приводится к данной паре, лежащей в плоскости, перпендикулярной к оси вращения тела, и имеющей момент

19) Общее уравнение динамики – при движении системы с идеальными связями в каждый данный момент времен сумма элементарных работ всех приложенных активных сил и всех сил инерции на любом возможном перемещении системы будет равна нулю. Уравнение использует принцип возможных перемещений и принцип Даламбера и позволяет составить дифференциальные уравнения движения любой механической системы. Дает общий метод решения задач динамики. Последовательность составления: а) к каждому телу прикладывают действующие на него задаваемые силы, а также условно прикладывают силы и моменты пар сил инерции; б) сообщают системе возможные перемещения; в) составляют уравнения принципа возможных перемещений, считая систему находящейся в равновесии

Возможная (виртуальная) работа dА – элементарная работа, которую, действующая на матер.точку сила могла бы совершить на возможном перемещении этой точки.

Дата добавления: 2019-09-13; просмотров: 577; Мы поможем в написании вашей работы!

Поделиться с друзьями:

Мы поможем в написании ваших работ!