Формулировка критерия Михайлова:

⇐ ПредыдущаяСтр 2 из 2

Автоматическая система управления, описываемая уравнением п-го порядка, устойчива, если при изменении ω от 0 до ∞ характеристический вектор системы D (jω) повернется против часовой стрелки на угол nπ/2, не обращаясь при этом в нуль.

Это означает, что характеристическая кривая устойчивой системы должна при изменении с ω до 0 до ∞ пройти последовательно через n квадрантов. Из приведенных выше выражений следует, что кривая D (jω) всегда начинается в точке на действительной оси, удаленной от начала координат на величину а_п.

Характеристические кривые, соответствующие устойчивым системам (рис. б), имеют плавную спиралеобразную форму и уходят в бесконечность в том квадранте, номер которого равен порядку уравнения. Если характеристическая кривая проходит п квадрантов не последовательно или проходит меньшее число квадрантов, система неустойчива (рис. в).

Если кривая D (jω) проходит через начало координат, то система находится на границе устойчивости. Действительно, если характеристическое уравнение имеет один нулевой корень р _k = 0 (апериодическая граница устойчивости) или одну пару чисто мнимых корней р _k = ± jβ_k (колебательная граница устойчивости), то функция D (jω) при ω = 0 или ω = β_k обратится в нуль.

В практических расчетах удобно применять следствие из критерия Михайлова:

Система устойчива, если действительная и мнимая части характеристической функции D ( j w ) обращаются в нуль поочередно (см. рис. г)), т.е. если корни уравнений Re ( w )=0 и Im ( w )=0 перемежаются и Re (0) > 0 и Im ¢ (0) > 0.

Следствие из критерия Михайлова позволяет установить устойчивость системы невысокого порядка аналитически, без построения годографа.

17. Критерий Найквиста

Критерий Найквиста был сформулирован в 1932 г. американским физиком X. Найквистом. В отличие от критериев Гурвица, Рауса и Михайлова, которые основаны на анализе характеристического уравнения системы, критерий Найквиста позволяет судить об устойчивости замкнутой системы по амплитудно-фазовой характеристике разомкнутого контура системы.

В этом заключается существенное преимущество критерия, т.к. построение АФХ разомкнутого контура для большинства реальных систем оказывается проще, чем построение годографа Михайлова. Особенно упрощается это построение для одноконтурных систем, состоящих из типовых звеньев.

Основная формулировка критерия Найквиста:

Автоматическая система управления устойчива, если амплитудно-фазовая характеристика W ( jω ) разомкнутого контура не охватывает точку с координатами (–1; j0).

Эта формулировка справедлива для систем, которые в разомкнутом состоянии устойчивы. Таковыми являются большинство реальных систем, состоящих из устойчивых элементов.

На рисункеизображены амплитудно-фазовые характеристики разомкнутого контура, соответствующие трем различным случаям: система устойчива (кривая 1); система находится на колебательной границе устойчивости (кривая 2); система неустойчива (кривая 3).

Для использования изложенного приема применительно к астатическим системам, которые содержат интегрирующее звено, и амплитудно-фазовые характеристики которых начинаются в бесконечно удаленной точке, характеристику W (jω) предварительно дополняют дугой окружности бесконечно большого радиуса на угол πr/2, где r – степень астатизма системы (см. рис.)

Для суждения об устойчивости систем, имеющих АФХ сложной конфигурации, когда кривая АФХ пересекает действительную ось левее точки (–1; j0) несколько раз, можно также использовать правило переходов, сформулированное советским ученым Я. 3. Цыпкиным: АФХ не охватывает точку (–1; j0), т. е. система устойчива, если при возрастании ω разность между числом положительных (сверху вниз) и отрицательных (снизу вверх) переходов АФХ через ось абсцисс слева от точки (-1; j0) равна нулю.

Если АФХ начинается или заканчивается на отрезке (- ∞;-1), то считают, что характеристика совершает полперехода.

Частота, при которой амплитудная характеристика А (ω) [модуль функции W (jω)] принимает значение 1, называется частотой среза и обозначается ω_ср. Частоту, при которой фазовый сдвиг φ (ω) = - π, обозначают ω_π.

Пользуясь введенными обозначениями, можно записать условие нахождения системы на границе устойчивости:

ω_ср = ω_π

Частота, с которой система колеблется на границе устойчивости, называется критической и обозначается ω_кр.

Таким образом, особая роль точки (-1; j0) заключается в том, что она, во-первых, соответствует превращению отрицательной обратной связи в положительную, и во-вторых, является граничной между режимами усиления и ослабления сигналов звеном W (jω).

Иногда на практике встречаются системы, в контуре которых имеется одно или несколько неустойчивых элементов. Такие системы в разомкнутом состоянии неустойчивы.

Для суждения об их устойчивости в замкнутом состоянии используют (обобщенную) формулировку критерия Найквиста:

Автоматическая система управления устойчива, если амплитудно-фазовая характеристика W (jω) разомкнутого контура охватывает l /2 раз точку с координатами (-1; j0), где l – число правых корней характеристического уравнения разомкнутого контура.

Количество охватов при этом можно определять по правилу Цыпкина как разность между числом положительных и отрицательных переходов.

Из обеих формулировок следует, что для суждения об устойчивости системы необходимо предварительно установить устойчивость ее в разомкнутом состоянии (и число правых корней характеристического полинома). Обычно эта вспомогательная задача решается сравнительно легко, при помощи критерия Рауса: для этого приравнивают к нулю знаменатель передаточной функции W(р) разомкнутого контура и анализируют данное характеристическое уравнение.

Во многих практических случаях устойчивость разомкнутого контура может быть оценена без каких-либо вычислений непосредственно по виду входящих в контур звеньев.

Устойчивость системы управления и запас устойчивости могут быть определены также с использованием пары характеристик: АЧХ и ФЧХ.

Примеры

1. т = 2

2. т = 2

Система неустойчива.

3. т=5

Устойчива.

18. Запас устойчивости

Чтобы система была работоспособна, она должна быть устойчивой. Но просто устойчивости еще может оказаться недостаточно, и тому есть две причины. Во-первых, устойчивая система кроме всех остальных качеств должна иметь приемлемые временные характеристики. Кроме того, модель, используемая при анализе и синтезе системы управления, никогда не является точной. Следовательно, работа с моделью может показать, что система устойчива, тогда как реальная система окажется неустойчивой. Поэтому обычно требуют, чтобы система не просто была устойчивой, но и обладала некоторым запасом устойчивости.

По этим двум причинам вводится понятие относительной устойчивости системы. Будем характеризовать относительную устойчивость степенью близости диаграммы Найквиста к точке –1. Это проиллюстрировано на рис. а. Заметим, что вектор, проведенный из точки –1 к диаграмме Найквиста, соответствует выражению , где есть передаточная функция разомкнутой системы. Минимальное значение амплитуды этого вектора является хорошим показателем относительной устойчивости замкнутой системы, однако на практике этот показатель используется достаточно редко. Вместо этого обычно используются два показателя, приведенные на рис. б.

Первый из этих показателей — это запас устойчивости по амплитуде. Запас по амплитуде определяется как число, на которое должен быть умножен коэффициент усиления разомкнутой системы, чтобы замкнутая система оказалась на границе устойчивости. На рис. б координата точки пересечения диаграммой Найквиста отрицательного направления действительной оси обозначена как 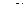. Если передаточную функцию разомкнутой системы умножить на коэффициент , то диаграмма Найквиста пройдет через точку –1, и замкнутая система окажется на границе устойчивости. Поэтому можно дать следующее определение:

Запас устойчивости по амплитуде. Если диаграмма Найквиста для разомкнутой системы пересекает отрицательное направление действительной оси в точке 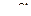и при этом замкнутая система устойчива, то запас по амплитуде равен . Если диаграмма Найквиста имеет несколько пересечений отрицательного направления действительной оси, то запас по амплитуде определяется по той точке, которая дает наименьшее значение .

Вторым часто используемым показателем относительной устойчивости является запас по фазе:

Запас устойчивости по фазе. Запас по фазе определяется наименьшей величиной угла, на который надо повернуть диаграмму Найквиста, чтобы она прошла через точку -1.

На рис. б запас по фазе обозначен как угол . Он определяется на той частоте, при которой амплитуда функции равна единице. Тогда запас по фазе

Теперь определим третий показатель относительной устойчивости. Этот показатель, используемый в современной теории управления, представляет собой знаменатель передаточной функции замкнутой системы, , и называется возвратной разностью.

Минимум возвратной разности – это наименьшее значение , , где 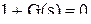есть характеристическое уравнение системы.

Если возвратная разность минимальна на частоте, при которой имеет вещественное значение, то она непосредственно указывает на запас по амплитуде. Если же она минимальна на частоте, при которой , то это определяет запас устойчивости по фазе. Из рис. а видно, что минимум возвратной разности — это минимальное расстояние от диаграммы Найквиста до точки –1. Увеличивая это расстояние, мы повышаем устойчивость системы. При анализе и синтезе систем методами классической теории управления минимум возвратной разности используется редко.

19. Качество переходного процесса

19.1 Оценка качества по переходной характеристике

Оценку запаса устойчивости и быстродействия можно произвести по виду кривой переходного процесса в системе автоматического регулирования при некотором типовом входном воздействии, которым может быть как задающее, так и возмущающее воздействие. В качестве типового входного воздействия рассматривается обычно единичный скачок. В этом случае кривая переходного процесса для регулируемой величины будет представлять собой переходную характеристику системы.

Она может строиться для регулируемой величины или для ошибки .

Склонность системы к колебаниям, а, следовательно, и запас устойчивости могут быть охарактеризованы максимальным значением регулируемой величины или так называемым перерегулированием (выражается в %)

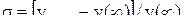
где представляет собой установившееся значение регулируемой величины после завершения переходного процесса

Допустимое значение перерегулирования для той или иной системы автоматического регулирования может быть установлено на основании опыта эксплуатации подобных систем. В большинстве случаев считается, что запас устойчивости является достаточным, если величина перерегулирования не превышает 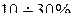. Однако в некоторых случаях требуется, чтобы переходный процесс протекал вообще без перерегулирования, т. е. был монотонным; в ряде других случаев может допускаться перерегулирование .

Быстродействие системы может определяться по длительности переходного процесса 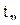. Длительность переходного процесса определяется как время, протекающее от момента приложения на вход единичного скачка до момента, после которого имеет место неравенство

где — заданная малая постоянная величина, представляющая собой обычно допустимую ошибку. Величина 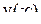в частном случае может равняться нулю.

Допустимое значение времени переходного процесса определяется на основании опыта эксплуатации систем регулирования. В следящих системах в качестве единичного скачка принимается мгновенное изменение управляющего воздействия . В этом случае под величиной обычно понимают некоторую долю входного воздействия, составляющую, как правило, от 1 до 5% величины скачка на входе.

Иногда дополнительно к величине перерегулирования σ (или к величине ) задается допустимое число колебаний, которое может наблюдаться в течение времени переходного процесса. Это число составляет обычно . В некоторых системах колебания могут вообще не допускаться, а иногда может допускаться до колебаний.

Графически требования к запасу устойчивости и быстродействию сводятся к тому, чтобы отклонение регулируемой величины не выходило при единичном входном воздействии из некоторой области, изображенной на рисунке.

Эта область называется областью допустимых отклонений регулируемой величины в переходном процессе.

В следящих системах удобно применять сформулированные требования качества к ошибке системы . В этом случае можно рассматривать область допустимых значений ошибки и при более сложных входных воздействиях, например при мгновенном приложении на входе постоянной скорости.

Дальнейшее развитие критериев качества, использующих переходную характеристику, приводит к введению дополнительных оценок качества (кроме введенных выше , и σ). К ним относятся следующие оценки:

1.Время запаздывания , равное отрезку времени, заключенному между моментом приложения входного скачкообразного сигнала и моментом времени, при котором осредненная выходная величина становится равной половине ее установившегося значения. Примененный здесь термин «осредненная» означает, чnо в случаях, когда на передний фронт выходного сигнала накладываются высокочастотные колебания (это может иметь место в системах высокого порядка), величина определяется по сглаженной кривой, аппроксимирующей реальную переходную характеристику системы.

2. Время нарастания , равное отрезку времени, заключенному между точкой пересечения оси времени с касательной, проведенной к осредненной кривой переходной характеристики в точке , и координатой t точки пересечения указанной касательной с горизонтальной прямой, соответствующей установившемуся значению регулируемой величины. Максимальное время нарастания 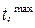ограничивается требуемым быстродействием. Минимальное время нарастания 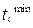ограничивается допустимыми в системе ускорениями и колебательными режимами.

Уточненная диаграмма качества переходного процесса изображена на рисунке.

19.2 Оценка качества по частотной характеристике

Построение кривой переходного процесса является в большинстве случаев весьма трудоемкой операцией. Поэтому целесообразно использовать методы, позволяющие определить вид переходной характеристики без построения всей кривой процесса. Это можно сделать по вещественной частотной характеристике замкнутой системы, которая используется для построения переходной функции. При этом предполагается, что переходный процесс вызван скачком задающего воздействия . Возможна оценка вида переходного процесса при приложении скачка возмущения . В этом случае необходимо использовать вещественную часть частотной передаточной функции системы по возмущающему воздействию

Использование оценки вида переходного процесса по вещественной частотной характеристике наиболее удобно применять в том случае, когда для исследования автоматической системы используются частотные методы.

Пусть вещественная частотная характеристика замкнутой системы имеет следующий вид (см. рис.)

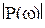Интервал частот , в котором , называется интервалом положительности. Интервал частот называется интервалом существенных частот. Если при и далее при величина становится и остается меньше некоторой заданной достаточно малой положительной величины 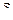, влиянием остальной части вещественной частотной характеристики (при ) на качество переходного процесса можно пренебречь. Если же при оказывается, что , то при оценке качества переходного процесса в первом приближении можно принимать во внимание только интервал положительности .

Заметим, что отбрасываемый «хвост» вещественной частотной характеристики ( или ) влияет главным образом на начальную часть переходного процесса, которая, следовательно, будет оцениваться более грубо. Начало же вещественной частотной характеристики определяет главным образом концевую часть переходного процесса.

На основании анализа интеграла были получены следующие оценки качества переходного процесса.

1. Статическое отклонение регулируемой величины, получающееся в результате единичного скачка внешнего воздействия, равно начальному значению вещественной частотной характеристики . Если речь идет о скачке задающего воздействия, то должно равняться либо 1,. либо некоторому 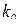,если система должна воспроизводить задающее воздействие в определенном масштабе 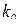. Если же вводится скачок возмущающего воздействия 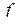то значение должно быть как можно меньше, причем в астатической системе возможно

2. Чтобы величина перерегулирования (кривая 1 на рис. а)не превышала 18% от статического отклонения, достаточно иметь положительную невозрастающую непрерывную характеристику - (кривая 1 на рис. б).

3. Для монотонности переходного процесса (кривая 2 на рис. а) достаточно, чтобы представляла собой отрицательную, убывающую по модулю непрерывную функцию от (кривая 2 на рис. б), причем .

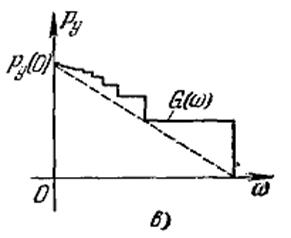
4. Простейшим признаком немонотонности переходного процесса является наличие значений (кривая 3 на рис. б). Переходный процесс тоже будет немонотонным, когда кривая располагается при каких-нибудь выше ступенчатой кривой G (со) (рис. в), причем

где через обозначены целочисленные значения, взятые с избытком; например, если , то берется .

5. В случае, если вещественная частотная характеристика имеет очертание вида кривой 3 (рис. б), которую можно представить как разность двух положительных невозрастающих непрерывных функций, то величина перерегулирования (рис. а) будет меньше, чем .

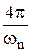6. Для монотонных процессов время затухания до значения от статического отклонения будет больше, чем . В общем же случае . При прочих равных условиях переходный процесс тем быстрее затухает, чем больше , т.е. чем больше растянута область положительности вещественной частотной характеристики вдоль оси .

7. Если заданную вещественную частотную характеристику можно приближенно заменить трапецией (рис. а), то в зависимости от отношения длин оснований и трапеции величина перерегулирования в процентах и время затухания переходного процесса в относительном виде могут быть приближенно оценены графиками, показанными на рис. б и в,причем величина заключается в интервале .

8. Если заданную характеристику можно приближенно заменить ломаной, изображенной на рис. а, причем то зависимость максимально возможного перерегулирования (в процентах) от величины отношения определяется кривой на рис. б.При этом заданной верхней границе допустимого значения времени затухания переходного процесса соответствует нижняя допустимая граница величины интервала положительности , определяемая кривой на рис.в.

9. Склонность системы к колебаниям тем больше, чем выше пик у вещественной характеристики. В частности, этот пик уходит в бесконечность, если система находится на границе колебательной устойчивости, что соответствует наличию пары чисто мнимых корней (кривая 1 на рисунке). При нахождении системы на границе устойчивости, соответствующей наличию одного нулевого корня, в бесконечность уходит начальное значение ординаты вещественной частотной характеристики (кривая 2).

На основании вышеуказанных простых признаков можно грубо оценивать качество переходного процесса в замкнутой автоматической системе по виду ее вещественных частотных характеристик и .

Для иллюстрации, приведем ряд кривых переходного процесса (рис. б), которые соответствуют вещественным частотным характеристикам замкнутой системы изображенным на рис. а.

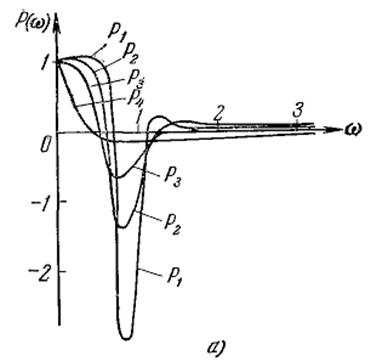
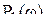Наилучший переходный процесс соответствует характеристике , а наихудший — характеристике , обладающей наибольшими пиками.

19.3 Корневые критерии качества переходного процесса

Вид корней характеристического уравнения определяет характер переходных процессов в системе автоматического регулирования. Поэтому можно сформулировать требования по запасу устойчивости и быстродействию системы, не рассматривая самих переходных процессов, а накладывая определенные условия на корни характеристического уравнения.

Передаточная функция любой системы может быть представлена в следующем виде:

где g _i – это нули передаточной функции; l _i – полюса передаточной функции (корни характеристического уравнения). l _i определяет устойчивость системы и качество переходных процессов, g _i определяет только качество переходных процессов.

В корневых методах используют так называемые корневые показатели, определяемые по расположению корней р₁, р₂, …, р_п характеристического уравнения замкнутой системы на комплексной плоскости.

1) Наиболее общим корневым показателем качества является среднее геометрическое значение модулей корней

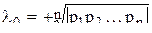которое легко вычисляется через крайние коэффициенты характеристического уравнения

. (*)

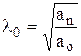l ₀ определяет центр расположения всех корней характеристического уравнения и влияет на быстродействие системы. Чем меньше показатель l ₀, тем ближе «созвездие» корней к мнимой оси и тем больше длительность переходного процесса.

В числитель подкоренного выражения (*) входит коэффициент , который зависит от передаточного коэффициента разомкнутого контура:

Отсюда можно сделать вывод: чем выше коэффициент усиления k, тем лучше быстродействие системы (при прочих равных условиях – одинаковой конфигурации “созвездия” корней).

Основное влияние на характер переходного процесса оказывают корни, расположенные ближе к мнимой оси, которые дают наиболее длительные составляющие переходного процесса и называются доминирующими.

2) Расстояние от мнимой оси до действительной части ближайшего к ней корня называется степенью устойчивости h.

3) Колебательные свойства системы регулирования предопределяет k–ая пара комплексных корней , для которой наибольшее отношение

или наибольший угол j между действительной осью и лучами, соединяющими начало координат с этими корнями. В данном случае такой парой являются комплексные корни р₂ и р₃.

Отношение m _д мнимой части b к действительной части a доминирующей пары комплексных корней называют степенью колебательности.

В практических расчетах чаще используют корневой показатель колебательности.

также определяемый через доминирующую пару комплексных корней. При выборе настроек регуляторов стремятся получить значения .

19.4 Интегральные критерии качества переходного процесса

Интегральные оценки имеют целью дать общую оценку быстроты затухания и величины отклонения регулируемой величины в совокупности, без определения того и другого в отдельности. Простейшей интегральной оценкой может служить величина

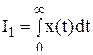
где — отклонение регулируемой величины от нового установившегося значения, которое она будет иметь после завершения переходного процесса.

В устойчивой системе при и этот интеграл имеет конечную величину. Геометрически это будет площадь под кривой переходного процесса, построенного для отклонения (рис. а).

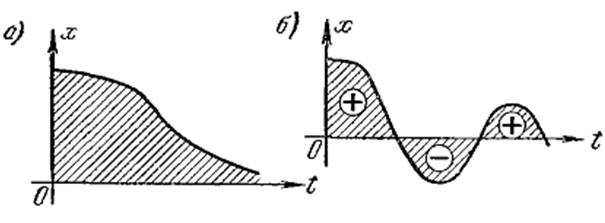
Площадь будет тем меньше, чем быстрее затухает переходный процесс и чем меньше величина отклонения. Поэтому параметры системы рекомендуется выбирать таким образом, чтобы добиваться минимума этой интегральной оценки.

Для вычисления интеграла I₁ нет необходимости в нахождении так как его можно легко вычислить, используя изображение Лапласа. Действительно, изображение Лапласа определяется выражением

Отсюда следует, что интеграл I₁ может быть найден посредством предельного перехода

Неудобством интегральной оценки вида I₁ является то, что она годится только для монотонных процессов, когда не меняется знак отклонения х. Если же имеет место колебательный процесс (рис. б), то при вычислении интеграла I₁ площади будут складываться алгебраически и минимум этого интеграла может соответствовать колебаниям с малым затуханием или вообще без затухания. Так как форма переходного процесса при расчете систем регулирования может быть неизвестна, то применять интегральную оценку вида I₁ оказывается практически нецелесообразным. Поэтому предлагалась другая интегральная оценка:

т. е. сумма абсолютных величин всех площадей по кривой переходного процесса. Но оказалось, что вычисление ее по коэффициентам уравнения затруднительно.

Квадратичная интегральная оценка. В свете вышесказанного целесообразно перейти к квадратичной интегральной оценке, называемой иногда «квадратичной площадью» регулирования:

(x → 0 при t → ∞)

которая не зависит от знаков отклонений, а значит, и от формы переходного процесса (монотонной или колебательной).

Величина I будет тем меньше, чем меньше сумма заштрихованных на рисунке площадей (взятых для квадратов ординат), т.е. чем лучше переходный процесс приближается к идеальному скачку регулируемой величины вслед за скачком задающего или возмущающего воздействия.

Недостатком интегральных оценок является то, что здесь ничем не ограничивается форма кривой переходного процесса. Оказывается, например, что три совершенно различных по форме процесса, изображенных на рисунке, имеют одно и то же значение квадратичной интегральной оценки I. Часто оказывается, что выбранные по минимуму этой оценки параметры системы соответствуют слишком сильно колебательному процессу, ибо отмечавшееся уже при этом стремление приблизить процесс к идеальному скачку вызывает большую скорость процесса при подходе к установившемуся значению .

Это получается вследствие того, что оценка I учитывает только величину отклонения и быстроту затухания и никак не учитывает близость системы к колебательной границе устойчивости.

Если, например, подать на вход системы единичный скачок, то ошибка в переходном процессе определится заштрихованной частью на рис. а. Очевидно, что величина интегральной оценки I будет тем меньше, чем ближе будет кривая переходного процесса к ломаной линии АОBС. Но приближение процесса к этой линии требует увеличения угла наклона кривой в начальной стадии процесса (приближение части кривой OD к отрезку ОB).

Увеличение же начальной скорости может вызвать значительное перерегулирование и, следовательно, малый запас устойчивости.

Поэтому применяется еще другой вид интегральной оценки, в которой ограничение накладывается не только на величину отклонения х, но также и на скорость отклонения х. Эта улучшенная квадратичная интегральная оценка имеет вид

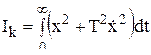
где T – некоторая постоянная времени.

Следует отметить, что абсолютное значение любой интегральной оценки само по себе не представляет интереса. Они служат лишь для сопоставления различных вариантов настройки одной и той же системы.

Удобство интегральных оценок состоит в том, что они дают единый числовой критерий качества. Недостатком является то, что одному и тому же значению интегральной оценки могут отвечать разные формы переходного процесса, что создает недостаточную определенность решения задачи.

20. Точность САУ

20.1 Коэффициенты ошибок

Назначение любой САУ – изменение выходной величины в соответствии с изменениями задающего воздействия. В большинстве случаев эта задача системы заключается в поддержании равенства при любых изменениях задающего и возмущающего воздействий.

При анализе точности различают две функции системы: воспроизведение задающего воздействия и подавление (компенсацию) возмущений.

Из-за инерционности объекта и регулятора обе эти функции выполняются любой реальной системой с погрешностью: в каждый момент времени после внешнего воздействия существует разность, характеризующая точность системы:

Если функция времени имеет произвольную форму, но достаточно плавную вдали от начальной точки процесса в том смысле, что через некоторое время существенное значение имеет только конечное число т производных

то ошибку системы можно определить следующим образом. Изображение ошибки

где — передаточная функция замкнутой системы по ошибке, — изображение задающего воздействия.

Разложим передаточную функцию по ошибке в ряд по возрастающим степеням комплексной величины р

сходящийся при малых значениях р, т.е. при достаточно больших значениях времени t, что соответствует установившемуся процессу изменения регулируемой величины при заданной форме управляющего воздействия. Переходя к оригиналу, получаем формулу для установившейся ошибки

Так как передаточная функция по ошибке представляет собой дробно-рациональную функцию, то коэффициенты ошибок можно более просто получить делением числителя на знаменатель.

Статическими называются такие САУ, у которых при постоянном задающем воздействии ошибка в установившемся режиме стремится к некоторой постоянной, неравной нулю. В таких системах коэффициент отличен от нуля.

Если регулятор или объект содержат интегрирующие звенья, то ошибка в установившемся режиме будет равна нулю, следовательно, система является астатической.

В системах с астатизмом первого порядка , а в системах с астатизмом второго порядка (2 интегрирующих звена) и .

При исследовании ошибки от возмущающего воздействия можно получить все коэффициенты не равными нулю при астатизме любого порядка, так как астатизму по задающему воздействию может соответствовать наличие статической ошибки по возмущению.

Если задающее воздействие имеет ограниченное число производных, то ряд будет иметь ограниченное число членов. Предположение, что коэффициенты ошибок представляют собой постоянные числа, обусловливает применение этого метода для сравнительно медленно меняющихся входных воздействий или когда можно пренебречь влиянием переходной составляющей процесса и рассматривать только вынужденное движение системы.

20.2 Методы повышения точности

К числу общих методов повышения точности систем автоматического управления относятся:

1) увеличение коэффициента усиления разомкнутой цепи;

2) повышение степени астатизма (введение интегрирующих и изодромных устройств);

3) применение регулирования по производным от ошибки.

Увеличение общего коэффициента усиления разомкнутой цепи является наиболее универсальным и эффективным методом. Увеличить общий коэффициент усиления можно обычно за счет введения в систему регулирования усилителей. Однако в некоторых случаях удается достичь этого увеличения за счет повышения коэффициентов передачи отдельных звеньев, например чувствительных элементов, редукторов и т. д.

Увеличение общего коэффициента усиления благоприятно сказывается в смысле уменьшения ошибок практически во всех типовых режимах. Это вытекает, в частности, из того, что общий коэффициент усиления разомкнутой цепи входит в качестве делителя во все коэффициенты ошибок

Однако увеличение общего коэффициента усиления ограничивается устойчивостью системы регулирования. При повышении коэффициента усиления, как правило, система приближается к колебательной границе устойчивости. При некотором предельном его значении в системе возникают незатухающие колебания. В этом сказывается противоречие между требованиями к точности и требованиями к устойчивости системы регулирования.

В связи с этим повышение общего коэффициента усиления до значения, при котором обеспечивается выполнение требований к точности, обычно может производиться только при одновременном повышении запаса устойчивости системы, что осуществляется при помощи так называемых корректирующих средств.

Повышение порядка астатизма. Повышение порядка астатизма используется для устранения установившихся ошибок в различных типовых режимах: в неподвижном положении, при движении с постоянной скоростью, при движении с постоянным ускорением и т. д. Формально это сводится к тому, чтобы сделать равными нулю первые коэффициенты ошибки системы. Физически повышение порядка астатизма осуществляется за счет введения в канал регулирования интегрирующих звеньев.

Передаточная функция интегрирующего звена

где — коэффициент передачи интегрирующего звена. представляет собой передаточную функцию разомкнутой системы регулирования до введения интегрирующего звена.

Результирующая передаточная функция разомкнутой системы будет иметь дополнительный множитель р в знаменателе:

Повышение порядка астатизма неблагоприятно сказывается на устойчивости системы. Поэтому одновременно с повышением порядка астатизма в системе автоматического регулирования приходится использовать корректирующие звенья, повышающие запас устойчивости

Применение изодромных устройств. Существует путь повышения порядка астатизма системы регулирования без заметного или недопустимого ухудшения ее запаса устойчивости. Этот путь заключается в применении изодромных устройств.

Передаточная функция изодромного устройства может быть представлена в виде

где — постоянная времени изодромного устройства.

Для дальнейшего повышения порядка астатизма системы регулирования могут применяться не один, а два, три и т. д. изодромных устройства. В этом случае можно получить повышение порядка астатизма на один, два, три и т. д. в зависимости от необходимости. Если исходная система имеет, например, астатизм первого порядка, то система с тремя изодромными устройствами будет обладать астатизмом четвертого порядка. В этом случае для коэффициентов ошибок будет иметь место равенство При соответствующем выборе постоянных времени изодромных устройств можно сохранить практически те же условия устойчивости, что и в исходной системе.

Регулирование по производным от ошибки. В большинстве случаев регулирование по производным от ошибки имеет целью повысить запас устойчивости системы, что позволяет увеличить общий коэффициент усиления системы и тем самым улучшить точность регулирования. Однако регулирование по производным от ошибки может самостоятельно повышать точность системы регулирования даже в том случае, когда сохраняется неизменным общий коэффициент усиления в системе. Физика этого явления заключается в том, что при введении регулирования по производным система начинает чувствовать не только наличие ошибки, но и тенденцию к изменению ее величины. В результате система регулирования более быстро реагирует на появление задающих и возмущающих воздействий, что снижает ошибку регулирования.

Передаточная функция части прямого канала вместе с включенным дифференцирующим элементом может быть представлена приближенно (в предположении, что дифференцирующий элемент является идеальным) в виде

где — постоянная времени дифференцирующей цепи.

В отличие от случая введения изодромного устройства, когда обращается в нуль первый, ранее отличный от нуля коэффициент ошибки, введение дифференцирующего элемента не влияет на этот коэффициент ошибки, но зато уменьшает последующие коэффициенты. В связи с этим наиболее эффективное снижение ошибки системы регулирования может быть достигнуто при одновременном использовании изодромных устройств и дифференцирующих элементов. Так как дифференцирование эквивалентно дополнительному усилению верхних частот, то использование более чем двух дифференцирующих элементов оказывается затруднительным вследствие возрастания влияния высокочастотных помех. Число же изодромных устройств ограничивается только получающимся усложнением системы регулирования. Однако и оно обычно не превышает трех.

21. Регуляторы. Законы регулирования

Под регулятором или управляющим устройством понимают преобразующее устройство, формирующее на основе ошибки управляющее воздействие, а объектом регулирования (управления) — собственно объект управления, объединенный с остальной (инерционной) частью управляющего устройства.

В промышленных регуляторах находят применение следующие типовые законы управления (в скобках указаны названия соответствующих регуляторов):

1. Пропорциональный закон или П-закон (пропорциональный регулятор или П-регулятор)

2. Пропоционально-интегральный закон или ПИ-закон (пропорционально-интегральный регулятор или ПИ-регулятор)

3. Пропорционально-дифференциальный закон или ПД-закон (пропорционально-дифференциальный регулятор или ПД-регулятор)

4. Пропоционалъно-интегро-дифференциалъный закон или ПИД-закон (пропорционалъно-интегро-дифференциальный регулятор или ПИД-регулятор)

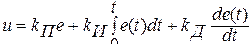
Здесь 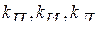— константы (передаточные коэффициенты).

Для выбора того или иного закона управления необходимо знать, какое влияние оказывает каждое из слагаемых, входящее в закон управления, на устойчивость и качество системы управления. Для выяснения этого вопроса рассмотрим работу системы управления при типовых законах управления, когда передаточная функция объекта имеет вид

П-закон. При П-законе передаточная функция регулятора и передаточная функция разомкнутой системы имеет вид

Характеристическое уравнение

имеет корни

Отсюда видно, что если объект управления является колебательным звеном , то замкнутая система при любом является также колебательным звеном, и степень колебательности с ростом возрастает.

Когда объект является апериодическим звеном 2-го порядка ( ), замкнутая система также является апериодическим звеном 2-го порядка при и колебательным звеном при .

Передаточные функции ошибки по задающему воздействию и по возмущению имеют вид

и для коэффициентов позиционной ошибки имеем

Отсюда видно, что при П-регуляторе рассматриваемая система является статической, и статическая ошибка убывает с ростом .

Однако начиная с с ростом увеличивается степень колебательности.

Таким образом, можно сделать вывод: с увеличением качество системы в установившемся режиме улучшается, а в переходном режиме ухудшается.

ПИ-закон. В этом случае передаточная функция разомкнутой системы имеет вид

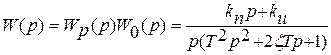
и характеристическое уравнение имеет вид

Коэффициенты этого уравнения положительны, определитель Гурвица 2-го порядка

при больше нуля и система устойчива, а при меньше или равен нулю и система неустойчива. Следовательно, увеличение коэффициента при интегральном члене приводит к неустойчивости системы. Естественно ожидать, что с увеличением в области устойчивости запасы устойчивости убывают, а степень колебательности увеличивается.

Так как передаточные функции ошибки имеют вид

то коэффициенты ошибок имеют вид

Таким образом, при включении интегрального слагаемого в закон управления система становится астатической, и с увеличением уменьшается скоростная ошибка. Однако при этом ухудшается качество системы в переходном режиме, и с определенного система становится неустойчивой.

ПД-закон. При этом законе , а передаточная функция разомкнутой системы

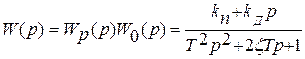
и характеристическое уравнение имеет вид

Корнями этого уравнения являются

Когда подкоренное выражение неотрицательно, т.е.

или

(34.1)

система управления является апериодическим звеном 2-го порядка.

Если выполняется противоположное неравенство, т.е.

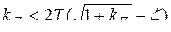(34.2)

то система является колебательным звеном, а степень устойчивости и степень колебательности соответственно принимают вид

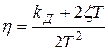
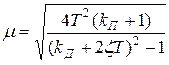
Следовательно, при выполнении условия (34.2) с ростом степень устойчивости возрастает, а степень колебательности убывает.

При выполнении условия (34.1) степень устойчивости имеет вид

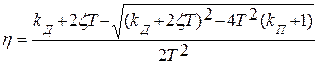
и, продифференцировав это выражение по , получим

Следовательно, в этом случае степень устойчивости с ростом убывает.

Передаточные функции ошибки имеют вид

и для коэффициентов позиционной ошибки имеем

Таким образом, введение в закон управления дифференцирующего члена улучшает качество системы в переходном режиме. На качество системы в установившемся режиме (при постоянных внешних воздействиях) он никакого влияния не оказывает. Но следует иметь в виду, что при чрезмерном увеличении качество системы в переходном режиме может ухудшиться.

ПИД-закон. В этом случае передаточная функция разомкнутой системы имеет вид

и характеристическое уравнение имеет вид

Определитель Гурвица 2-го порядка

выбором всегда можно сделать положительным.

Таким образом, введение в закон управления интегрирующего члена может сделать устойчивую систему неустойчивой, а введение дифференцирующего члена может сделать неустойчивую систему устойчивой.

Для коэффициентов ошибки имеем

Все основные выводы о влиянии дифференцирующего и интегрирующего членов на качество системы, полученные на основе рассмотрения ПИ-закона и ПД-закона управления, сохранятся и при рассмотрении ПИД-закона.

Итак, основные выводы таковы:

1) введение в закон управления интегрирующего члена делает систему астатической и улучшает качество системы в установившемся режиме, но оказывает дестабилизирующее влияние (т. е. может сделать систему неустойчивой) и ухудшает качество системы в переходном режиме;

2) введение в закон управления дифференцирующего члена оказывает стабилизирующее влияние (может сделать неустойчивую систему устойчивой) и улучшает качество системы в переходном режиме, не оказывая влияния на качество системы в установившемся режиме.

Хотя эти выводы получены на основе исследования системы с объектом 2-го порядка, есть основания считать, что они в основном справедливы и в более общем случае.

СПИСОК ИСПОЛЬЗОВАННОЙ ЛИТЕРАТУРЫ

1. Бесекерский В.А. Теория систем автоматического управления. / В.А. Бесекерский, Е.П. Попов – СПб: Изд-во «Профессия», 2007. – 752 с.

2. Кузьмин А.В. Теория систем автоматического управления: учебник / А.В. Кузьмин, А.Г. Схиртладзе. - Старый Оскол : ТНТ, 2009. - 224 с.

3. Первозванский А.А. Курс теории автоматического управления: учебное пособие. - 2-е изд., стер. - СПб. : Лань, 2010. - 624 с.

4. Коновалов Б.И. Теория автоматического управления: учебное пособие / Б.И. Коновалов, Ю.М. Лебедев. - 3-е изд., доп. и перераб. - СПб. : Лань, 2010. - 224 с.

5. Рапопорт Э.Я. Оптимальное управление системами с распределенными параметрами. – М., Высшая школа, 2009.

Учебное издание

Халапян Сергей Юрьевич

ОСНОВЫ ТЕОРИИ УПРАВЛЕНИЯ

Учебное пособие

(курс лекций)

Редактор: Иванова Н.И.

Компьютерный набор: Халапян С.Ю.

Корректор: Иванова Н.И.