Огнесохранность железобетонных конструкций

12.1 Если при проектировании здания ставится задача обеспечения сохранности несущих железобетонных конструкций после пожара, то предел их огнестойкости является недостаточным показателем. В этом случае на стадии проектирования следует обеспечить огнесохранность железобетонных конструкций.

При проектировании железобетонных конструкций, указанных в п. 4.21, должна быть проверена их огнесохранность после пожара длительностью, эквивалентной нормируемому пределу огнестойкости конструкции. При этом следует расчетно-аналитическим путем предусмотреть всевозможные последствия разрушающего воздействия пожара на наружные слои бетона и арматуру.

Огнесохранность железобетонной конструкции после пожара оценивается следующими характеристиками:

- необратимым (остаточным) прогибом (не более 1/150 пролета);

- необратимой потерей жесткости (не более 20%);

- необратимой потерей прочности (не более 10%).

Остаточная прочность после пожара

12.2 Расчеты остаточной прочности железобетонных элементов после пожара для нормальных и наклонных сечений производятся согласно указаниям раздела 8.

При применении упрощенного метода расчета - сопротивление сжатию бетона, нагретого выше критической температуры (см. п. 4.18), допускается не учитывать. Сопротивление бетона сжатию принимается равномерно распределенным по сжатой зоне. Расчетные сопротивления сжатию принимают равными R_b, расчетные сопротивления арматуры растяжению и сжатию после огневого воздействия при пожаре принимают соответственно равными R_st и R_sct.

Значение коэффициентов условий работы арматуры γ_st в охлажденном состоянии после пожара принимают по табл. 5.5 в зависимости от температуры нагрева арматуры во время пожара. Прогрев бетона до критической температуры во время пожара устанавливают по рис. 5.1, 8.1 и 8.2 и теплотехническим расчетом (см. приложения А, Б).

12.3 При расчете огнесохранности железобетонных конструкций по деформационной модели и с применением ЭВМ изменения свойств бетона после пожара учитывают по всему сечению элемента.

12.4 При расчете прочности нормальных сечений железобетонных элементов следует учитывать, что элементы, рассчитанные на работу до пожара при х ≤ ξ_R h₀, после пожара могут работать при х > ξ_R h_{0 t} из-за уменьшения сжатой зоны бетона после прогрева наружных слоев бетона выше критической температуры.

Когда условие х ≤ ξ_R h₀ не соблюдается, момент определяют по формулам (8.9) и (8.11), подставляя в них значения высоты сжатой зоны, определяемой по формуле

x = ξR h0

(12.1)

Значение ξ_R вычисляется по формуле

_{0588S10-01164}

ξ R = x / h0 = 0,8 / (1 + ε s,el / ε b,ult )

(12.2)

Относительная деформация растянутой арматуры при напряжениях, равных R _st, определяется

εs,el = Rst / Es

(12.3)

Относительную деформацию сжатого бетона ε_b,ult при напряжениях R_btem принимают равной ε_b2 по табл. 5.4.

12.5 При расчете на остаточную прочность после пожара усилия и деформации в нормальном к продольной оси элемента сечении на основе деформационной модели определяют согласно указаниям п.п. 8.25 - 8.27, используя диаграммы состояния бетона и арматуры, по расчетным сопротивлениям, со значениями коэффициентов условий работы γ_bt и γ_st в охлажденном состоянии после пожара. Модуль деформации бетона Е_b,τ определяют по формуле (5.4).

Расчет остаточного прогиба после пожара

12.6 Во время пожара в изгибаемых, внецентренно сжатых и внецентренно растянутых элементах при эксплуатационной нагрузке от огневого воздействия происходит развитие дополнительного прогиба из-за значительного нагрева растянутой арматуры и перепада температур по высоте сечения.

При температурах нагрева арматуры до 350°С прогиб железобетонного элемента развивается, в основном, за счет температурного расширения арматуры и бетона у более нагреваемой поверхности.

При более высоких температурах огневого воздействия прогиб развивается, в основном, из-за высокотемпературной ползучести арматуры.

При пожаре прогиб элемента возникает вследствие воздействия нагрузки и температуры.

После пожара в охлажденном состоянии прогиб от неравномерного нагрева по высоте сечения элемента уменьшается, и оставшаяся часть прогиба от нагрузки значительно больше, чем прогиб от нагрузки до пожара из-за снижения модуля упругости бетона и развития необратимых пластических деформаций арматуры при нагреве.

При остывании после пожара прочностные и упругопластические свойства бетона практически не восстанавливаются, а в арматуре происходит частичное восстановление прочности и полное восстановление упругости.

12.7  После пожара железобетонные элементы имеют трещины с нагреваемой стороны по всей длине пролета.

Для изгибаемых элементов, имеющих постоянную высоту по длине элемента, в пределах которой изгибаемый момент не меняет знак, кривизну допускается вычислять для наиболее напряженного сечения, принимая ее для остальных сечений изменяющейся пропорционально значению изгибаемого момента.

Для свободно опертых и консольных элементов максимальный прогиб допускается определять по формуле

f = s l² (1/r)_max, (12.4)

где s - коэффициент, зависящий от вида нагрузки и расчетной схемы элемента.          При действии равномерно распределенной нагрузки: для свободно опертой балки             s = 5/48, для консольной балки s = 1/4.

12.8 Кривизну изгибаемых, внецентренно сжатых и внецентренно растянутых элементов с трещинами в растянутой зоне определяют по формуле

(1/r)_max = (1/r)₁ - (1/r)₂ + (l/r)₃ - (l/r)_cs, (12.5)

где (l/r)₁ - кривизна от непродолжительного действия всей нагрузки, на которую производят расчет по деформациям;

(1/r)₂ - кривизна от непродолжительного действия постоянных и временных длительных нагрузок;

(1/r)₃ - кривизна от продолжительного действия постоянных и временных длительных нагрузок;

(1/r)_cs - кривизна от температурной усадки бетона.

12.9  Кривизна железобетонных элементов от действия нагрузки

(1/r) = M / D, (12.6)

где М - изгибаемый момент от внешней нагрузки (с учетом момента от продольной силы N) относительно оси нормальной плоскости действия изгибаемого момента и проходящей через центр тяжести приведенного поперечного сечения элемента;

D - жесткость приведенного поперечного сечения элемента, определяемая по формуле

D = E_b1 J_red (12.7)

12.10 Жесткость железобетонного элемента D без трещин в растянутой зоне определяют по формуле (12.7), в которой значение модуля деформации бетона принимают равным при непродолжительном действии нагрузки

E_b1 = 0,85E_bt, (12.8)

где Е_bt определяют по формуле (5.3), в которой коэффициент β_b принимают по табл. 5.1 в зависимости от температуры бетона в центре тяжести приведенного сечения.

При продолжительном действии нагрузок в формуле (12.8) Е_bt заменяют на Е_bτ, который определяют по формуле (5.4), принимая коэффициент φ_b,cr по табл. 5.1 в зависимости от температуры бетона в центре тяжести приведенного сечения.

12.11 Момент инерции приведенного поперечного сечения элемента относительно его центра тяжести определяют как для сплошного тела по общим правилам сопротивления упругих элементов, с учетом всей площади сечения бетона и площадей сечения арматуры с коэффициентом приведения арматуры к бетону

J_red = J + J_s α + J'_s α. (12.9)

Допускается определять момент инерции J _red без учета арматуры. Момент инерции бетонного сечения относительно центра тяжести приведенного поперечного сечения элемента

J_red = J = b_t h_t³ / 12 (12.10)

Момент инерции площадей сечения растянутой и сжатой арматуры относительно центра тяжести приведенного поперечного сечения элемента

J_s ⁼ A_s (h₀ - y_c)² (12.11)

J '_s = A_s (y_c - a ')² (12.12)

Коэффициент приведения растянутой и сжатой арматуры к бетону

α = E_s / E_b1 (12.13)

Здесь Е_b1 определяют по аналогии с формулой (12.8).

Расстояние от наиболее сжатого волокна бетона до центра тяжести приведенного поперечного сечения элемента определяют по формуле:

y _s = S_c,red / A_red (12.14)

где S_c,red - статический момент приведенного сечения элемента относительно наиболее сжатого волокна бетона, равный:

S_c,red = S_c + S_sc α + S '_sc α (12.15)

Площадь приведенного поперечного сечения элемента равна

A_red = A + A_s α + A'_s α, (12.16)

где А - площадь бетонного сечения, определяемая по формуле (8.5) или (8.7), статический момент которой относительно наиболее сжатого волокна бетона определяется по формулам

S _c = A 0,5 h_t; (12.17)

S _sc = A_s h₀; (12.18)

S '_sc = A'_s a', (12.19)

где A_s, S_sc, A '_s, S '_sc - площади поперечного сечения и их статические моменты относительно наиболее сжатого волокна бетона соответственно растянутой и сжатой арматуры. Коэффициент приведения арматуры к бетону определяют по формуле (12.13).

12.12 Жесткость железобетонного элемента с трещиной в растянутой зоне определяют с учетом следующих положений:

- сечения после деформирования остаются плоскими;

- напряжения в бетоне в сжатой зоне определяют как для упругого бетона;

- работу растянутого бетона в сечении с нормальной трещиной не учитывают;

- работу растянутого бетона на участке между смежными нормальными трещинами учитывают коэффициентом ψ_s.

Жесткость железобетонного элемента на участке с трещинами в растянутой зоне принимают не более жесткости без трещин.

Жесткость железобетонного элемента D с трещинами в растянутой зоне определяют по формуле (12.7), в которой момент инерции J _red приведенного поперечного сечения элемента относительно его центра тяжести определяют по формуле (12.20) с учетом площади сжатой зоны, площадей сечения сжатой арматуры с коэффициентом приведения арматуры к бетону α_s1 и растянутой арматуры с коэффициентом приведения арматуры к бетону α_s2

J_red = J_b + J_s α_s1 + J' _s α_s2 (12.20)

12.13 Момент инерции площади сечения сжатого бетона J_b определяют:

а) при действии только изгибающего момента М:

для элементов прямоугольного поперечного сечения

J _b = b_t x_m³ / 3; (12.21)

для элементов таврового со сжатой полкой и двутаврового поперечных сечений с нулевой линией, расположенной в ребре ниже сжатой полки (х_т > h_ft), по формуле

(12.22)

 

б) при действии изгибающего момента М и продольной сжимающей или растягивающей силы N:

для элементов прямоугольного поперечного сечения по формуле

(12.23)

_{0588S10-01164}

для элементов таврового со сжатой полкой и двутаврового поперечных сечений с нулевой линией, расположенной в ребре ниже сжатой полки (х_т > h'_f), по формуле

(12.24)

_{0588S10-01164}

В тех случаях, когда в формулах (12.22) и (12.24) высота сжатой зоны x_m ≤ h'_ft, то момент инерции J_b вычисляют по формулам (12.21) и (12.23) как для прямоугольного сечения, принимая b_t = b'_ft.

12.14 Моменты инерции площадей сечения растянутой J_s и сжатой арматуры J' _s относительно центра тяжести приведенного поперечного сечения определяют по формулам

J_s = A_s (h₀ - y_cm)² (12.25)

J'_s = A'_s (y_cm - a')² (12.26)

Значение у_ст, равное расстоянию от наиболее сжатого волокна бетона до центра тяжести приведенного поперечного сечения без учета бетона растянутой зоны, для изгибаемых элементов равно х _т - средней высоте сжатой зоны бетона, учитывающей влияние работы растянутого бетона между трещинами, определяемой по формулам (12.27) и (12.30).

12.15 Для изгибаемых элементов высоту сжатой зоны х_т определяют по формуле

(12.27)

_{0588S10-01164}

где

	(12.28)
	(12.29)

Если вычисленная по формуле (11.27) высота сжатой зоны х_т ≤ h'_ft то расчет производят как для элементов прямоугольного поперечного сечения, принимая ширину сечения b = b'_f, a первый член в формулах (11.28) и (11.29) равным 0.

Для элементов прямоугольного сечения без сжатой арматуры высоту сжатой зоны х_т определяют по формуле

(12.30)

 

_{0588S10-01164}

где μ_s = A_s / b_t h₀.

12.16 Значения коэффициентов приведения арматуры к бетону принимают равными

для сжатой арматуры

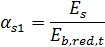
(12.31)

для растянутой арматуры

(12.32)

Значение коэффициента ψ_s для изгибаемых элементов допускается определять по формуле (12.33) без учета арматуры

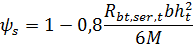
(12.33)

_{0588S10-01164}

Значение приведенного модуля деформации сжатого бетона E_b,red,t определяют по формуле (5.7) по температуре крайнего сжатого волокна бетона. Прочность бетона на растяжение R_bt,ser,t определяют по формуле (5.2) по температуре бетона на уровне растянутой арматуры.

12.17 Для элементов прямоугольного сечения среднюю высоту сжатой зоны х_т при действии изгибающего момента М и продольной силы N допускается определять по формуле

(12.34)

при этом принимают 0 ≤  х_т ≤  h_t.

В формуле (12.34) значение х_т1 вычисляют как для изгибаемых элементов по формулам (12.27) и (12.28).

В формуле (12.34) знак «плюс» принимают при сжимающей силе, знак «минус» - при растягивающей силе.

12.18 Кривизну элемента при остывании от температурной усадки неравномерно нагретого бетона во время пожара определяют по формуле:

(1/r)_cs = (α_cs1 t_b1 - α_cs t_b) / h, (12.35)

где α_cs1 и α_cs - коэффициенты температурной усадки бетона, принимаемые по табл. 5.3 в зависимости от температуры бетона более t_b1 и менее t_b нагретой грани сечения, которая была при пожаре.

12.19 После пожара прогиб элемента является одним из критериев возможности дальнейшей эксплуатации конструкции. При действии постоянных и длительных временных нагрузок прогиб балок, плит во всех случаях не должен превышать 1/150 пролета и 1/75 вылета консоли.

Если фактические прогибы превышают допустимые значения, но не препятствуют нормальной эксплуатации, допускается дальнейшая эксплуатация железобетонных конструкций без их усиления.

12.20 Определение прогибов железобетонных элементов на основе деформационной модели после пожара производится по формуле (12.4). Значения кривизны, входящие в формулу (12.5), определяют из решения уравнений железобетонных характеристик в охлажденном состоянии с учетом влияния температуры пожара на модуль упругости и деформации бетона согласно п.п. 8.25 - 8.27.

Модуль упругости арматуры после воздействия высокой температуры полностью восстанавливается. После пожара учитывают дополнительные напряжения сжатия, возникающие в арматуре от развития деформаций усадки в бетоне. Для этого следует прибавить к определяемой деформации бетона сжатию ε_b2 деформацию укорочения бетона от температурной усадки ε_cs менее нагретой части сечения

εcs = αcs tb

(12.36)

где α_cs - коэффициент температурной усадки бетона, принимаемый по табл. 5.3 в зависимости от температуры менее нагретой части сечения элемента t _b.

При двухзначной эпюре деформаций значение кривизны по сечению равно

(12.37)

Максимальные деформации бетона ε_b,тах определяют на основе положений, приведенных в п.п. 8.25 - 8.27.

Для элементов с трещинами в растянутой зоне напряжение в арматуре, пересекающей трещину, определяют по формуле

σsi = Es εsi,

(12.38)

где ε_si - усредненная относительная деформация растянутой арматуры в рассматриваемой стадии расчета, соответствующая линейному закону распределения деформаций по сечению.

---

Дата добавления: 2019-09-13; просмотров: 284; Мы поможем в написании вашей работы!

Поделиться с друзьями:

---

---

Мы поможем в написании ваших работ!