РАЗЛОЖЕНИЕ РАЦИОНАЛЬНОЙ ДРОБИ
КОМПЛЕКСНЫЕ ЧИСЛА
АЛГЕБРАИЧЕСКАЯ ФОРМА ЗАПИСИ
КОМПЛЕКСНОГО ЧИСЛА
О п р е д е л е н и е 1. Алгебраической формой записи комплексного числа  называется его представление в виде:
называется его представление в виде:
 (1)
(1)
где  вещественные числа, называемые, соответственно, вещественной частью (обозначают Re z) и мнимой частью (обозначают Im z) комплексного числа
вещественные числа, называемые, соответственно, вещественной частью (обозначают Re z) и мнимой частью (обозначают Im z) комплексного числа  число i, называемое мнимой единицей, определяется равенством
число i, называемое мнимой единицей, определяется равенством 
Множество всех комплексных чисел обозначают C.
З а м е ч а н и е 1. Любое вещественное число  является комплексным, так как его можно представить в виде (1):
является комплексным, так как его можно представить в виде (1):
 .
.
Следовательно,  Причем для вещественного числа
Причем для вещественного числа 
Re  =
=  , Im
, Im  = 0.
= 0.
О п р е д е л е н и е 2. Два комплексных числа
 и
и 
называются равными, если равны, соответственно, их вещественные и мнимые части:

О п р е д е л е н и е 3. Комплексное число, обозначаемое  и вычисляемое по формуле
и вычисляемое по формуле
 (2)
(2)
называется комплексно – сопряженным для числа  .
.
З а м е ч а н и е 2. Для геометрического представления комплексного числа вводят на плоскости прямоугольную систему координат  Тогда число
Тогда число  рассматривают как точку
рассматривают как точку  этой плоскости (рис.1) или же как радиус-вектор
этой плоскости (рис.1) или же как радиус-вектор  (рис.2).
(рис.2).
|
|
|









 b M b M
b M b M


О a х О a х
Рис. 1 Рис. 2
Операции над комплексными числами
 и
и 
1)  ;
;
2) 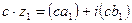 , где с - вещественное число;
, где с - вещественное число;
3)  ;
;
4)  .
.
З а м е ч а н и е 3. Для комплексно–сопряженных чисел справедливы равенства:

ТРИГОНОМЕТРИЧЕСКАЯ ФОРМА ЗАПИСИ КОМПЛЕКСНОГО ЧИСЛА
О п р е д е л е н и е 4. Тригонометрической формой записи комплексного числа  называется его представление в виде:
называется его представление в виде:
 , (3)
, (3)
где  неотрицательное вещественное число, называемое модулем комплексного числа
неотрицательное вещественное число, называемое модулем комплексного числа  и обозначаемое
и обозначаемое  ;
;  угол (
угол (  ), называемый главным значением аргумента комплексного числа
), называемый главным значением аргумента комплексного числа  и обозначаемый
и обозначаемый  (рис.3).
(рис.3).
 у Для комплексного числа
у Для комплексного числа 
справедливы соотношения:
|
|
|



 b z
b z

 r
r 
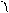
 j
j 
 .
.
0 a х
Рис. 3
Следовательно,
 и
и 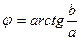 при
при 
 при
при 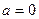 .
.
З а м е ч а н и е 4. Формула (3) верна при замене в ней  на
на  где
где  любое целое число.
любое целое число.
ПОКАЗАТЕЛЬНАЯ ФОРМА ЗАПИСИ
КОМПЛЕКСНОГО ЧИСЛА
О п р е д е л е н и е 5. Показательной формой записи комплексного числа  называется его представление в виде:
называется его представление в виде:
 , (4)
, (4)
где 
 ,
, 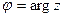 ,
,  .
.
Операции над комплексными числами
 и
и 
1) 
2) 
3) 
4)  где
где 
то есть: 
С геометрической точки зрения операции над комплексными числами выполняются по следующим правилам
(рис. 4 – 11):


 Сложение
Сложение  Вычитание
Вычитание




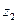
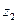
 | |||
 | |||




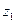
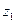
|
|
|



 О
О  О
О 
Рис. 4  Рис. 5
Рис. 5
Умножение на число a 



 (при
(при 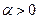 )
)

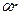




О 

 (при
(при  ) Рис.6
) Рис.6


 Умножение
Умножение  Деление
Деление



















|
|
|







 О
О  О
О 



Рис. 7 Рис. 8
Возведение в степень








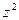







 |
О 
Рис. 9
Извлечение корня п-й степени из числа 
 у
у 
 | |||
 | |||








 (2p)/n
(2p)/n 
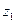










 j (2p)/n j/n (2p)/n х
j (2p)/n j/n (2p)/n х

 О
О
О 
 |
 Рис. 10
Рис. 10 
Рис. 11
РАЗЛОЖЕНИЕ МНОГОЧЛЕНА НА МНОЖИТЕЛИ
О п р е д е л е н и е 6. Многочленом от  степени
степени  (или целой рациональной функцией от
(или целой рациональной функцией от  ) называется функция вида
) называется функция вида
 , (5)
, (5)
где 
 действительные числа,
действительные числа,  - независимая переменная, которая может принимать любые комплексные значения.
- независимая переменная, которая может принимать любые комплексные значения.
О п р е д е л е н и е 7. Корнем многочлена (5) называется то значение переменной  , при котором многочлен (5) обращается в нуль.
, при котором многочлен (5) обращается в нуль.
Т е о р е м а 1 . Всякий многочлен степени  имеет ровно
имеет ровно  комплексных корней
комплексных корней  и может быть представлен в виде разложения на линейные множители:
и может быть представлен в виде разложения на линейные множители:
 (6)
(6)
О п р е д е л е н и е 8. Говорят, что корень 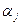 имеет кратность
имеет кратность  , если множитель
, если множитель  входит в разложение (6)
входит в разложение (6)  раз.
раз.
С в о й с т в о 1 . Если многочлен (5) имеет комплексный корень  (где
(где  ) кратности
) кратности  , то этот многочлен имеет также сопряженный корень
, то этот многочлен имеет также сопряженный корень  , кратность которого равна
, кратность которого равна  .
.
С в о й с т в о 2 . Если оставить в перечне корней многочлена (5) только различные корни и учесть их кратность, то многочлен (5) можно представить в виде произведения:

где
 ,
,
числа  (
(  ),
), 
 в разложении (7) являются вещественными, причем
в разложении (7) являются вещественными, причем
 (
(  );
);



РАЗЛОЖЕНИЕ РАЦИОНАЛЬНОЙ ДРОБИ
О п р е д е л е н и е 9. Рациональной дробью называется выражение вида:

где 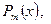
 многочлены по
многочлены по  степеней
степеней 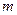 и
и  соответственно.
соответственно.
О п р е д е л е н и е 10. Рациональная дробь  называется правильной, если
называется правильной, если  В противном случае, если
В противном случае, если  она называется неправильной.
она называется неправильной.
О п р е д е л е н и е 11. Простейшими рациональными дробями называются дроби следующих четырех типов:
I.  ;
;
II.  ;
;
III.  ;
;
IV. 
 .
.
Т е о р е м а 2.Всякая неправильная рациональная дробь представима в виде суммы многочлена (ее целой части) и правильной рациональной дроби.
З а м е ч а н и е 5. Такого представления можно достичь, например, с помощью деления многочленов  на
на 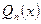 «в столбик», прекращая процедуру деления как только степень многочлена, сформировавшегося в остатке, станет меньше степени многочлена
«в столбик», прекращая процедуру деления как только степень многочлена, сформировавшегося в остатке, станет меньше степени многочлена 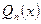 .
.
Т е о р е м а 3. Всякую правильную рациональную дробь можно представить в виде суммы конечного числа простейших рациональных дробей.
З а м е ч а н и е 6. На практике осуществить разложение правильной рациональной дроби  на сумму простейших рациональных дробей можно по следующей с х е м е:
на сумму простейших рациональных дробей можно по следующей с х е м е:
¨ Найти корни многочлена
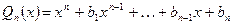
и представить его в виде разложения на множители:

где  ;
;


 ;
;
¨ Записать разложение с неопределенными коэффициентами:



 , (8)
, (8)
содержащее  слагаемых;
слагаемых;
¨ Определить коэффициенты

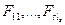 ,
,
суммарное число которых равно  .
.
З а м е ч а н и е 7. Определить коэффициенты разложения (8) можно многими способами. Например, приведя (8) к общему знаменателю, получим равенство двух многочленов. Приравнивая в них коэффициенты при одинаковых степенях  , получим систему
, получим систему  линейных уравнений с
линейных уравнений с  интересующими нас неизвестными, имеющую единственное решение. Такой метод называют методом неопределенных коэффициентов.
интересующими нас неизвестными, имеющую единственное решение. Такой метод называют методом неопределенных коэффициентов.
З а м е ч а н и е 8. Метод неопределенных коэффициентов приводит к цели всегда, но является довольно громоздким.
В ряде случаев удается определить коэффициенты, участвующие в разложении дроби на сумму простейших рациональных дробей, более простым способом, носящим название метода зачеркивания. Изложим его суть.
Пусть знаменатель правильной рациональной дроби

имеет вещественное число  своим корнем кратности
своим корнем кратности  .
.
В этом случае среди простейших дробей, на сумму которых разлагается дробь  , будет фигурировать дробь
, будет фигурировать дробь  , а многочлен
, а многочлен  будет представим в виде:
будет представим в виде:
 ,
,
где  многочлен по
многочлен по  степени
степени  , причем
, причем 
Тогда коэффициент  равен:
равен:
 .
.
Таким образом, для вычисления коэффициента  следует в знаменателе исходной дроби
следует в знаменателе исходной дроби  «зачеркнуть» скобку
«зачеркнуть» скобку  и в оставшееся выражение подставить
и в оставшееся выражение подставить  .
.
ПРИМЕРЫ С РЕШЕНИЯМИ
П р и м е р 1. Выполнить указанные действия:
а)  б)
б)  в)
в) 
Р е ш е н и е. Воспользовавшись правилами сложения, умножения, деления комплексных чисел, заданных в алгебраической форме, получаем:
а) 
б) 
в) 
О т в е т: а)  б)
б)  в)
в) 
П р и м е р 2. Решить уравнения:
а)  б)
б) 
Р е ш е н и е. Воспользовавшись формулой корней квадратного уравнения, получаем:
а)


б)
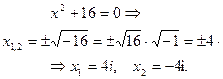 i
i 
О т в е т: а) 
б) 
П р и м е р 3. Представить комплексные числа
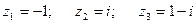
в тригонометрической форме.
Р е ш е н и е. Изобразим данные числа на комплексной плоскости (рис. 12). Для числа  находим модуль и аргумент:
находим модуль и аргумент:

 .
. 

 1 Следовательно, по формуле (3)
1 Следовательно, по формуле (3)
 получаем:
получаем:



 -1 О 1 х
-1 О 1 х 

 -1
-1 
Рис. 12
Аналогично находим:


Следовательно, справедливы представления:
 ,
, 
О т в е т:  ,
,  ,
,

П р и м е р 4. Вычислить:
а)  б)
б) 
Р е ш е н и е. Воспользовавшись правилами возведения в степень и извлечения корня из комплексных чисел, заданных в показательной форме, получаем:
а) 
= 
б) 

Следовательно, заключаем:
при 
при 
при 
при 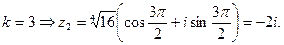
О т в е т: а) 16; б) 2, -2, 2i, -2i.
П р и м е р 5. Определить, какие из указанных рациональных дробей являются правильными:
а)  б)
б) 
в)  .
.
Р е ш е н и е. а) Дробь является неправильной, так как степени многочленов, стоящих в числителе и знаменателе, совпадают (равны четырем).
б) – в) Дроби являются правильными, так как в числителе стоит многочлен степени 4, а знаменателе – степени 5 в б) и 6 в в).
О т в е т: б), в).
П р и м е р Неправильную рациональную дробь  заменить суммой многочлена и правильной рациональной дроби, если
заменить суммой многочлена и правильной рациональной дроби, если
а) 
б) 
Р е ш е н и е. Разделим многочлен  на многочлен
на многочлен  :
:
 а)
а) 







 ,
,
следовательно
 ;
;
 б)
б) 
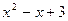



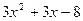









 ,
,
следовательно 
О т в е т: а) 
б) 
П р и м е р 7. Разложить на множители многочлен
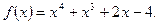
Р е ш е н и е. Вещественный целый корень многочлена  следует искать среди целых делителей числа 4 - свободного члена многочлена
следует искать среди целых делителей числа 4 - свободного члена многочлена  . Ими являются числа
. Ими являются числа 
Вычислим значения многочлена  при указанных значениях
при указанных значениях  :
:

Следовательно, числа  являются корнями многочлена
являются корнями многочлена  . Отсюда вытекает справедливость представления:
. Отсюда вытекает справедливость представления:
 , (9)
, (9)
где  некоторый многочлен.
некоторый многочлен.
Найдем многочлен  , разделив
, разделив  на многочлен
на многочлен  , то есть на квадратный трехчлен
, то есть на квадратный трехчлен 






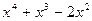


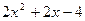

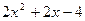
0.
Итак, вычисления показали, что в формуле (4)  =
=  , причем
, причем 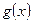 не разлагается на линейные множители с вещественными коэффициентами (так как дискриминант этого квадратного трехчлена меньше нуля). Следовательно, из равенства (9), получаем:
не разлагается на линейные множители с вещественными коэффициентами (так как дискриминант этого квадратного трехчлена меньше нуля). Следовательно, из равенства (9), получаем:  .
.
О т в е т:  .
.
П р и м е р 8. Написать разложение дроби

на сумму простейших рациональных дробей, не находя коэффициентов разложения.
О т в е т:


П р и м е р Разложить дробь на сумму простейших рациональных дробей и найти коэффициенты разложения:
а)  ; б)
; б) 
в) 
Р е ш е н и е. а) Дробь  является правильной. Для ее знаменателя справедливо представление:
является правильной. Для ее знаменателя справедливо представление:

Запишем разложение дроби на сумму простейших рациональных дробей с неопределенными коэффициентами:
 . (10)
. (10)
Найдем коэффициенты разложения (10) методом неопределенных коэффициентов.
Приведем равенство (10) к общему знаменателю и приравняем числители получившихся при этом дробей:


Отсюда, приравнивая коэффициенты при одинаковых степенях  , приходим к системе:
, приходим к системе:
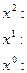


Следовательно, подставляя найденные числа А, В, С в разложение (10), приходим к равенству:
 =
=  .
.
Покажем, как числа  можно было найти из формулы (10) методом зачеркивания:
можно было найти из формулы (10) методом зачеркивания:
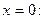





б) Дробь  - правильная. Знаменатель этой дроби имеет вид:
- правильная. Знаменатель этой дроби имеет вид:

Поэтому справедливо разложение:

=  . (11)
. (11)
Коэффициенты А, В этого разложения найдем методом зачеркивания:
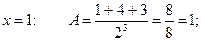

Для поиска коэффициентов C и D подставим в (11) вместо x любые два числа (кроме тех, которые уже были использованы).
Например:

Отсюда для поиска коэффициентов C и D получаем систему:

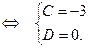
Подставив найденные числа А, В, С, D в разложение (11), приходим к равенству:

в) Дробь  - правильная. Ее знаменатель имеет вид:
- правильная. Ее знаменатель имеет вид:

причем у квадратного трехчлена  дискриминант меньше нуля, и он не разлагается на линейные множители с вещественными коэффициентами.
дискриминант меньше нуля, и он не разлагается на линейные множители с вещественными коэффициентами.
Поэтому справедливо представление:

 (12)
(12)
Методом зачеркивания находим число А:

Для поиска коэффициентов B, C, D приведем (12) к общему знаменателю и приравняем числители:

Используем правило: многочлены равны, если равны коэффициенты при одинаковых степенях  . Это приводит к системе:
. Это приводит к системе:
 .
.
Отсюда получаем:



Подставив найденные числа А, В, С, D в разложение (12), приходим к равенству:


О т в е т: а) 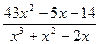 =
=  ;
;
б) 
в) 

П Р И М Е Р Ы
1. Выполнить указанные действия:
а)  б)
б) 
в)  г)
г)  д)
д) 
е)  ж)
ж)  з)
з) 
и)  к)
к)  л)
л) 
2. Представить в тригонометрической форме числа:
а) 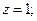
б) 
в) 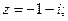
г) 
3. Решить квадратное уравнение:
а)  б)
б) 
в) 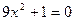 г)
г) 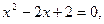
д)  , е)
, е) 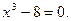
Разложить дроби на сумму простейших дробей:
4.  . 5.
. 5.  .
.
6.  . 7.
. 7.  .
.
8.  . 9.
. 9.  .
.
10.  . 11.
. 11.  .
.
♦ ♦ ♦
12. Представить в тригонометрической форме числа:
а)  б)
б) 
в) 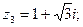 г)
г) 
д) 
13. Выполнить действия:
а)  б)
б) 
в)  г)
г)  д)
д) 
е) 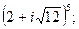 ж)
ж)  з)
з) 
14. Решить уравнения:
а) 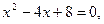 б)
б) 
в)  г)
г) 
д)  .
.
Разложить дроби на сумму простейших дробей,
не находя коэффициентов разложения :
15.  16.
16. 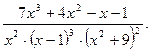
Разложить дроби на сумму простейших дробей:
17.  . 18.
. 18.  .
.
19. 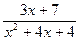 . 20.
. 20. 
21.  22.
22. 
23. 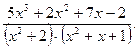 24.
24. 
О Т В Е Т Ы
1. а)  б)
б)  в)
в)  г)
г) 
д)  е)
е)  ж)
ж)  з)
з) 
и)  к)
к) 


л) 
2. а)  ; б)
; б)  ;
;
в) 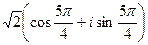 ; г)
; г) 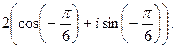
3. а) 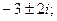 б)
б)  в)
в)  ; г)
; г) 
д)  е)
е) 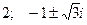 .
.
4.  5.
5.  6.
6.  .
.
7.  8.
8.  9.
9. 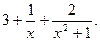
10.  11.
11.  .
.
12. а)  б)
б) 

в) 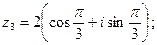 г)
г) 

д) 
13. а)  б)
б) 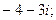 в)
в)  г)
г) 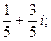 д)
д) 
е)  ж)
ж) 

з) 


14. а)  б)
б) 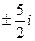 ; в)
; в) 
г)  е)
е)  .
.
15. 

16. 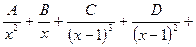

17.  18.
18. 
19.  . 20.
. 20. 
21.  22.
22. 
23. 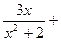
 24. 1+
24. 1+ 
Дата добавления: 2019-09-13; просмотров: 110; Мы поможем в написании вашей работы! |

Мы поможем в написании ваших работ!
