Бимедианы четырехугольника и отрезок, соединяющий середины диагоналей, пересекаются в одной точке и делятся этой точкой пополам.
Муниципальное общеобразовательное учреждение
«Средняя общеобразовательная школа №24»
Параллелограмм Вариньона
Выполнил: Сабитов Тимур Ильясович
ученик 8 Б кл. МОУ «СОШ № 24»
Руководитель: Шамраева Оксана Викторовна
учитель математики
г.Абакан 2011 год
Содержание
Содержание……………………………………………………………………… ..2
1. Введение………………………………………………………………………. .3
2. Историческая справка………………………………………………………….. 4
3. Теорема Вариньона
3.1. Параллелограмм Вариньона................................................................. 5
3.2. Следствие 1........................................................................................... 6
3.3 Следствие 2............................................................................................. 8
3.4 Следствие 3............................................................................................. 9
3.5 Следствие4....................................... .....................................................10
4. Сравнительный анализ двух решений одной задачи.......................................11
5. Разбор задач......................................................................................................... 12
Заключение.............................................................................................................. 16
Список литературы................................................................................................. 17
2
1. Введение.
Крупное научное открытие дает
решение крупной проблемы,
но и в решении любой задачи
присутствует крупица открытия.
|
|
|
Д. Пойа (венгерский математик)
В математике самыми трудными считаются геометрические задачи. Почти каждая геометрическая задача нестандартна. Надо подумать, какие нужно сделать дополнительные построения, какими воспользоваться теоремами, при этом очень непросто из их огромного количества выбрать ту, которая наилучшим образом поможет в решении.
Цель работы: показать, что теорема Вариньона — надёжный помощник в решении геометрических задач.
Актуальность и новизна работы состоит в том, что область применения теоремы Вариньона не раскрыта в школьных учебниках и не показана её роль в решении задач.
Задачи работы:
1. Рассмотреть доказательство теоремы Вариньона для выпуклого четырехугольника.
2. Продемонстрировать применение теоремы Вариньона для решения важных планиметрических задач.
Методы исследования:
1. Анализ, систематизация и обобщение данных из различных источников информации
2. Самостоятельное решение задач.
3
Историческая справка
|

|
|
|
4
3. Теорема Вариньона
3.1. Параллелограмм Вариньона
Теорема Вариньона вытекает из теоремы о средней линии треугольника: средняя линия треугольника параллельна одной из его сторон и равна половине этой стороны и гласит: середины сторон произвольного четырёхугольника являются вершинами параллелограмма.
Рассмотрим доказательство теоремы.



Доказательство:

1) К и L – середины сторон АD и AB, значит КL – средняя линия треугольника
АВD, поэтому отрезок КL параллелен
диагонали BD и равен её половине.
2) M и N – середины сторон BC и CD, значит MN – средняя линия треугольника BDС, поэтому отрезок MN параллелен диагонали BD и равен её половине.
|
|
|
3) Таким образом, MN || KL и KL = MN , значит четырехугольник KLMN –
параллелограмм по признаку. Теорема доказана.
Рис. 1
Свойства параллелограмма Вариньона:
1. Стороны этого параллелограмма параллельны диагоналям четырёхугольника, а их длины равны половинам длин диагоналей.
2. Площадь параллелограмма Вариньона равна половине площади исходного четырехугольника.
3. Сумма квадратов диагоналей равна сумме квадратов сторон
5
3.2. Следствие 1.
1. Параллелограмм Вариньона является ромбом, когда в исходном четырехугольнике:
а) диагонали равны (см. рис. 2,а);
б) бимедианы (отрезки, соединяющие середины противоположных сторон) перпендикулярны (см. рис. 2,б).


Рис. 2 а) Рис. 2 б)
Доказательство:
а) Так как диагонали исходного четырехугольника равны, то стороны параллелограмма Вариньона будут равны (по свойству средней линии треугольника). Параллелограмм Вариньона является ромбом (по признаку ромба).
|
|
|
б) Бимедианы исходного четырехугольника – это диагонали параллелограмма Вариньона. Так как в параллелограмме диагонали перпендикулярны, то этот параллелограмм является ромбом (по признаку ромба).
2. Параллелограмм Вариньона является прямоугольником, когда в исходном четырехугольнике:
а) диагонали перпендикулярны (см. рис. 3,а);
б) бимедианы равны (см. рис. 3,б).


Рис. 3 а) Рис. 3 б)
Доказательство:
а) Так как диагонали исходного четырехугольника перпендикулярны, то
6
стороны параллелограмма Вариньона будут перпендикулярны. Тогда параллелограмм Вариньона является прямоугольником (по признаку прямоугольника).
б) Бимедианы исходного четырехугольника – это диагонали параллелограмма Вариньона. Так как в параллелограмме диагонали равны, то этот параллелограмм является прямоугольником (по признаку прямоугольника).
Параллелограмм Вариньона является квадратом, когда в исходном четырехугольнике:
а) диагонали равны и перпендикулярны(см. рис. 4,а);
б) бимедианы равны и перпендикулярны (см. рис. 4,б).


Рис. 4 а) Рис. 4 б)
Доказательство:
а) Так как диагонали исходного четырехугольника равны и перпендикулярны, то стороны параллелограмма Вариньона будут равны и перпендикулярны. Тогда параллелограмм Вариньона является квадратом (по признаку квадрата).
б) Бимедианы исходного четырехугольника – это диагонали параллелограмма Вариньона. Так как в параллелограмме диагонали равны и перпендикулярны, то этот параллелограмм является квадратом (по признаку квадрата).
7
3.3 Следствие 2.
Бимедианы четырехугольника и отрезок, соединяющий середины диагоналей, пересекаются в одной точке и делятся этой точкой пополам.
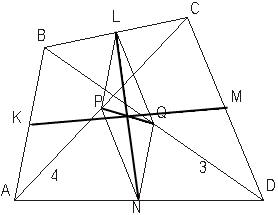
Рис 5
Доказательство:
Пусть KM и LN – бимедианы ABCD, PQ – отрезок, соединяющий середины диагоналей АС и BD.
1) Т.к. KM и LN являются диагоналями параллелограмма Вариньона ⇒ KM и LN
точкой пересечения делятся пополам. Поэтому нам достаточно доказать, что отрезки PQ и LN их точкой пересечения делятся пополам (рис.5).
2) Рассмотрим ∆DBC и ∆ ACD, у них
CD – общее основание, LQ║CD и PN║CD (по теореме о средней линии треугольника)  LQ║PN.
LQ║PN.
Рассмотрим ∆ABC и ∆ABD, у них
AB – общее основание, PL║AB и NQ║AB (по теореме о средней линии треугольника)  PL║NQ
PL║NQ
3) LQ║PN, PL║NQ  PLQN – параллелограмм. По свойству параллелограмма следует, что отрезки PQ и LN их точкой пересечения делятся пополам. Что и требовалось доказать.
PLQN – параллелограмм. По свойству параллелограмма следует, что отрезки PQ и LN их точкой пересечения делятся пополам. Что и требовалось доказать.
8
3.4 Следствие 3.
Для четырехугольника сумма квадратов всех сторон равна сумме квадратов диагоналей плюс учетверенный квадрат отрезка, соединяющего середины диагоналей, то есть  .
.
Доказательство.

Рис.6
Уже было отмечено что LPNQ – параллелограмм (см. доказательство след. 2)
Поэтому по свойству параллелограмма Вариньона
1)  ;
;
В последнем равенстве мы дважды воспользовались теоремой о средней линии треугольника. Аналогично для параллелограмма KPMQ имеем:
 .
.
Кроме того, по свойству параллелограмма Вариньона
 ,
,
Складывая первые два равенства и учитывая последнее, получаем соотношение Эйлера:

 │∙2
│∙2

9
3.5 Следствие 4.
Суммы площадей накрест лежащих четырехугольников, образованных пересечением бимедиан LN и KM выпуклого четырехугольника ABCD равны. Доказательство.

1) ∆KBL ~ ∆ABC (по двум сторонам и углу между ними) ⇒

2) Аналогично:
∆DNM ~ ∆DAC 

3) 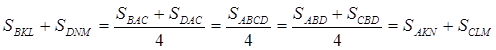
4)  ∙
∙  ,
,  ∙
∙  , т.к. KO=OM
, т.к. KO=OM 

5) Аналогично:

6) Сложим получившиеся равенства, получаем:

Что и требовалось доказать.
10
Дата добавления: 2019-09-13; просмотров: 777; Мы поможем в написании вашей работы! |

Мы поможем в написании ваших работ!
