Требования к оформлению отчета
Отчет по лабораторной работе должен содержать следующие разделы:
1. титульный лист;
2. цель работы:
3. задание на лабораторную работу;
4. ход работы;
5. ответы на контрольные вопросы;
6. выводы по проделанной работе.
Задание на работу
Реализуйте дерево целых чисел, добавление и удаление листьев.
· Создайте процедуру обхода дерева «в глубину».
· Создайте процедуру обхода дерева «в ширину».
· Создайте процедуру поиска значения.
· Создайте процедуру построения бинарного дерева на основе не бинарного.
· Создайте процедруру обхода дерева с использованием пустых указателей в исходном дереве для организации перехода от «потомков» к «предкам».
· Создайте процедуру обхода дерева с использованием изменения внутренней структуры дерева для определения пути обхода?
Контрольные вопросы
- Что такое дерево?
- Какие есть способы задания бинарных деревьев?
- Какие есть способы задания не бинарных деревьев?
- Какие виды обхода вы значете? В чем разница между обходом «сверзу вниз» и «снизу вверх»?
- Опишите основные принципы обхода «в глубину».
- Опишите основные принципы обхода «в ширину».
Лабораторная работа № 9.
Алгоритмические основы программирования на языке С++.
Задачи на графах
Цель работы
Ознакомится с графами и основными алгоритмами на них.
Теоретические сведения
Представление графов
Имеется два стандартных способа представления графа G = (V, E): как набора списков смежных вершин или как матрицы смежности. Оба способа предпредставления применимы как для ориентированных, так и для неориентированных графов. Обычно более предпочтительно представление с помощью списков смежности, поскольку оно обеспечивает компактное представление разреженных (sparse) графов, т.е. таких, для которых |Е| гораздо меньше |V|2. Представление при помощи матрицы смежности предпочтительнее в случае плотных (dense) графов, т.е. когда значение |E| близко к |V|2, или когда надо иметь возможность быстро определить, имеется ли ребро, соединяющее две данные вершины.
|
|
|
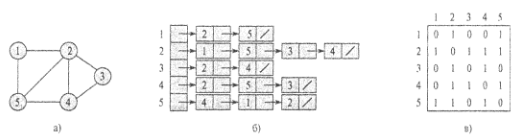
Рис. 21. Представление неориентированного графа.
а) исходный граф, б) список смежности, в)матрица смежности
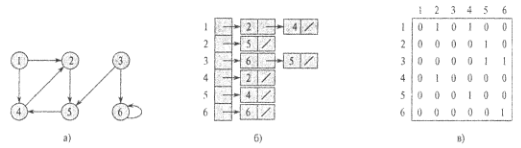
Рис. 22. Представление ориентированного графа.
а) исходный граф, б) список смежности, в)матрица смежности
Представление графа G = (V, Е) в виде списка смежности (adjacency-list representation) использует массив Adj из |V| списков, по одному для каждой вершины из V. Для каждой вершины u Є V список Adj [u] содержит все смежные вершины. Вершины в каждом списке обычно хранятся в произвольном порядке. На рис. 21б показано такое представление графа, изображенного на рис. 21а.
Если G — ориентированный граф, то сумма длин всех списков смежности равна |E| поскольку ребру (u,v) однозначно соответствует элемент v в списке Adj [u]. Если G — неориентированный граф, то сумма длин всех списков смежности равна 2|Е|, поскольку ребро (u,v), будучи неориентированным, появляется в списке Adj [v] как и, и в списке Adj [u] — как v. Как для ориентированных, так и для неориентированных графов представление в виде списков требует объем памяти, равный O (V + Е).
|
|
|
Списки смежности легко адаптируются для представления взвешенных графов (weighted graph), т.е. графов, с каждым ребром которых связан определенный вес (weight).
Например, пусть G = (V, Е) — взвешенный граф с весовой функцией w. Вес w (u, v) ребра (u, v) просто хранится вместе с вершиной v в списке смежности Adj[u]. Представление с помощью списков смежности достаточно гибко в том смысле, что легко адаптируется для поддержки многих других вариантов графов.
Потенциальный недостаток представления при помощи списков смежности заключается в том, что при этом нет более быстрого способа определить, имеется ли данное ребро (u, v) в графе, чем поиск v в списке Adj[u]. Этот недостаток можно устранить ценой использования асимптотически большего количества памяти и представления графа с помощью матрицы смежности.
|
|
|
Представление графа G = (V, Е) с помощью матрицы смежности (adjacency-matrix representation) предполагает, что вершины перенумерованы в некотором порядке числами 1,2,...,|V|. В таком случае представление графа G с использованием матрицы смежности представляет собой матрицу А = (аij) размером |V| х |V|, такую что a[i][j] = 1, если есть ребро (u,v) и 0, если ребра нет.
На рис. 21в и рис. 22в показаны представления с использованием матрицы смежности неориентированного и ориентированного графов. Обратите внимание на симметричность матрицы смежности на рис. 21в относительно главной диагонали. Поскольку граф неориентирован, (u, v) и (v, u) представляют одно и то же ребро, так что матрица смежности неориентированного графа совпадает с транспонированной матрицей смежности, т.е. А = АT. В ряде приложений это свойство позволяет хранить только элементы матрицы, находящиеся на главной диагонали и выше нее, что позволяет почти в два раза сократить необходимое количество памяти.
Так же, как и представление со списками смежности, представление с матрицами смежности можно использовать для взвешенных графов. Например, если G = (У, Е) — взвешенный граф с весовой функцией w, то вес w (и, v) ребра (u, v) хранится в записи в строке и столбце v матрицы смежности. Если ребро не существует, то в соответствующем элементе матрицы хранится значение NULL, хотя для многих приложений удобнее использовать некоторое значение, такое как 0 или «машинная бесконечность».
|
|
|
Хотя список смежности асимптотически, как минимум, столь же эффективен в плане требуемой памяти, как и матрица смежности, простота последней делает ее предпочтительной при работе с небольшими графами. Кроме того, в случае невзвешенных графов для представления одного ребра достаточно одного бита, что позволяет существенно сэкономить необходимую для представления память.
Поиск в ширину
Поиск в ширину (breadth-first search) представляет собой один из простейших алгоритмов для обхода графа и является основой для многих важных алгоритмов для работы с графами. Например, алгоритм Прима (Prim) поиска минимального остовного дерева или алгоритм Дейкстры (Dijkstra) поиска кратчайшего пути из одной вершины используют идеи, сходные с идеями, используемыми при поиске в ширину.
Пусть задан граф G = (V, Е) и выделена исходная (source) вершина s. Алгоритм поиска в ширину систематически обходит все ребра G для «открытия» всех вершин, достижимых из s, вычисляя при этом расстояние (минимальное количество ребер) от s до каждой достижимой из s вершины. Кроме того, в процессе обхода строится «дерево поиска в ширину» с корнем s, содержащее все достижимые вершины. Для каждой достижимой из s вершины v путь в дереве поиска в ширину соответствует кратчайшему (т.е. содержащему наименьшее количество ребер) пути от s до v в G. Алгоритм работает как для ориентированных, так и для неориентированных графов.
Поиск в ширину имеет такое название потому, что в процессе обхода мы идем вширь, т.е. перед тем как приступить к поиску вершин на расстоянии к +1, выполняется обход всех вершин на расстоянии к.
Для отслеживания работы алгоритма поиск в ширину раскрашивает вершины графа в белый, серый и черный цвета. Изначально все вершины белые, и позже они могут стать серыми, а затем черными. Когда вершина открывается (discovered) в процессе поиска, она окрашивается. Таким образом, серые и черные вершины - это вершины, которые уже были открыты, но алгоритм поиска в ширину по разному работает с ними, чтобы обеспечить объявленный порядок обхода. Если (u, v) Є Е и вершина u черного цвета, то вершина v либо серая, либо черная, т.е. все вершины, смежные с черной, уже открыты. Серые вершины могут иметь белых соседей, представляя собой границу между открытыми и неоткрытыми вершинами.
Поиск в ширину строит дерево поиска в ширину, которое изначально состоит из одного корня, которым является исходная вершина s. Если в процессе сканирования списка смежности уже открытой вершины и открывается белая вершина v, то вершина v и ребро (u, v) добавляются в дерево. Принято говорить, что u является предшественником (predecessor), или родителем (parent), v в дереве поиска вширь. Поскольку вершина может быть открыта не более одного раза, она имеет не более одного родителя. Взаимоотношения предков и потомков определяются в дереве поиска в ширину как обычно — если u находится на пути от корня s к вершине v, то u является предком v, а v — потомком u.
Приведенная ниже процедура поиска в ширину BFS предполагает, что входной граф G = (V, Е) представлен при помощи списков смежности. Кроме того, поддерживаются дополнительные структуры данных в каждой вершине графа. Цвет каждой вершины u Є V хранится в переменной u->color, а предшественник - в переменной u->prev. Если предшественника у u нет (например, если u == s или u не открыта), то u->prev = NULL. Расстояние от s до вершины u, вычисляемое алгоритмом, хранится в поле u->d. Алгоритм использует очередь Q для работы с множеством серых вершин:
// условные названия:
// queue - очередь
// enqueue - добавить в очередь
// get_next_vertex - получить следущую за u вершину в // графе G
// queue очередь из указателей
// create_queue - создать пустую очередь
/ enueue - добавить в очередь
// dequeue - удалить из очереди
BFS(graph *G, vertex *s){
0 vertex *u = NULL;
1 while ((u = get_next_vertex(G,u) != NULL)
2 u->color = White;
3 u->d = MAX_INT;
4 u->prev = NULL;
5 s->color = Gray;
6 s->d = 0;
7 s->prev = NULL;
8 queue Q = create_queue();
9 enqueue(Q,s);
10 while (!empty(Q)){
11 vertex *u = dequeue(Q);
12 while ((vertex *v = get_adj(u)) != NULL){
13 if (v->color == White){
14 v->color = Gray;
15 v->d = u->d + 1;
16 v->prev = u;
17 enqueue(Q,v);
}
18 u->color = Black;
}
}
}
На рис. 23 проиллюстрирована работа процедуры BFS. Внутри каждой вершины графа и приведено значение u->d, а состояние очереди Q показано на момент начала каждой итерации цикла while в строках 10-18. Рядом с элементами очереди показаны расстояния до корня.
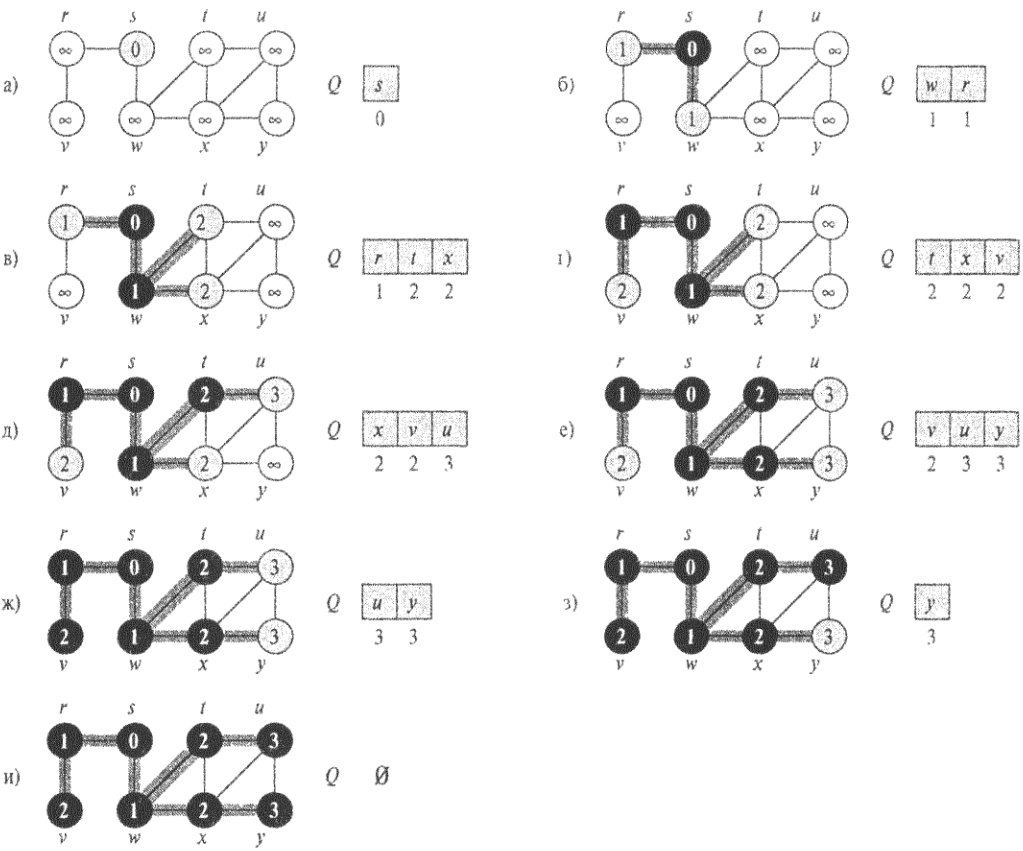
Рис. 23. Выполнение процедуры BFS над неориентированным графом
Процедура BFS работает следующим образом. В строках 1-4 все вершины, за исключением исходной вершины s, окрашиваются в белый цвет, для каждой вершины и полю u->d присваивается значение MAX_INT(=бесконечность), а в качестве родителя для каждой вершины устанавливается NULL. В строке 5 исходная вершина s окрашивается в серый цвет, поскольку она рассматривается как открытая в начале процедуры.
В строке 6 ее полю s->d присваивается значение 0, а в строке 7 ее родителем становится NULL. В строках 8-9 создается пустая очередь Q, в которую помещается один элемент s.
Цикл while в строках 10-18 выполняется до тех пор, пока остаются серые вершины (т.е. открытые, но списки смежности которых еще не просмотрены).
Инвариант данного цикла выглядит следующим образом:
При выполнении проверки в строке 10 очередь Q состоит из множества серых вершин.
Хотя мы не намерены использовать этот инвариант для доказательства корректности алгоритма, легко увидеть, что он выполняется перед первой итерацией и что каждая итерация цикла сохраняет инвариант. Перед первой итерацией единственной серой вершиной и единственной вершиной в очереди Q, является исходная вершина s. В строке 11 определяется серая вершина и в голове очереди Q, которая затем удаляется из очереди. Цикл for в строках 12-17 просматривает все вершины v в списке смежности и. Если вершина v белая, значит, она еще не открыта, и алгоритм открывает ее, выполняя строки 14-17. Вершине назначается серый цвет, дистанция v->d устанавливается равной v->d + 1, а в качестве ее родителя указывается вершина u. После этого вершина помещается в хвост очереди Q. После того как все вершины из списка смежности и просмотрены, вершине u присваивается черный цвет. Инвариант цикла сохраняется, так как все вершины, которые окрашиваются в серый цвет (строка 14), вносятся в очередь (строка 17), а вершина, которая удаляется из очереди (строка 11), окрашивается в черный цвет (строка 18).
Результат поиска в ширину может зависеть от порядка просмотра вершин, смежных с данной вершиной, в строке 12. Дерево поиска в ширину может варьироваться, но расстояния d, вычисленные алгоритмом, не зависят от порядка просмотра.
Поиск в глубину
Стратегия поиска в глубину, как следует из ее названия, состоит в том, чтобы идти «вглубь» графа, насколько это возможно. При выполнении поиска в глубину исследуются все ребра, выходящие из вершины, открытой последней, и покидает вершину, только когда не остается неисследованных ребер — при этом происходит возврат в вершину, из которой была открыта вершина v. Этот процесс продолжается до тех пор, пока не будут открыты все вершины, достижимые из исходной. Если при этом остаются неоткрытые вершины, то одна из них выбирается в качестве новой исходной вершины и поиск повторяется уже из нее. Этот процесс повторяется до тех пор, пока не будут открыты все вершины.
Как и в случае поиска в ширину, когда вершина v открывается в процессе сканирования списка смежности уже открытой вершины u, процедура поиска записывает это событие, устанавливая поле предшественника v v->prev равным u. В отличие от поиска в ширину, где подграф предшествования образует дерево, при поиске в глубину подграф предшествования может состоять из нескольких деревьев, так как поиск может выполняться из нескольких исходных вершин.
Подграф предшествования (predecessor subgraph) поиска в глубину, таким образом, несколько отличается от такового для поиска в ширину. Мы определяем его как граф Gπ = (V, Еπ), где
Eπ = {(v->prev, v): v Є V и v->prev != NULL}.
Подграф предшествования поиска в глубину образует лес поиска в глубину (depth-first forest), который состоит из нескольких деревьев поиска в глубину (depth-first-trees). Ребра в Еπ называются ребрами дерева (tree edges).
Как и в процессе выполнения поиска в ширину, вершины графа раскрашиваются в разные цвета, свидетельствующие о их состоянии. Каждая вершина изначально белая, затем при открытии (discover) в процессе поиска она окрашивается в серый цвет, и по завершении (finish), когда ее список смежности полностью сканирован, она становится черной. Такая методика гарантирует, что каждая вершина в конечном счете находится только в одном дереве поиска в глубину, так что деревья не пересекаются.
Помимо построения леса поиска в глубину, поиск в глубину также проставляет в вершинах метки времени (timestamp). Каждая вершина имеет две такие метки — первую v->d, в которой указывается, когда вершина v открывается (и окрашивается в серый цвет), и вторая - v->f которая фиксирует момент, когда поиск завершает сканирование списка смежности вершины у и она становится черной. Эти метки используются многими алгоритмами и полезны при рассмотрении поведения поиска в глубину.
Приведенная ниже процедура DFS записывает в поле u->d момент, когда вершина и открывается, а в поле u->f - момент завершения работы с вершиной u. Эти метки времени представляют собой целые числа в диапазоне от 1 до 2 |V|, поскольку для каждой из |V| вершин имеется только одно событие открытия и одно - завершения. Для каждой вершины u:
u->d < u->f
До момента времени u->d вершина имеет цвет white, между u->d и u->f - цвет gray, а после u->f - цвет black.
Далее представлен псевдокод алгоритма поиска в глубину. Входной граф G может быть как ориентированным, так и неориентированным. Переменная time - глобальная и используется нами для меток времени.
DFS(graph *G, vertex *s){
0 vertex *u = NULL;
1 while ((u = get_next_vertex(G,u) != NULL){
2 u->color = White;
3 u->prev = NULL;
}
4 time = 0;
vertex *u = NULL;
5 while ((u = get_next_vertex(G,u) != NULL){
6 if(u->color == White)
7 dfs_visit(u)
}
}
DFS_svisit(vertex *u){
1 u->color = Gray;
2 time++;
3 d->u = time;
4 while ((vertex *v = get_adj(u)) != NULL){
5 if(v->color == White){
6 v->prev = u;
7 DFS_visit(v0;
}
}
8 u->color = Black
9 u->f = time = time + 1;
}
На рис. 24 проиллюстрировано выполнение процедуры DFS над графом. Ребра, исследованные алгоритмом, либо закрашены (если этот ребра деревьев), либо помечены пунктиром (в противном случае). Ребра, не являющиеся ребрами деревьев, помечены на рисунке буквами В (обратные -back), F (прямые - forward) и С (перекрестные - cross). В вершинах указаны метки времени в формате открытие/завершение.
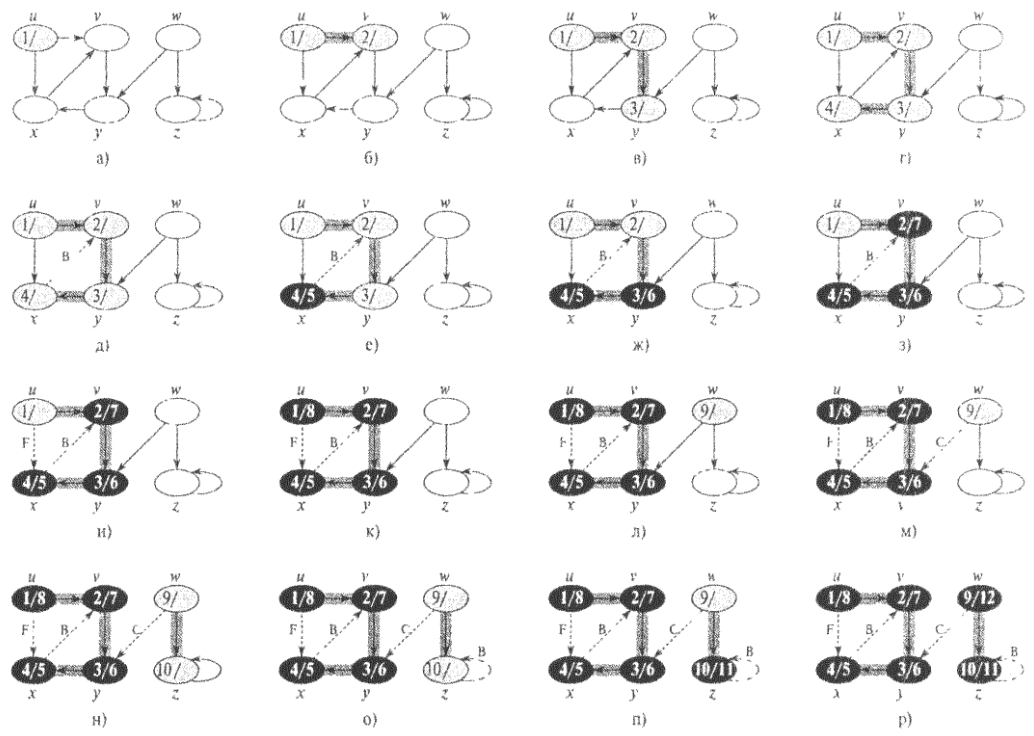
Рис. 24. Выполнение алгоритма поиска в глубину DFS над ориентированным графом
Процедура DFS работает следующим образом. В строках 1-3 все вершины окрашиваются в белый цвет, а их поля Prev инициализируются значением NULL. В строке 4 выполняется сброс глобального счетчика времени. В строках 5-7 поочередно проверяются все вершины из V, и когда обнаруживается белая вершина, она обрабатывается при помощи процедуры DFS_Visit. Каждый раз при вызове процедуры DFS_Visit(u) в строке 7, вершина и становится корнем нового дерева леса поиска в глубину. При возврате из процедуры DFS каждой вершине и сопоставляются два момента времени — время открытия (discovery time) u->d и время завершения (finishing time) u->f.
При каждом вызове DFS_Visit(u) вершина и изначально имеет белый цвет. В строке 1 она окрашивается в серый цвет, в строке 2 увеличивается глобальная переменная time, а в строке 3 выполняется запись нового значения переменной time в поле времени открытия u->d. В строках 4-7 исследуются все вершины, смежные с u, и выполняется рекурсивное посещение белых вершин. При рассмотрении в строке 4 вершины v Є get_adj(u), мы говорим, что ребро (и, v) исследуется (explored) поиском в глубину. И наконец, после того как будут исследованы все ребра, покидающие u, в строках 8-9 вершина и окрашивается в черный цвет, а в поле u->f записывается время завершения работы с ней.
Заметим, что результат поиска в глубину может зависеть от порядка, в котором выполняется рассмотрение вершин в строке 5 процедуры DFS, а также от порядка посещения смежных вершин в строке 4 процедуры DFS_Visit. На практике это обычно не вызывает каких-либо проблем, так как обычно эффективно использован может быть любой результат поиска в глубину, приводя по сути к одинаковым результатам работы алгоритма, опирающегося на поиск в глубину.
Чему равно время работы процедуры DFS? Циклы в строках 1-3 и 5-7 процедуры DFS выполняются за время Θ(V), исключая время, необходимое для вызова процедуры DFS_Visit. Процедура DFS_Visit вызывается ровно по одному разу для каждой вершины v Є V, так как она вызывается только для белых вершин, и первое, что она делает, — это окрашивает переданную в качестве параметра вершину в серый цвет. В процессе выполнения DFS_Visit(v) цикл в строках 4-7 выполняется get_adj(v) раз. Поскольку:
Σget_adj(v) = Θ(V),
общая стоимость выполнения строк 4-7 процедуры DFS_Visit равна Θ(Е). Время работы процедуры DFS, таким образом, равно Θ(V + Е).
Алгоритм Беллмана-Форда
Алгоритм Беллмана-Форда (Bellman-Ford algorithm) позволяет решить задачу о кратчайшем пути из одной вершины в общем случае, когда вес каждого из ребер может быть отрицательным. Для заданного взвешенного ориентированного графа G = (V, Е) с истоком s и весовой функцией w : Е -> R алгоритм Беллмана-Форда возвращает логическое значение, указывающее на то, содержится ли в графе цикл с отрицательным весом, достижимый из истока. Если такой цикл существует, в алгоритме указывается, что решения не существует. Если же таких циклов нет, алгоритм выдает кратчайшие пути и их вес.
В этом алгоритме используется ослабление, в результате которого величина v->d, представляющая собой оценку веса кратчайшего пути из истока s к каждой из вершин v Є V, уменьшается до тех пор, пока она не станет равна фактическому весу кратчайшего пути δ(s, v). Значение TRUE возвращается алгоритмом тогда и только тогда, когда граф не содержит циклов с отрицательным весом, достижимых из истока.
BELMAN_FORD(graph *G, vfunc *w, vertex *s){
1 initialize_single_source(g,s);
2 for(i = 1; i < vertex_count(G); i++){
edge *e = NULL;
3 while((e = get_edges(G,e)) != NULL){
4 relax(e->u, e->v, w);
}
}
e = NULL;
5 while((e = get_edges(G,e)) != NULL){
6 if(e->v->d > (e->u->d + w(e->u, e->v))
7 return false;
}
8 return true;
}
На рис. 25 проиллюстрирована работа алгоритма Bellman_Ford с графом, содержащим 5 вершин, в котором исток находится в вершине s.

Рис. 25. Выполнение алгоритма Беллмана-Форда
Рассмотрим, как работает алгоритм. После инициализации в строке 1 всех значений d и prev, алгоритм осуществляет |V| - 1 проходов по ребрам графа. Каждый проход соответствует одной итерации цикла for в строках 2-4 и состоит из однократного ослабления каждого ребра графа. После |V| - 1 проходов в строках 5-8 проверяется наличие цикла с отрицательным весом и возвращается соответствующее булево значение. В примере, приведенном на рис. 25, алгоритм Беллмана-Форда возвращает значение true.
На рис. 25 в вершинах графа показаны значения атрибутов d на каждом этапе работы алгоритма, а выделенные ребра указывают на значения предшественников: если ребро (u, v) выделено, то v->prev = u. В рассматриваемом примере при каждом проходе ребра ослабляются в следующем порядке: (t, х), (t, у), (t, z), (x, t), (y, х), (у, z), (z, x), (z, s), (s, t), (s, у). В части а рисунка показана ситуация, сложившаяся непосредственно перед первым проходом по ребрам. В частях б-д проиллюстрирована ситуация после каждого очередного прохода по ребрам. Значения атрибутов d и prev, приведенные в части д, являются окончательными.
Алгоритм Беллмана-Форда завершает свою работу в течение времени O(V E), поскольку инициализация в строке 1 занимает время Θ(V), на каждый из |V| - 1 проходов по ребрам в строках 2-4 требуется время Θ(E), а на выполнение цикла for в строках 5-7 — время О(Е).
Алгоритм Дейкстры
Алгоритм Дейкстры решает задачу о кратчайшем пути из одной вершины во взвешенном ориентированном графе G = (V, Е) в том случае, когда веса ребер неотрицательны. Поэтому в настоящем разделе предполагается, что для всех ребер (u, v) Є Е выполняется неравенство w (u, v) ≥ 0. Через некоторое время станет понятно, что при хорошей реализации алгоритм Дейкстры производительнее, чем алгоритм Беллмана-Форда.
В алгоритме Дейкстры поддерживается множество вершин S, для которых уже вычислены окончательные веса кратчайших путей к ним из истока s. В этом алгоритме поочередно выбирается вершина u Є V - S, которой на данном этапе соответствует минимальная оценка кратчайшего пути. После добавления этой вершины и в множество S производится ослабление всех исходящих из нее ребер.
В приведенной ниже реализации используется неубывающая очередь с приоритетами Q, состоящая из вершин, в роли ключей для которых выступают значения d.
DUKSTRA(graph *G, wfunc *W, vertex *S){
1 initialize_single_source(G,s);
2 S = init_set();
3 Q = init_p_queue();
4 while (!queue_empty(Q)){
5 vertex *u = extract_min(Q);
6 add_set(S,u);
vertex *v = NULL;
7 while((v = get_next_vertex(u,v)) != NULL)
8 relax(u,v,w);
}
}
}
Процесс ослабления ребер в алгоритме Дейкстры проиллюстрирован на рис. 26. Исток s расположен на рисунке слева от остальных вершин. В каждой вершине приведена оценка кратчайшего пути к ней, а выделенные ребра указывают предшественников. Черным цветом обозначены вершины, добавленные в множество S, а белым - содержащиеся в неубывающей очереди с приоритетами Q = V - S. В части а рисунка проиллюстрирована ситуация, сложившаяся непосредственно перед выполнением первой итерации цикла while в строках 4-8. Выделенная серым цветом вершина имеет минимальное значение d и выбирается в строка S в качестве вершины и для следующей итерации. В частях б-е изображены ситуации после выполнения очередной итерации цикла while. В каждой из этих частей выделенная серым цветом вершина выбирается в качестве вершины u в строке 5. В части е приведены конечные значения величин d и prev.
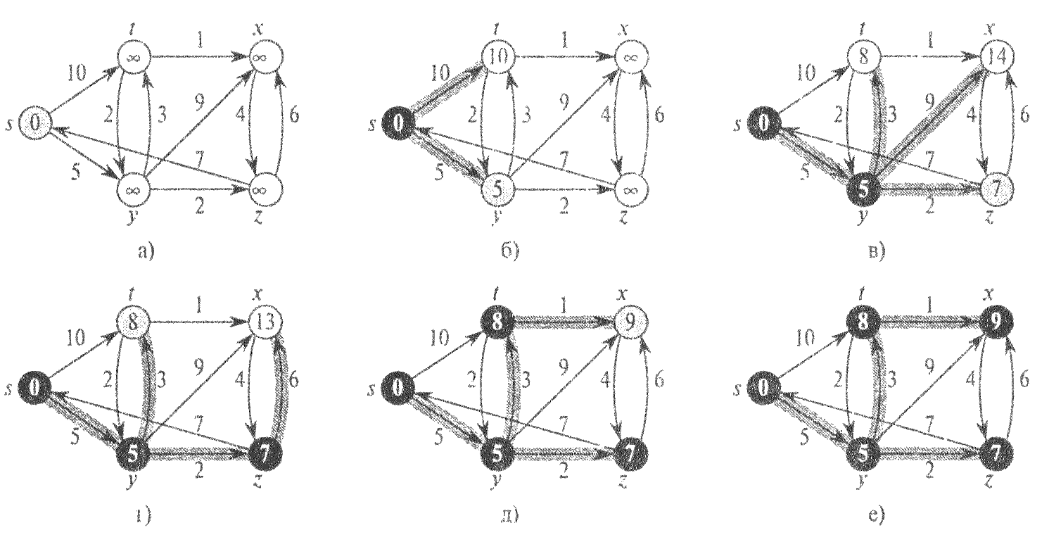
Рис. 26. Выполнение алгоритма Дейкстры
Опишем работу рассматриваемого алгоритма. В строке 1 производится обычная инициализация величин d и prev, а в строке 2 инициализируется пустое множество вершин S. В этом алгоритме поддерживается инвариант, согласно которому в начале каждой итерации цикла while в строках 4-8 выполняется равенство Q = V — S. В строке 3 неубывающая очередь с приоритетами Q инициализируется таким образом, чтобы она содержала все вершины множества V; поскольку в этот момент S = 0, после выполнения строки 3 сформулированный выше инвариант выполняется. При каждой итерации цикла while в строках 4-8 вершина u извлекается из множества Q = V — S и добавляется в множество S, в результате чего инвариант продолжает соблюдаться. (Во время первой итерации этого цикла u = s.) Таким образом, вершина u имеет минимальную оценку кратчайшего пути среди всех вершин множества V — S. Затем в строках 7-8 ослабляются все ребра (u, v), исходящие из вершины u. Если текущий кратчайший путь к вершине v может быть улучшен в результате прохождения через вершину u, выполняется ослабление и соответствующее обновление оценки величины v->d и предшественника v->prev. Обратите внимание, что после выполнения строки 3 вершины никогда не добавляются в множество Q и что каждая вершина извлекается из этого множества и добавляется в множество S ровно по одному разу, поэтому количество итераций цикла while в строках 4-8 равно | V|.
Поскольку в алгоритме Дейкстры из множества V — S для помещения в множество S всегда выбирается самая «легкая» или «близкая» вершина, говорят, что этот алгоритм придерживается “жадной стратегии”. “Жадные стратегии” не всегда приводят к оптимальным результатам, однако, алгоритм Дейкстры действительно находит кратчайшие пути.
Порядок выполнения работы
1. Ознакомиться с теоретическими сведениями.
2. Получить вариант задания у преподавателя.
3. Выполнить задание.
4. Продемонстрировать выполнение работы преподавателю.
5. Оформить отчет.
6. Защитить лабораторную работу.
Дата добавления: 2019-09-13; просмотров: 238; Мы поможем в написании вашей работы! |

Мы поможем в написании ваших работ!
