Линейные неоднородные уравнения высшего порядка.
Томский государственный университет систем управления и радиоэлектроники
Приходовский М.А.
Математика
Курс практических занятий
Семестр 3
Учебное пособие для специальности
Прикладная информатика в экономике»
Томск
ТУСУР
2019
Электронное учебное пособие составлено по материалам практических занятий на ФСУ в группах 448-1,2 осенью 2019 года.
Оглавление
| Линейные дифференциальные уравнения высшего порядка Циркуляция, формула Грина Потенциальные векторные поля | 5 15 18 |
Содержание по номерам задач и датам практик
| 448-1 | задачи: | 448-2 | ||
| Практика 1 | 2.9 | 1-10 | 7.9 | 1-10 |
| Практика 2 | 4.9 | 11-17 | ||
Линейные дифференциальные уравнения высшего порядка.
Необходимо рассмотреть несколько теоретических моментов.
Теорема 1. Функция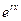 
является решением линейного однородного дифференциального уравнения 
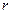есть характеристический корень.
Доказательство. Ищем решение в виде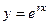 
.
Если 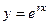, то 
, 
, ... 
.
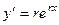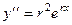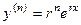Подставим в уравнение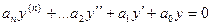 
.
Получим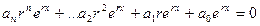 
.
Во всех слагаемых одинаковая экспонента, вынесем её за скобку:
|
|
|
.
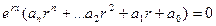Но поскольку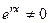 
, то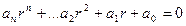 
.
Что и требовалось доказать.
Теорема 2. Линейная комбинация решений линейного однородного дифференциального уравнения тоже является его решением.
Доказательство. (ДОК 23)
Пусть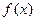 
и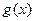 
- два различных решения уравнения
.
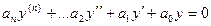То есть, они оба обращают его в тождество:
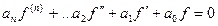и
.
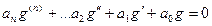Надо доказать, что линейная комбинация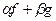 
тоже подходит в качестве решения. Известно, что для производной, а также и последующих выполняется свойство линейности: 
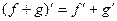, поэтому 
, 
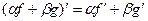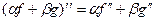, и т.д.
Тогда, подставляя линейную комбинацию в дифференциальное уравнение, получим:
=
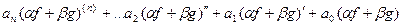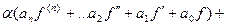
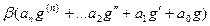
Но ведь в каждой скобке 0, так как каждая из этих функция была решением уравнения. Получается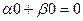 
.
Таким образом, линейная комбинация решений тоже является решением линейного уравнения.
Задача 1. Решить уравнение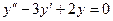 
.
Решение. Характеристическое уравнение: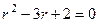 
, оно сводится к виду 
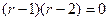, корни 
, 
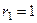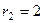. Тогда решениями могут быть только 
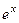и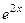 
. Сделаем проверку для каждой из экспонент. Подставим каждую из них в уравнение.
1) 
= 
.
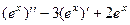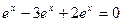2) 
= 
.
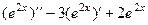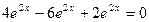Проверка выполнена. Обе экспоненты являются решениями.
При этом никакая третья экспонента не может служить решением этого же уравнения, потому что характеристический многочлен 2-й степени, и он имеет максимум 2 корня.
|
|
|
Их линейная комбинация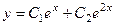 
.
Ответ. .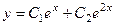
Задача 2. Найти общее решение дифф. уравнения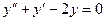 
.
Решение. Характеристическое уравнение: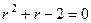 
, его корни
1 и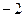 
. Тогда ФСР = 
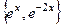, и общее решение: 
.
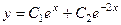Ответ. .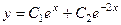
Задача 3. Найти частное решение дифф. уравнения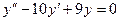 
при условиях Коши: 
.
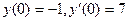Решение. Характеристическое уравнение: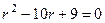 
, его корни: , 
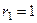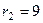. Тогда ФСР состоит из 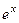и 
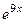, общее решение такое: 
.
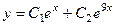Теперь найдём решение задачи Коши. Сначала запишем функцию и её производную: 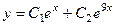и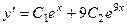 
.
Кроме того, у нас есть информация: .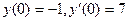
Тогда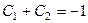 
, 
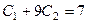. Получается система уравнений
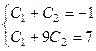вычитая 1-е уравнение из 2-го, находим, 
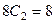, т.е. 
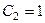, тогда 
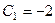. Тогда частное решение: 
.
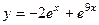Ответ. Общее решение 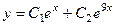, частное .
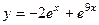Задача 4. Решить уравнение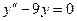 
, найти частное решения для условий Коши: 
.
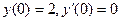Решение. Характеристическое уравнение: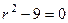 
, его корни: 
, 
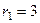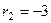. Тогда ФСР состоит из 
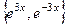, общее решение такое: 
.
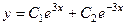Теперь найдём решение задачи Коши. Сначала запишем функцию и её производную:
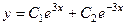и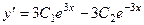 
.
Кроме того, у нас есть информация: .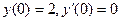
Ищем частное решение.
, 
, 
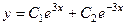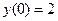
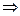
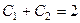
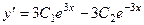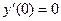
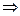
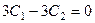
Получается система уравнений
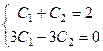, решая её, находим из 2-го 
,
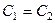откуда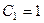 
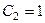, . Тогда частное решение: 
.
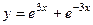Ответ. .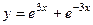
Если 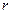- корень кратности 
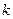, то в системе решений будут присутствовать 
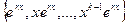, то есть одну и ту же экспоненту 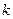раз включать в фундаменатльную систему решений нельзя, иначе фактическое количество функций в ФСР получится меньше, чем n.
|
|
|
Кроме самой экспоненты, нужно взять ещё и с домножением на степенные, по нарастанию степеней до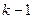 
.
Задача 5. Решить уравнение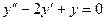 
.
Решение. Характеристическое уравнение: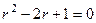 
, то есть 
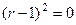, характеристическое корни 
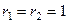. Тогда ФСР: 
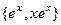, а общее решение: 
.
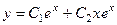Ответ. .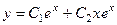
Сделаем проверку. Для 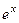очевидно. Проверим 
.
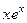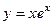, тогда 
, 
.
= 
= 
= 
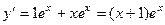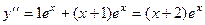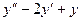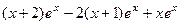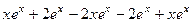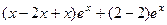= 0.
Если один из корней 0, то в ФСР присутствует экспонента вида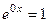 
, то есть контанта 1 принадлежит ФСР.
Задача 6. Решить уравнение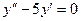 
.
Решение. Характеристическое уравнение: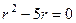 
, корни 0 и 5. Тогда ФСР: 
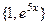, а общее решение: 
.
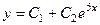Ответ. .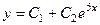
***
Ещё одно небольшое теоретическое отступление. Докажем, что если 0 является корнем кратности 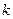, то система решений, соответствующих этому корню, имеет вид 
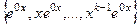, то есть 
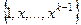. Характеристическое уравнение обязательно имеет вид 
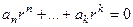, так как 
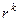можно вынести за скобку 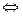0 корень кратности 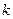. Но это значит, что исходное дифференциальное уравнение имеет вид 
.
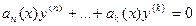Оно содержит производные порядка 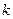и выше. Известно, что если степенную функцию продифференцировать столько раз, какова её степень, то получим константу, а если большее количество раз, то обратится в 0. Так, например,
|
|
|
, 
.
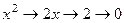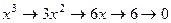В данном уравнении производные порядка 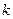и выше. Любая из степенных функций порядка 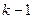и ниже, а именно взятая из набора 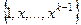, является решением.
Случай комплексных корней. Если присутствуют два сопряжённых корня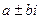 
то общее решение: 
.
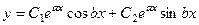Задача 7. Найти общее решение уравнения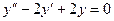 
.
Решение. Характеристическое уравнение: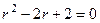 
.
Ищем его корни.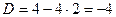 
. Корни 
= 
=
= 
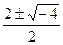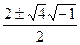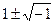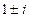. Найдём действительную и мнимую части функции 
= 
= 
= 
.
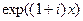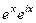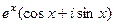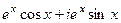Две линейно-независимых функции образуют ФСР:
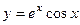и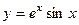 
. Общее решение: 
.
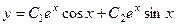Ответ.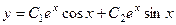 
.
Проверка. Проверим, например, одно из слагаемых.
= 
.
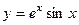
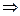
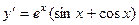
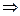
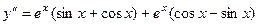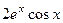Подставим в уравнение.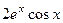 
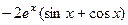
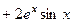= 0.
Задача 8. Найти общее решение уравнения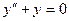 
.
Решение. Характеристическое уравнение: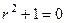 
, т.е. 
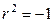корни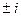 
, то есть 
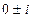. Две линейно-независимых функции образуют ФСР: 
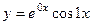и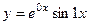 
.
Общее решение: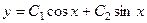 
.
Ответ. .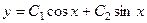
Линейные неоднородные уравнения высшего порядка.
Дата добавления: 2019-09-13; просмотров: 119; Мы поможем в написании вашей работы! |
Мы поможем в написании ваших работ!