Пример расчета и построения характеристик и диаграмм

⇐ ПредыдущаяСтр 16 из 17Следующая ⇒

Синхронного генератора

Исходные данные для расчета:

номинальная мощность, Р_Н = 100 МВт;

номинальное напряжение, U_H = 15,75 кВ;

коэффициент мощности cosφ_H = 0,707;

отношение короткого замыкания ОКЗ = 1,5;

индуктивное сопротивление рассеяния якоря, x_σa = 0,2;

схема соединения обмоток статора – звезда.

1. Построение характеристики ХХ Е₀ = f(I _В).

При расчетах параметров СГ можно исходить из нормальной характеристики ХХ, полученной как средняя на основании большого количества испытаний машин. Эта характеристика, выраженная в о.е., представлена в табл. 4.1. Характеристика ХХ, построенная по данным этой таблицы представлена на рис. 4.1.

Таблица 4.1

Нормальная характеристика ХХ

I _В	0	0,25	0,5	0,75	1,0	1,25	1,5	1,75	2	2,5
Е₀	0	0,29	0,56	0,82	1,0	1,15	1,23	1,27	1,31	1,33

2. Построение характеристики КЗ I _К = f(I _В).

Так как характеристика КЗ прямолинейна, то построим её по двум точкам: 1) точка начала координат 0; 2) точка М, соответствующая единичной величине тока возбуждения и ОКЗ.

Для построения характеристика КЗ по величине ОКЗ при единичной величине тока возбуждения, находим I _ВК – ток возбуждения, соответствующий по характеристике КЗ номинальному току якоря I _К= I _Н:

так как , то 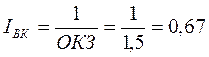. На рис. 4.1 характеристика КЗ представлена прямой ОМ.

Рис. 4.1 Характеристики ХХ и КЗ и треугольник КЗ синхронного генератора

3. Построение треугольника КЗ.

На рис. 4.1 точку М для тока I _К= I _Н = 1 сносим на ось абсцисс – получаем точку А. ЭДС рассеяния, выраженную в о.е.: Е _σa = I_H · x_σa = 1· 0,2 = 0,2, откладываем на оси ординат и сносим на характеристику ХХ – получаем точку В. Из точки В опускаем перпендикуляр на ось абсцисс – получаем точку С. ΔСВА – треугольник КЗ.

4. Определение МДС реакции якоря при номинальном режиме

МДС реакции якоря в масштабе тока возбуждения определяется отрезком [СА] на рис. 4.1.

5. Вычисление синхронных реактивных сопротивлений x_d и x_q .

Продолжая перпендикуляр на рис. 4.1 от точки А до пересечения с характеристикой ХХ – получим т. N. Отрезок [А N] соответствует ЭДС . По этой ЭДС определяем синхронное реактивное сопротивление по продольной оси . Синхронное реактивное сопротивление по поперечной оси можно принять равным x_q = 0,64· x_d = 0,64 · 0,73 = 0,47.

6. Построение диаграммы МДС (диаграммы Потье)

Активным сопротивлением обмотки статора, ввиду его малости, пренебрегаем. На рис. 4.2 строим такую же характеристику ХХ, как на рис. 4.1. На этом же рисунке совместим вектор U_H _Ф = 1с положительным направлением оси ординат. Проводим вектор тока I _Н под углом φ_H = arcos(φ_H)= arccos (0,707) = 45⁰ к вектору напряжения U_H _Ф. Под углом 90⁰ к току I _Н проводим прямую через конец вектора напряжения U_H _Ф. По этой линии от конца вектора U_H _Ф откладываем вектор ЭДС рассеяния обмотки якоря Е _σa = 0,2– получаем точку В.

Соединяя точку В с точкой начала координат 0 – получаем вектор индуктируемой в генераторе ЭДС Е_δ. Поворачивая этот вектор до совмещения его с осью ординат – получаем точку В'. Сносим точку В' на характеристику ХХ в точку В'' . Из точки В'' опускаем перпендикуляр на ось абсцисс до точки А. Отрезок [ОА] является величиной тока возбуждения Е _B_δ, необходимого для создания ЭДС Е_δ.

Для учета РЯ воспользуемся диаграммой рис.4.1. Отрезок [СА] является МДС реакции якоря в масштабе тока возбуждения I _Ва = 0,48. Для получения полного тока возбуждения I _В0 сложим геометрически векторы I _В _δ и I _Ва, где угол φ' = φ_Н + θ = 45⁰ + 7⁰ = 52⁰ (угол θ – это угол нагрузки – угол сдвига между напряжением на зажимах машины U_H и ЭДС, индуктируемой в генераторе Е_δ). Описав дугу радиусом ОС до пересечения с осью абсцисс в точке D, получим ток возбуждения I _В0 = [О D]. При сбросе нагрузки этот ток возбуждения создаст ЭДС Е₀ = [D Н].

Рис.4.2 Диаграмма МДС (диаграмма Потье) для номинального режима

Синхронного генератора

Для нахождения угла ψ_Н – угла между током нагрузки I _Н и индуктируемой ЭДС Е₀, делаем дополнительные построения. Точку Н с характеристики ХХ сносим на ось ординат – получаем точку Н'. Поворачиваем вектор Е₀ = [ОН'] вокруг точки 0 под углом 90⁰ к вектору I _В0 = [ОС]. Угол между ЭДС Е₀ и током I _Н есть искомый угол ψ_Н = 56⁰.

7. Построение диаграммы ЭДС (диаграммы Блонделя)

Для построения диаграммы ЭДС нужно определить продольную и поперечную составляющие тока I _Н по ортогональным осям d и q (ось d направлена вдоль оси полюсов явно выраженного ротора, а ось q – поперёк):

I_d = I _Н ·sin ψ_Н = 1·sin(56⁰)= 0,829 ;

I_q = I _Н ·cos ψ_Н = 1·cos(56⁰)= 0,559.

Составляющие полной ЭДС реакции якоря Е_а по продольной и поперечной осям:

Е _d = I_d · х _d = 0,829·0,73= 0,605;

Е _q = I_q · х _q = 0,559·0,47= 0,263.

Силовые линии магнитного поля возбуждения (Ф_В) и МДС обмотки возбуждения (F _В) направлены вдоль оси d. А индуктируемая этим полем ЭДС Е₀ отстает от этого поля (и от оси d) на 90⁰, следовательно, индуктируемая ЭДС Е₀направлена по оси q.

По найденным величинам строим диаграмму ЭДС (рис. 4.3). При построении учитывать, что вектор Е _d опережает на 90⁰ вектор тока I_d, а вектор Е _q – на 90⁰ вектор тока I_q.

Рис. 4.3 Диаграмма ЭДС (диаграмма Блонделя) для номинального режима

Синхронного генератора

8. Построение диаграммы МДС для различных нагрузок

Задаемся различными реактивными токами I _р = 0; 0,5; 0,75; и 1 А при постоянной активной составляющей I _а = 0,5 А. По активной и реактивной составляющим тока определяем полный ток:

Коэффициент мощности и соответствующие углы равны:

нагрузка чисто активная φ₀ = 0;

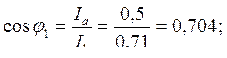φ₁ = arcos (0,704) = 45⁰;

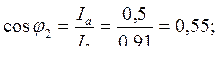φ₂ = arcos (0,55) = 57⁰;

φ₃ = arcos (0,45) = 63⁰.

Зная эти величины, строим диаграмму МДС (рис. 4.4). Диаграмма строится в о.е. При чисто активной нагрузке (I _а = 0,5) полный ток I ₀ совпадает с вектором напряжения U _НФ и равен I₀= I _а = 0,5. Т.к. I _а = const, то концы векторов полного тока опираются на прямую, проходящую параллельно оси абсцисс через точку С.Под углами φ₁, φ₂, φ₃ проводим прямые для отстающего тока (вектор результирующего тока отстаёт от напряжения). Для опережающего тока произвольно задаёмся двумя значениями углов φ₄= –30⁰ и φ₅= –45⁰ и проводим линии. На этих линиях из начала координат до пересечения с прямой, проведенной через точку С , откладываем вектора полных токов I₁, I₂, I₃, I₄, I₅. Значение токов I₄ и I₅вычисляем по заданным углам:

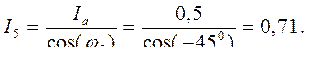
Рис. 4.4 Диаграмма МДС синхронного генератора для различных нагрузок

Находим значения ЭДС рассеяния для каждого тока нагрузки:

Вектора, соответствующие этим ЭДС, откладываем от конца вектора напряжения U _НФ (точки В) под прямым углом к векторам соответствующих полных токов.

Частичные значения МДС реакции якоря в масштабе тока возбуждения находим по формуле , где I _Ва = 0,48 получено графически из рис. 4.1. В результате расчета для различных полных токов частичные значения МДС реакции якоря в масштабе тока возбуждения равны:

Далее, концы векторов поворачиваем вокруг точки В до пересечения с осью ординат. Точки, полученные на оси ординат, сносим на характеристику ХХ и из них опускаем перпендикуляры до пересечения с осью абсцисс. Из этих полученных точек под углом φ' = φ + θ откладываем в масштабе тока возбуждения частичные значения МДС реакции якоря. Замыкающий вектор даст необходимый ток возбуждения при определённой нагрузке:

φ₀' = φ₀ + θ = 0 + 7⁰ = 7⁰; I _В₀ = 1,2;

φ₁' = φ₁ + θ = 45⁰ + 7⁰ = 52⁰; I _В₁ = 1,52;

φ₂' = φ₂ + θ = 57⁰ + 7⁰ = 64⁰; I _В₂ = 1,76;

φ₃' = φ₃ + θ = 63⁰ + 7⁰ = 70⁰; I _В₃ = 2;

φ₄' = φ₄ + θ = –30⁰ + 7⁰ = –23⁰; I _В₄ = 0,78;

φ₅' = φ₅ + θ = –45⁰ + 7⁰ = –38⁰; I _В₅ = 0,64.

На диаграмме МДС (рис. 4.4) углы (φ₃, φ₃') и векторы (Е_σ₃, I _Ва₃, I _В₃) показаны только для режима № 3.

9. Построение U –образной характеристики генератора.

9.1. при активном токе статора I_a = 0,5

По рассчитанным токам нагрузки (п.8) и соответствующим токам возбуждения, полученным в результате построения (рис. 4.4), составим таблицу 4.2 для построения U–образной характеристики при I_a = 0,5. Соответствующая характеристика построена на рис. 4.5.

Таблица 4.2

Данные для построения U –образной характеристики для I_a = 0,5

Порядковый номер режима	5	4	0	1	2	3
I, A	0,71	0,57	0,5	0,71	0,91	1,12
I_B, A	0,64	0,78	1,2	1,52	1,76	2

Рис. 4.5 U –образные характеристики синхронного генератора

9.2 при активном токе статора I_a = 0.

Мощность является чисто реактивной (cosφ = 0, φ = 90⁰) поэтому реактивные токи нагрузки I _р и соответствующие токи возбуждения I_B ₀, I_B ₁, I_B ₂, I_B ₃, I_B ₄, I_B ₅ откладываются по оси абсцисс (рис. 4.6). При отстающем токе нагрузки (I_B ₁, I_B ₂, I_B ₃) соответствующие составляющие (I _В _δ и I _Ва) складываются, а при опережающем (I_B ₄, I_B ₅) – составляющие I _В _δ и I _Ва вычитаются. ЭДС рассеяния Е _σa при отстающем токе откладывается вверх от точки В, а при опережающем – вниз.

Для построения диаграммы МДС при I_a = 0реактивные токи для отстающих токов нагрузки примем те же: I _р = 0; 0,5; 0,75, а для опережающих: I _р = 0,5 и 0,75. Так как I_a = 0, то полные токи равны реактивным. Находим значения ЭДС рассеяния для каждого тока нагрузки:

I₀= 0;

I₁= 0,5;

I₂= 0,75;

I₃= 1;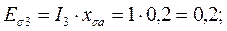

I₄= 0,5;

I₅= 0,75;

Частичные значения МДС реакции якоря в масштабе тока возбуждения для тех же токов нагрузки равны:

Рис. 4.6 Диаграмма МДС синхронного генератора при I_a =0

По токам нагрузки и соответствующим токам возбуждения, полученным в результате построения (рис. 4.6), составим таблицу 4.3 для построения U–образной характеристики при I_a = 0. Соответствующая характеристика также построена на рис. 4.5.

Таблица 4.3

Данные для построения U –образной характеристики для I_a = 0

Порядковый номер режима	5	4	0	1	2	3
I, A	0,75	0,5	0	0,5	0,75	1
I_B, A	0,4	0,6	1,0	1,4	1,6	1,9

Дата добавления: 2019-09-13; просмотров: 1408; Мы поможем в написании вашей работы!

Поделиться с друзьями:

⇐ Предыдущая 8 9 10 11 12 13 14 151617 Следующая ⇒

Мы поможем в написании ваших работ!