Пример получения определяющих соотношений для случая малых деформаций.
Лемма Фурье

| (10) |
Из (2) и (3) следует Фундаментальная теорема Фурье-Стокса:
Если  - непрерывная функция по
- непрерывная функция по  , удовлетворяющая (10), то существует такое векторное поле теплового потока
, удовлетворяющая (10), то существует такое векторное поле теплового потока  , что
, что

| (11) |
Минус перед вектором  берется для того, чтобы подчеркнуть, что мы описываем именно приток тепла – то есть вектор направлен навстречу вектору внешней нормали
берется для того, чтобы подчеркнуть, что мы описываем именно приток тепла – то есть вектор направлен навстречу вектору внешней нормали  .
.
Пользуясь формулой Гаусса-Остроградского мы можем выразить скорость подвода тепла в виде единого интеграла по объему

| (12) |
Первый закон термодинамики
Скорость изменения полной энергии системы равна сумме мощности работы внешних сил и скорости притока тепла извне
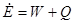
| (13) |
Полная энергия системы представляется в виде суммы кинетической энергии и внутренней энергии.
 , ,  , , 
| (14) |
Из (14) получаем с учетом уравнения неразрывности

| (15) |
Из (5), (12), (13) и (15) получаем уравнение энергии

| (16) |
В силу произвольности объема получаем дифференциальное уравнение энергии для точки среды

| (17) |
Но с учетом уравнения движения, слагаемые при сомножителе – компоненте скорости сокращаются

| (18) |
Мы получили уравнение притока тепла (уравнение баланса энергии) в простом виде для точки среды:

| (19) |
Для некоторого объема среды мы получим его , проинтегрировав (19) по объему

| (20) |
где  - мощность работы внутренних поверхностных сил.
- мощность работы внутренних поверхностных сил.
|
|
|
Второй закон термодинамики
Один из видов формулировка второго закона термодинамики состоит из четырех утверждений для новой функции состояния системы  , называемой энтропией:
, называемой энтропией:
 , при этом , при этом 
| (21) |
 если процесс обратимый
если процесс обратимый
 - приток энтропии извне определяется либо притоком массы, либо притоком тепла.
- приток энтропии извне определяется либо притоком массы, либо притоком тепла.
 , если нет притока массы к системе и во всех ее точках температура одинакова. , если нет притока массы к системе и во всех ее точках температура одинакова.
| (22) |
То есть на основании равенств (21)и (22) и неравенства из (21) мы имеем важное неравенство

| (23) |
Выражая скорость притока тепла  из (19) в виде
из (19) в виде  , получаем из (23)
, получаем из (23)
Неравенство Клаузиуса-Дюгема.

| (24) |
Или, переходя к подынтегральным выражениям, вводя плотность энтропии  как
как 

| (25) |
Итак, на данный момент мы имеем следующие уравнения, которые выполняются для любой сплошной среды, некоего термомеханического континуума.
 уравнение неразрывности уравнение неразрывности
| (26) |
 уравнение движения уравнение движения
| (27) |
 уравнение притока тепла (ур-е энергии) уравнение притока тепла (ур-е энергии)
| (28) |
 неравенство Клаузиуса-Дюгема неравенство Клаузиуса-Дюгема
| (29) |
Мы имеем пять независимых уравнений, одно неравенство и… шестнадцать неизвестных!
|
|
|
Плотность, три компоненты вектора скорости, шесть компонент тензора напряжений, три компоненты вектора потока тепла, плотность внутренней энергии, температура и плотность энтропии.
Где взять еще одиннадцать уравнений?
Шесть дают определяющие соотношения, связывающие в единую энергетическую пару некий тензор деформации 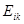 и соответствующий ему тензор напряжений
и соответствующий ему тензор напряжений  , так, что плотность мощности работы внутренних сил представима в виде свертки одного тензора на полную производную по времени от второго
, так, что плотность мощности работы внутренних сил представима в виде свертки одного тензора на полную производную по времени от второго  . При условии введения параметров состояния для плотности внутренней энергии в виде пары – энтропия и тензор деформаций, мы получаем следующее определяющее соотношение
. При условии введения параметров состояния для плотности внутренней энергии в виде пары – энтропия и тензор деформаций, мы получаем следующее определяющее соотношение

| (30) |
Одно уравнение дает связь плотности энтропии, внутренней энергии и температуры

| (31) |
Вводя температуру  как еще одну степень свободы наравне с деформацией, мы можем, согласно закону Фурье для изотропного тела, выразить вектор потока тепла через температуру:
как еще одну степень свободы наравне с деформацией, мы можем, согласно закону Фурье для изотропного тела, выразить вектор потока тепла через температуру:
 , где , где  - коэффициент теплопроводности. - коэффициент теплопроводности.
| (32) |
Это еще три уравнения. И последнее уравнение постулируется в виде калорического уравнения
|
|
|

| (34) |
Пример получения определяющих соотношений для случая малых деформаций.
В случае симметрии тензора напряжений
 , где , где  тензор скоростей деформаций тензор скоростей деформаций
| (35) |
В случае малых деформаций
 , где , где 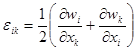 тензор малых деформаций, тензор малых деформаций,
| (36) |
Неравенство Клаузиуса-Дюгема для точки среды для малых деформаций:

| (37) |
Параметры состояния системы в случае использования плотности потенциала внутренней энергии берутся плотность энтропии и деформация, при этом

| (38) |
Удобно выбрать другой термодинамический потенциал – свободная энергия  (свободная энергия Гельмгольца).
(свободная энергия Гельмгольца).
 , где , где  – плотность свободной энергии – плотность свободной энергии
| (39) |
Для него параметрами состояния системы являются температура и деформация

| (40) |
Тогда неравенство (37) сводится к виду

| (41) |
Группируя множите при скоростях изменения параметров состояния

| (42) |
Получаем, что при условии произвольности знаков скорости изменения каждого из параметров состояния обязаны выполняться следующие равенства, являющиеся определяющими соотношениями для нашей среды в случае малых деформаций:
 при при 
| (43) |
Последнее соотношение в случае постулирования линейной зависимости напряжений от деформаций приводит к тензорно линейному соотношению, которое в случае дополнительных предположений об однородности и изотропии материала приводит к известному закону Гука для линейного однородного изотропного упругого тела:
|
|
|
 при при 
| (44) |
Дата добавления: 2019-09-13; просмотров: 62; Мы поможем в написании вашей работы! |

Мы поможем в написании ваших работ!
