Лекция 2. Матрицы. Виды матриц. Алгебра матриц. Обратная матрица. Теорема существования, и единственности обратной матрицы.
Опр. : Матрицей размера 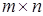 называется совокупность чисел или объектов другой природы, расположенных в виде прямоугольной таблицы в m строках и n столбцах:
называется совокупность чисел или объектов другой природы, расположенных в виде прямоугольной таблицы в m строках и n столбцах:
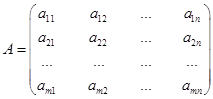 =
= 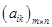 .
.
Первый индекс i элемента матрицы aikозначает номер строки, а второй индекс k – номер столбца, в которых стоит этот элемент.
Матрицей – столбцом называется матрица, у которой n = 1, т.е. число столбцов равно единице: 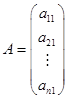 .
.
Матрицей – строкой называется матрица, у которой m = 1, т.е. число строк равно единице: 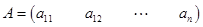 .
.
Квадратной матрицей называется матрица, у которой m = n, т.е. число строк равно числу столбцов, а число n называется порядком квадратной матрицы. Элементы 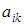 , где
, где 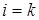 – образуют главную диагональ матрицы.
– образуют главную диагональ матрицы.
Диагональной матрицей называется квадратная матрица, все элементы которой вне главной диагонали равны нулю:
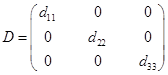 .
.
Единичной называется диагональная матрица, у которой все 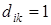 :
:
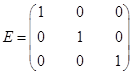
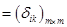 ,
,
где 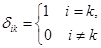 - символ Кронекера.
- символ Кронекера.
Нулевой называется матрица, у которой все элементы равны нулю:
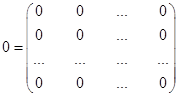 .
.
Транспонированной матрицей АТ называется матрица, которая получается из исходной путем замены строк столбцами:
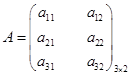
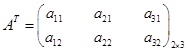 .
.
Симметрической называется матрица, для которой 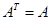 , т.е.
, т.е. 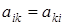 -
-
элементы, симметричные относительно главной диагонали, равны.
Кососимметрической называется матрица, для которой 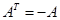 , т.е.
, т.е. 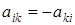 - элементы, симметричные относительно главной диагонали, отличаются только знаком. Очевидно, что у такой матрицы элементы главной диагонали равны нулю.
- элементы, симметричные относительно главной диагонали, отличаются только знаком. Очевидно, что у такой матрицы элементы главной диагонали равны нулю.
|
|
|
Равными считаются две матрицы одинакового размера, если равны их элементы, стоящие на одинаковых местах.
Операции над матрицами
Сложение матриц
Матрицы одинаковых размеров можно складывать, при этом получается матрица того же размера, что и слагаемые, а элементы ее образуются сложением элементов, стоящих на одинаковых местах:
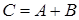 , где
, где 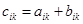 . (1)
. (1)
Свойства сложения матриц:
1). коммутативность: 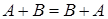 ;
;
2). ассоциативность: 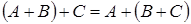 ;
;
3). 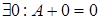 ;
;
4). 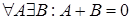 ,
, 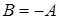 .
.
Умножение матриц на число
Любую матрицу можно умножить на число (скаляр), при этом получается матрица того же размера, а элементы ее получаются умножением на заданное число всех элементов данной матрицы:
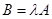 , где
, где 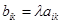 и
и 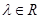 . (2)
. (2)
Свойства умножения матриц на число:
1). дистрибутивность относительно матричной суммы: 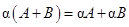 ;
;
2). дистрибутивность относительно скалярной суммы: 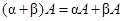 ;
;
3). ассоциативность относительно произведения скаляров: 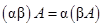 ;
;
4). существование элемента нейтрального относительно умножения на скаляр: 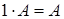 .
.
Умножение матриц
Произведением матрицы 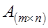 на матрицу
на матрицу 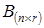 является матрица
является матрица 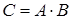 размера
размера 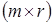 , элемент
, элемент 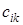 которой равен результату умножения i -ой строки матрицы А на k -ый столбец матрицы В
которой равен результату умножения i -ой строки матрицы А на k -ый столбец матрицы В
|
|
|
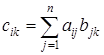 . (3)
. (3)
Перемножить можно только такие матрицы А и В, которые удовлетворяют правилу размеров:
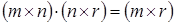 , (4)
, (4)
т.е. число столбцов матрицы А должно быть равно числу строк матрицы В.
В общем случае произведение матриц не коммутативно, т.е. 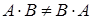 . Если же
. Если же 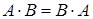 , то такие матрицы называются коммутирующими (перестановочными).
, то такие матрицы называются коммутирующими (перестановочными).
Свойства умножения матриц:
1). ассоциативность: 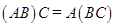 ;
;
2). дистрибутивность: 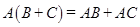 или
или 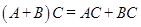 ;
;
3). ассоциативность относительно произведения на скаляр: 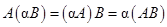 ;
;
4). 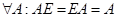 , где E - единичная матрица;
, где E - единичная матрица;
5). 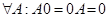 , где 0 – нулевая матрица.
, где 0 – нулевая матрица.
Задача 1
Найти матрицу C = 3A + 4B, если
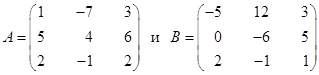 .
.
Решение
Используя свойства сложения и умножения матриц на число, получим
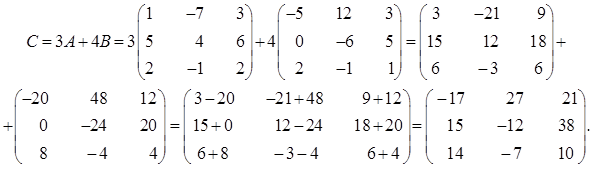
ОБРАТНАЯ МАТРИЦА
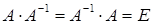 Матрица
Матрица 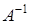 называется обратной матрице А, если , т.е. произведение этих матриц равно единичной матрице.
называется обратной матрице А, если , т.е. произведение этих матриц равно единичной матрице.
Для того чтобы матрица А имела обратную матрицу, необходимо и достаточно, чтобы она была невырожденной, т.е. чтобы 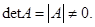
Алгоритм построения обратной матрицы.
1). Вычисляем 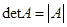 . Если
. Если 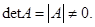 , то
, то 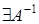 .
.
2). Транспонируем 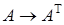 .
.
3). Строим присоединенную (союзную) матрицу 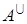 заменой
заменой 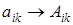 .
.
|
|
|
4). 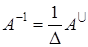 .
.
Свойства обратной матрицы:
1). 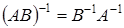 ;
;
2). 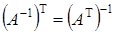 ;
;
3). 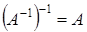 ;
;
4). 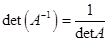 .
.
Задание 1
Найти матрицу, обратную матрице 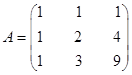 .
.
Решение
I способ
1. Вычислим определитель данной матрицы:
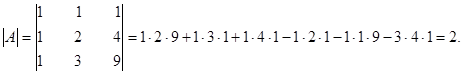
Так как определитель матрицы А отличен от нуля, т.е. 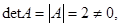 то данная матрица невырожденная и, следовательно, имеет обратную матрицу.
то данная матрица невырожденная и, следовательно, имеет обратную матрицу.
2. Транспонируем матрицу А:
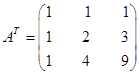 .
.
3. Найдем присоединенную матрицу 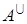 . Для этого вычислим алгебраические дополнения каждого элемента матрицы АТ:
. Для этого вычислим алгебраические дополнения каждого элемента матрицы АТ:
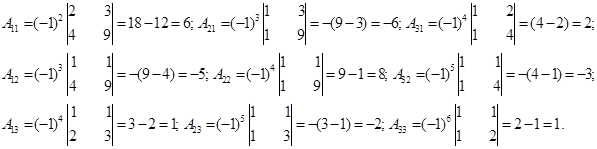
Присоединенная матрица 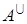 будет иметь вид
будет иметь вид
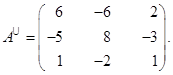
4. Так как 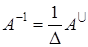 , то можно записать обратную матрицу:
, то можно записать обратную матрицу:
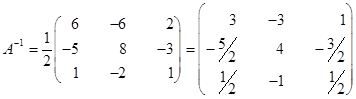 .
.
II способ
Обратную матрицу можно вычислить с помощью элементарных преобразований вспомогательной матрицы. Для этого необходимо следующее.
1. Составить вспомогательную матрицу, которая получается, если к исходной матрице приписать справа единичную матрицу того же размера.
2. Путем элементарных преобразований строк вспомогательной матрицы получить в левой ее части вместо исходной единичную матрицу.
3. В правой части вспомогательной матрицы на месте единичной получится матрица, обратная данной.
Дата добавления: 2019-09-13; просмотров: 178; Мы поможем в написании вашей работы! |

Мы поможем в написании ваших работ!
