Линейный нейрон и линейные сети

Стр 1 из 3Следующая ⇒

МИНИСТЕРСТВО ОБРАЗОВАНИЯ и НАУКИ РОССИЙСКОЙ ФЕДЕРАЦИИ

Коломенский институт (филиал)

федерального государственного бюджетного образовательного учреждения

высшего образования

«МОСКОВСКИЙ ПОЛИТЕХНИЧЕСКИЙ УНИВЕРСИТЕТ»

Кафедра автоматизации производства и информационных технологий

П.С. Романов

Методические указания по выполнению лабораторной работы

По дисциплине

«СИСТЕМЫ ИСКУССТВЕННОГО ИНТЕЛЛЕКТА»

Исследование нейронных сетей в системе Scilab

Коломна – 2019

Содержание

1.	Введение ....................................................................................................................	2
2.	Основные логические функции и их реализация в электронных устройствах..	2
3.	Линейный нейрон и линейные сети………………………………………………	4
3.1.	Простой нейрон……………………………………………………………………..	4
3.2.	Нейрон с векторным входом……………………………………………………….	5
3.3.	Функции активации…………………………………………………………………	6
3.4.	Персептрон…………………………………………………………………………..	7
3.5.	Структура линейной сети…………………………………………………………..	12
4.	Исследование нейронных сетей в системе Scilab…………………………………	13
4.1.	Функции активации в нейронных сетях в Scilab…………………………………	13
4.2.	Персептрон для логической функции И с двумя входами………………………	14
4.3.	Создание логической функции ИЛИ с двумя входами с использованием нейронной сети Adaline…………………………………………………………….	15
4.4.	Создание логической функции «Исключающее ИЛИ» (XOR) с двумя входами с использованием нейронной сети Madaline………………………………………	17
5.	Задание для лабораторной работы............................................................................	18
6.	Структура отчета.........................................................................................................	18
7.	Литература..................................................................................................................	19

Введение

Лабораторная работа выполняется на основе теоретических положений искусственного интеллекта на ПК с использованием систем Scilab и Microsoft WORD в среде Windows ХР/7/8/10. Цели работы:

знакомство с основными логическими функциями и их реализацией в электронных устройствах;

изучение активационных функций системы Scilab;

изучение модели линейного нейрона и архитектуры линейной нейронной сети;

изучение средств Scilab для исследования нейронных сетей;

получение умений и навыков:

в исследовании активационных функций системы Scilab;

в построении нейронных сетей в Scilab для основных логических функций;

в анализе полученных результатов.

Основные логические функции и их реализация в электронных устройствах

Любые цифровые устройства, включая ЭВМ, состоят из основных логических элементов. К основным логическим элементам относятся физические элементы, реализующие логические функции «ИЛИ», «И», «НЕ», т.е. осуществляющие логические суммирование, умножение и отрицание. Логические элементы предназначены для, выполнения различных логических операций над дискретными сигналами при двоичном способе их представления.

Преимущественное распространение получили логические элементы потенциального типа. В них используются дискретные сигналы, 0 значению которых соответствует уровень низкого потенциала, а значению 1 — уровень высокого потенциала (отрицательного или положительного). Также при описании логических функций (с биполярными входами) применяют следующее обозначение: «-1» соответствует уровень низкого потенциала, а «1» - уровень высокого потенциала.

Логический элемент ИЛИ ( OR ). Логический элемент ИЛИ имеет несколько входов и один общий выход. Условное обозначение биполярного (двухвходового) элемента ИЛИ показано на рис.1, а. Логический элемент ИЛИ выполняет операцию логического сложения (дизъюнкции): Y=x₁ +x₂ +…+x_n , где Y - функция; х₁, х₂,..., х_n — аргументы (переменные, двоичные сигналы на входах).

Здесь функция Y = -1, когда все ее аргументы равны -1, и Y =1 при одном, нескольких или всех аргументах, равных 1. Работу схемы двухвходового логического элемента ИЛИ иллюстрируют таблица истинности, приведенная на рис.1,б.

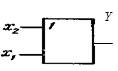
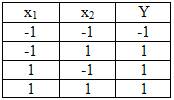
а) б)

Рис.1. Условное обозначение логического элемента ИЛИ (а) и его таблица истинности (б)

Логический элемент И ( AND ). Логический элемент И также имеет несколько входов и один выход. Условное обозначение биполярного (двухвходового) элемента И показано на рис.2,а. Логический элемент И выполняет операцию логического умножения (конъюнкции): Y=x₁∙x₂ ∙…∙x_n, где Y - функция; х₁, х₂,..., х_n — аргументы (переменные, двоичные сигналы на входах).

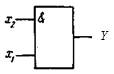
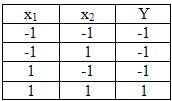
а) б)

Рис.2. Условное обозначение логического элемента И (а) и его таблица истинности (б)

Здесь функция Y =-1, если хотя бы один из ее аргументов равен -1, и Y =1 при всех аргументах, равных 1. Работу схемы двухвходового логического элемента И иллюстрируют таблица истинности, приведенная на рис.2,б.

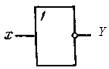
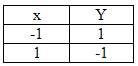
Логический элемент НЕ ( NOT ). Логический элемент НЕ имеет один вход и один выход. Его условное обозначение показано на рис.3,а. Элемент НЕ выполняет операцию инверсии (отрицания), в связи с чем его часто называют логическим инвертором. Сигналу х=1 на входе соответствует Y = -1 и, наоборот, при x=-1 Y =1.

Работу схемы логического элемента НЕ иллюстрируют таблица истинности и временные диаграммы, приведенные на рис.3,б.

а) б)

Рис.3. Условное обозначение логического элемента НЕ (а) и его таблица истинности (б)

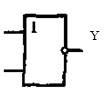
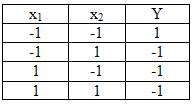
Логический элемент ИЛИ-НЕ ( NOR ). Условное обозначение логического элемента ИЛИ-НЕ показано на рис.4,а. Он объединяет элементы ИЛИ и НЕ с очередностью проведения операций, показанной в таблице истинности рис.4,б. В связи с этим функция Y =-1, если один из ее аргументов равен -1 или оба равны 1, и Y = 1 при всех аргументах, равных -1. Функциональная операция, выполняемая элементом ИЛИ-НЕ при n входах, определяется выражением:

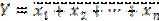, где Y - функция; х₁, х₂,..., х_n — аргументы (переменные, двоичные сигналы на входах).

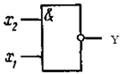
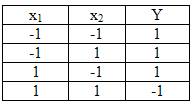
Логический элемент И-НЕ ( NAND ). Условное обозначение логического элемента И-НЕ показано на рис.5,а. Логическая функция элемента И-НЕ при n входах отвечает выражению 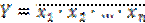, где Y - функция; х₁, х₂,..., х_n — аргументы (переменные, двоичные сигналы на входах).

а) б)

Рис. 4. Условное обозначение логического элемента ИЛИ-НЕ (а), его таблица истинности (б)

Он объединяет элементы И и НЕ с очередностью проведения операций, показанной в таблице истинности рис.5,б. Функция Y = -1 при всех аргументах, равных 1 и Y =1, в остальных случаях.

а) б)

Рис. 5. Условное обозначение логического элемента И-НЕ (а), его таблица истинности (б)

Функция «Исключающее ИЛИ»(XOR – Exclusive - OR ) принимает значение 1, если две ее входные переменные имеют разные логические потенциалы: x₁=1, x₂=-1 ИЛИ x₁=-1, x₂=1. Поэтому ее представляют в следующем виде: 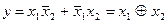, где значок - символизирует функцию «Исключающее ИЛИ». Ей присуще интересное свойство: если на один ее вход подать лог.1, то логический потенциал, поданный на второй вход, будет на выходе инвертирован; если же вместо лог.1 на один вход подать лог.-1, то функция будет вести себя как повторитель логического потенциала, поданного на другой вход. Условное изображение элемента «Исключающее ИЛИ» дано на рис.6. В графическом изображении используется значок m2, указывающий на то, что «Исключающее ИЛИ» функционирует по правилам сложения одноразрядных двоичных чисел (сложение по модулю 2): 1+0=1; 0+1=1; 0+0=0; 1+1=0 (при арифметическом сложении единица переносится в соседний более старший разряд). Операции функции показаны в таблице истинности на рис.6,б.

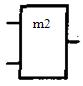
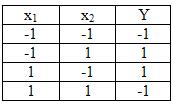
Рис. 6. Условное обозначение логического элемента «Исключающее ИЛИ» (а) и его таблица истинности (б)

Линейный нейрон и линейные сети

Простой нейрон

Элементарной ячейкой нейронной сети является нейрон. Структура нейрона с единственным скалярным входом показана на рис. 7. Скалярный входной сигнал p умножается на скалярный весовой коэффициент W, и результирующий взвешенный вход W·p является аргументом функции активации нейрона f, которая порождает скалярный выход а. Нейрон, показанный на рис. 7, дополнен скалярным смещением b. Смещение суммируется со взвешенным входом W·p и приводит к сдвигу аргумента функции f на величину b. Действие смещения можно свести к схеме взвешивания, если представить, что нейрон имеет второй входной сигнал со значением, равным 1 (b·1). Вход n функции активации нейрона по-прежнему остаётся скалярным и равным сумме взвешенного входа и смещения b.

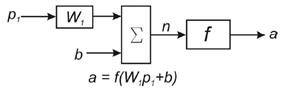
Рис. 7. Структура нейрона с единственным скалярным входом

Эта сумма (W·p + b·1) (1)

является аргументом функции активации f, а выходом функции активации является сигнал а.

Константы W и b являются скалярными параметрами нейрона. Основной принцип работы нейронной сети состоит в настройке параметров нейрона таким образом, чтобы поведение сети соответствовало некоторому желаемому поведению. Регулируя веса и параметры смещения, можно обучить сеть выполнять конкретную работу; возможно также, что сеть сама будет корректировать свои параметры, чтобы достичь требуемого результата.

Уравнение нейрона со смещением имеет вид:

a = f (W·p + b·1) (2)

Как уже отмечалось, смещение b – настраиваемый скалярный параметр нейрона, который не является входом. В этом случае b – вес, а константа 1, которая управляет смещением, рассматривается как вход и может быть учтена в виде линейной комбинации векторов входа:

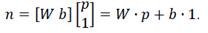(3)

Нейрон с векторным входом

Нейрон с одним вектором входа p с R элементами p₁, p₂,…, p_R показан на рис. 8.

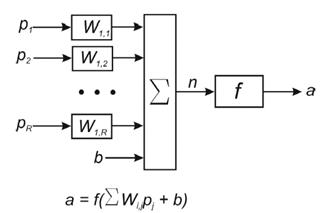
Рис. 8. Нейрон с одним вектором входа

Здесь каждый элемент входа умножается на веса W₁₁, W₁₂,…, W_1R соответственно, и взвешенные значения передаются на сумматор. Их сумма равна скалярному произведению вектора-строки W на вектор-столбец входа p.

Нейрон имеет смещение b, которое суммируется со взвешенной суммой входов. Результирующая сумма:

n = W₁₁·p₁ + W₁₂·p₂ +… + W ₁ _R · p_R + b ·1 или (4)

n = W₁₁p₁ + W₁₂ p₂ +… + W_1R p_R + b (5)

и служит аргументом функции активации f.

В векторном виде это выражение записывается так:

n = W·p + b (6)

Входом n функции активации нейрона служит сумма смещения b и произведение W·p. Эта сумма преобразуется функцией активации f, на выходе которой получаем выход нейрона а, который в данном случае является скалярной величиной.

Функции активации

В современных нейронных сетях наиболее часто применяются следующие виды активационных функций (передаточных функций).

Пороговые активационные функции. Введем пороговую активационную функцию нейрона, представленная на рис.9 с помощью формул:

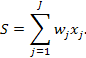
(7)

Выходной сигнал нейрона у может принимать одно из двух значений — нуль или единицу, которые формируются следующим образом:

	у=1, если S³θ;	(8)
	у= 0, если S<θ,	(9)

где θ- порог чувствительности нейрона.

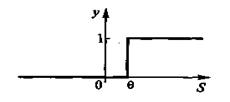
Рис.9. Пороговая активационная функция нейрона

Если в уравнении (7) под S понимать разность между взвешенной суммой входных сигналов и пороговым значением нейрона, т.е.

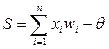то активационная функция у = f(S) будет иметь вид, показанный на рис.10,а. Однако чаще в нейросетях применяется пороговая функция, симметричная относительно начала координат (рис.10,б).

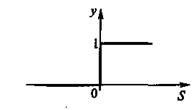
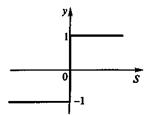
а) б)

Рис.10. Пороговые активационные функции с несимметричной (а) и симметричной (б)

областями изменения

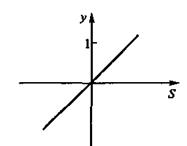
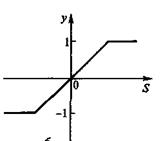
Линейные активационные функции. На рис.11,а показан график линейной активационной функции у = S с неограниченной областью изменения. Такие функции могут быть и с ограниченной областью изменения: у=-1 при S<-1; у=S при -1£S£1; у=1 при S>1 (рис.11,б).

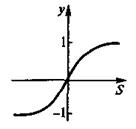
Сигмоидные (логистические) активационные функции. На рис.12,а изображен график сигмоидной функции, заданной уравнением

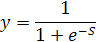
а на рис.12,б — уравнением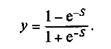

а) б)

Рис.11. Линейные активационные функции: с неограниченной (а) и ограниченной (б)

областями изменения

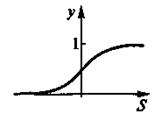
а) б)

Рис.12. Сигмоидные активационные функции с несимметричной (а) и симметричной (б)

областями изменения

Аналогичный последнему графику характер имеют функции арктангенса

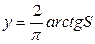
и гиперболического тангенса у=thS, a также функция

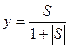которые тоже называют сигмоидами.

Персептрон

Нейрон, используемый в модели персептрона (нейрон, предложенный Мак-Каллока – Питтса в 1943 г.), имеет ступенчатую функцию активации с жёсткими ограничениями (рис.13, использовано упрощённое изображение нейрона).

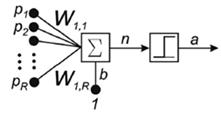
Рис.13. Нейрон, используемый в модели персептрона

Каждое значение элемента вектора входа персептрона умножено на соответствующий вес W_1j, и сумма полученных взвешенных элементов является входом функции активации. Если вход функции активации n ≥ 0, то нейрон персептрона возвращает 1, если n < 0, то 0.

Функция активации с жёсткими ограничениями придаёт персептрону способность классифицировать векторы входа, разделяя пространство входов на две области, как это показано на рис. 14, для персептрона с двумя входами и смещением. Пространство входов делится на две области разделяющей линией L, которая для двумерного случая задаётся уравнением: W _m ·p + b = 0 (10)

Эта линия перпендикулярна к вектору весов W и смещена на величину b. Векторы входа выше линии L соответствуют положительному потенциалу нейрона, и, следовательно, выход персептрона для этих векторов будет равен 1; векторы входа ниже линии L соответствуют выходу персептрона, равному 0. При изменении значений смещения и весов граница линии L изменяет свое положение.

Персептрон без смещения всегда формирует разделяющую линию, проходящую через начало координат; добавление смещения формирует линию, которая не проходит через начало координат. В случае, когда размерность вектора входа превышает 2, т.е. входной вектор p имеет более 2 элементов, разделяющей границей будет служить гиперплоскость.

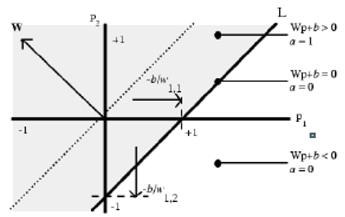
Рис. 14. Функция активации персептрона с двумя входами и смещением

Адалайн, мадалайн и обобщенное дельта-правило. Круг решаемых задач значительно расширится, если научить персептрон выдавать не только бинарные выходные сигналы типа ноль и единица, но и аналоговые, т.е. имеющие непрерывные значения. Такое обобщение персептрона было сделано Уидроу и Хоффом, которые вместо ступенчатой ввели непрерывную нелинейную функцию активации (рис.12):

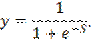
Эту функцию назвали сигмоидой из-за того, что ее графическое изображение напоминает латинскую букву «S». Другое название сигмоиды — логистическая функция.

Подобно обычной пороговой функции активации, сигмоида отображает точки области определения (-¥, +¥) на интервал (0, +1). Практически сигмоида обеспечивает непрерывную аппроксимацию классической пороговой функции. Для сигмоиды принято обозначение у =f_σ(S).

Персептроны с сигмоидными активационными функциями с одним выходом назвали адалайн, с несколькими выходами — мадалайн (от английских слов ADAptiveLinearNEuron и Many ADALINE).

Появление персептронов с непрерывными активационными функциями обусловило и новые подходы к их обучению. Уидроу и Хофф предложили минимизировать среднеквадратичную ошибку, определяемую как разность между требуемыми d_i и реальными y_i выходными сигналами персептрона:

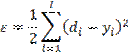
Рассмотрим алгоритм коррекции весовых коэффициентов персептрона, имеющего J входов и I выходов (рис.15). Среднеквадратичная ошибка ε является многомерной функцией весовых коэффициентов, т.е. ε= ε(w_i_j), и в пространстве координат w_i_j представляется в виде некоторой многомерной поверхности — гиперповерхности. Если оставить только две оси координат, например w₁₁ и w₁₂, то эта поверхность будет иметь вид фигуры, напоминающей параболоид, который, однако, может иметь как один, так и несколько минимумов. Поэтому такую поверхность будем называть псевдопараболоидом. Обучение персептрона можно представить как задачу отыскания такого сочетания весовых коэффициентов w_i_j, которому соответствует самая нижняя точка гиперпсевдопараболоида. Такую задачу называют оптимизационной и говорят, что она состоит в минимизации функционала ε= ε(w_i_j) в пространстве параметров w_i_j.

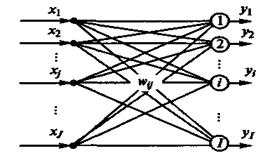
Рис. 15. Однослойный персептрон с J входами и I выходами

Существует множество методов решения оптимизационных задач. Наиболее простым является случайный перебор весовых коэффициентов w_ij с последующими вычислениями и сравнениями между собой соответствующих этим коэффициентам функций ошибок ε. Однако более эффективным является метод градиентного спуска, согласно которому изменение (коррекция) каждого весового коэффициента Δw_ij производится в сторону, противоположную градиенту поверхности гиперпсевдопараболоида, т.е.

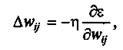
где η - коэффициент скорости обучения.

Среднеквадратичная ошибка ε является сложной функцией, зависящей, в первую очередь, от выходных сигналов персептрона y_i поэтому в результате вычислений получим:

Δw_ij =η(d_i – y_i)f_σ(S_i)(1- f_σ(S_i))x_j = η(d_i – y_i)y_i(1- y_i)x_j,

где y_i=f_σ(S_i), S_i= .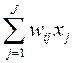

Итерационная формула для обучения однослойного персептрона:

w_ij(t+1)= w_ij(t)+ Δw_ij,

в которой Δw_ij =ηδ_ix_j; δ_i =(d_i – y_i)y_i(1- y_i).

Этот алгоритм называют обобщенным дельта-правилом, преимущество которого состоит в более быстрой сходимости и возможности более точной обработки входных и выходных непрерывных сигналов, т.е. в расширении круга решаемых персептронами задач и возможности получения более точных и качественных решений.

Ограниченность однослойного персептрона. Было установлено, что какие бы значения ни придавались весам и порогу, персептрон в принципе не способен воспроизвести соотношение между входами и выходом, требуемое для представления функции «Исключающее ИЛИ». Такие задачи получили название линейно неразделимых.

Многослойный персептрон и алгоритм обратного распространения ошибки.

Оказалось, что проблему «Исключающее ИЛИ» можно решить с помощью двухслойного персептрона, изображенного на рис.16.

Работа этого персептрона происходит по следующему алгоритму.

Нейрон № 1: S₁=0,5х₁ + (-0,5)х₂;y₁= 1, еслиS₁³θ; y₁= 0, еслиS₁<θ.

Нейрон № 2: S₂=(-0,5)x₁ +0,5x₂;у₂ = 1, если S₂³θ; у₂ = 0, если S₂<θ.

Нейрон № 3: S₃=l×x_l+l×x₂;y₃ = 1, если S₃³θ; y₃= 0, если S₃<θ.

С помощью этих формул легко проверить таблицу истинности персептрона, составленную при задании порога θ= 0,5 (табл.1).

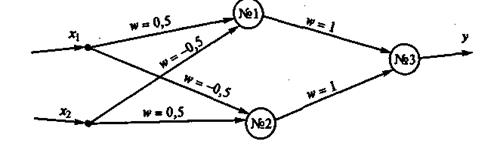
Рис.16. Двухслойный персептрон, реализующий функцию «Исключающее ИЛИ»

Таблица 1

Таблица истинности двухслойного персептрона (см. рис.16)

x₁	x₂	S₁	S₂	y₁	y₂	S₃	y₃	y
0	0	0	0	0	0	0	0	0
0	1	-0,5	0,5	0	1	1	1	1
1	0	0,5	-0,5	1	0	1	1	1
1	1	0	0	0	0	0	0	0

Эффективный алгоритм обучения многослойных персептронов, открывший путь для их широкого практического применения, стал известен только в 1986 г., благодаря работе Румельхарта, Хилтона и Вильямса, называемый алгоритмом обратного распространения ошибки (backpropagation).

Рассмотрим идею алгоритма обратного распространения ошибки, попытавшись обобщить дельта-правило для случая обучения двухслойного персептрона, имеющего N входов, I выходов и скрытый слой из J нейронов (рис.17). Алгоритм корректировки синаптических весов нейронов выходного слоя оставим таким же, как для однослойного персептрона, заменив x_j на у_j .

	w_ij(t+1) = w_ij(t) + Δw_ij;	(10)
	Δw_ij=ηδ_iy_j;	(11)
	δ_i =(d_i – y_i)y_i(1- y_i).	(12)

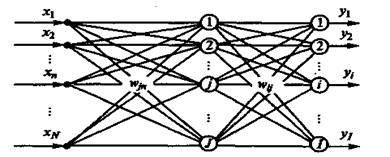
Рис. 17. Двухслойный персептрон с N входами, I выходами и

скрытым слоем из J нейронов

Синаптические веса нейронов скрытого слоя попытаемся корректировать с помощью тех же самых формул, в которых индекс i заменим на j, а индекс j - на n:

	Δw_jn=ηδ_jy_n;	(13)
	δ_j =(d_j – y_j)y_j(1- y_j).	(14)

Понятно, что в последнем выражении в качестве у_n следует использовать х_n. Однако неясным здесь остается вопрос о вычислении нейронной ошибки (d_j - y_j), которая для скрытого слоя неизвестна. Идея авторов рассматриваемого алгоритма состояла в том, чтобы в качестве этой ошибки использовать суммарные ошибки с выходного слоя, помноженные на силы соответствующих синаптических связей, т.е.

(d_j – y_j) =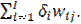

(15)

Итак, для скрытого слоя окончательно имеем:

	Δw_jn=ηδ_jx_n;	(16)
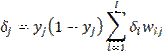
		(17)

Используя эту идею, несложно расписать алгоритм обратного распространения ошибки для обучения персептрона, имеющего произвольное число скрытых слоев. Однако прежде внесем еще одно изменение в модель нейрона. К сумме, которую вычисляет нейрон, полезно добавить некоторое число, называемое порогом, или смещением:

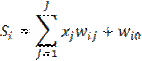
(18)

Смещение w_i₀ задается так же, как и синаптические веса w_ij, т.е. датчиком случайных чисел. Ввод смещения в формулу преобразования нейрона можно интерпретировать как добавление еще одного входного сигнала x₀, который всегда равен единице. Поэтому, чтобы не усложнять выкладки, сумму (18) представим в более компактном виде (приняв x₀= 1):

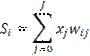
(19)

Алгоритм обратного распространения ошибки распишем для многослойного персептрона, имеющего входной слой k= 0, несколько скрытых слоев k=1,2,...,К-1 и выходной слой k=K (рис.18). Нейроны входного слоя математических преобразований не выполняют, а лишь передают входные сигналы нейронам первого слоя.

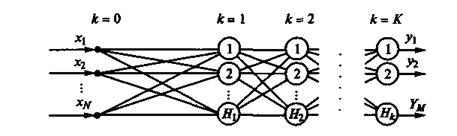
Рис.18. Многослойный персептрон (MLP -MultiLayerPerseptron)

Будем полагать, что каждый k-й слой содержит H_k нейронов. Таким образом, персептрон имеет N =H₀ входов и М= H_К выходов. В алгоритме будем использовать следующие обозначения: i- порядковый номер нейрона k-го слоя; j- порядковый номер нейрона (k-1)-го слоя; l- порядковый номер нейрона (k+1)-го слоя.

Шаг 1. Инициализация синаптических весов и смещений.

В циклах по k=1,2,...,К; i=1,2,...,H_k; j =1,2,...,Н_k_-1синаптическим весам и смещениям w_ij⁽^k⁾ датчиком случайных чисел присваиваются малые величины, например, из интервала от -1 до 1.

Шаг 2. Представление из обучающей выборки очередного входного вектора X_q=(х₁,х₂,...,x_N)_q и соответствующего ему желаемого выходного вектора D_q=(d₁,d₂, ...,d_M)_q, где q - номер примера в обучающей выборке.

Шаг 3. Прямой проход.

В циклах по k=1,2,...,К; i=1,2,...,Н_k вычисляются выходные сигналы i-го нейрона в k-м слое

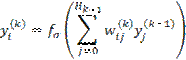
(20)

где y_j⁽⁰⁾ =x_j, x₀=1, y_j⁽^k^-1) = 1 и выходные сигналы персептрона y_i=y_i⁽^K⁾.

Шаг 4. Обратный проход.

В циклах по k= К,К-1,...,1; i=1,2,...,H_k;j=1,2, ...,H_k_-1 вычисляются синаптические веса на новой эпохе

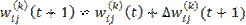(21)

где

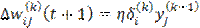(22)

причем для выходного слоя k= К согласно (12):

δ_i^(K) =(d_i – y_i)y_i(1- y_i),

а для всех других случаев согласно (17)

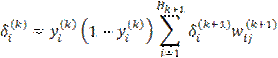
(23)

Шаг 5. Повторение шагов 2 - 4 необходимое число раз.

Входные векторы обучающих примеров Х_q и D_q на втором шаге алгоритма обычно представляются последовательно от первого до последнего, т.е. q=1,2,...,Q, где Q - общее число примеров. Например, в случае распознавания букв русского алфавита Q=33. После того как для каждого обучающего примера будут скорректированы весовые коэффициенты персептрона, т.е. шаги 2-4 будут повторены 33 раза, на пятом шаге алгоритма вычисляется среднеквадратичная ошибка, усредненная по всем обучающим примерам:

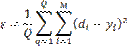
(24)

Помимо среднеквадратичной ошибки может быть также оценена максимальная разность между желаемым и фактическим выходами персептрона:

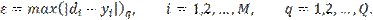
(25)

Итерационный процесс заканчивается после того, как погрешность ε, вычисляемая по формулам (24) или (25), достигнет заданной величины, либо при достижении предельного числа эпох обучения. В результате персептрон обучится выполнять нужное отображение любого входного вектора Х_q на выходной вектор Y_q, отличающийся от желаемого вектора D_q на некоторую малую величину.

Теперь представим себе, что на входное табло фотоэлементов попала карточка с какой-либо буквой, выполненной другим шрифтом. Фотоэлементы сформируют входной вектор X, не совпадающий ни с одним из векторов из использованной обучающей выборки. Если шрифт, которым выполнена входная буква не слишком отличается от шрифта обучающей выборки, а персептрон хорошо спроектирован и обучен, то он вычислит вектор Y, в котором выход нейрона, соответствующего представленной на вход букве, будет иметь максимальное значение. Таким образом, персептрон, несмотря на помехи и искажения входного образа, выдаст правильное заключение о его принадлежности к тому или иному классу. Свойство персептрона правильно реагировать на входные образы, которых не было в обучающей выборке, называется свойством обобщения.

Структура линейной сети

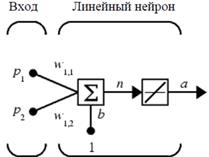
Линейные сети по своей структуре аналогичны персептрону и отличаются лишь функцией активации. Выход линейной сети может принимать любое значение, в то время как выход персептрона ограничен значениями 0 или 1. На рис.19,а показан линейный нейрон с двумя входами. Он имеет структуру, сходную со структурой персептрона. Единственное отличие состоит в том, что используется линейная функция активации. Весовая матрица W в этом случае имеет только одну строку, и выход сети определяется выражением:

a = f(n) = f(Wp+b) =Wp+b = w₁₁p₁ + w₁₂p₂ +b

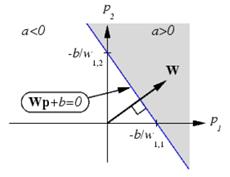
Подобно персептрону, линейная сеть задает в пространстве входов разделяющую линию, на которой функция активации n равна 0 (рис. 19,б). Векторы входа, расположенные выше этой линии, соответствуют положительным значениям выхода, а расположенные ниже – отрицательным. Это означает, что линейная сеть может быть применена для решения задач классификации. Однако такая классификация может быть выполнена только для класса линейно отделимых объектов. Таким образом, линейные сети имеют то же самое ограничение, что и персептрон.

а) б)

Рис. 19 Линейный нейрон с двумя входами (а), линейная сеть в пространстве входов (б)

Нейронная сеть формируется путем соединения многих нейронов. Типичная нейронная сеть состоит из 3 слоев: входной слой, скрытый слой и выходной слой. Входной слой может быть набором объектов, извлеченных из объектов, подлежащих классификации. Затем скрытый слой воздействует на такой набор, а затем передает результат на выходной слой.

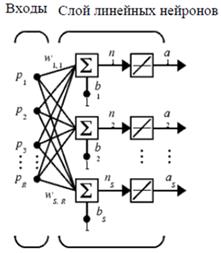
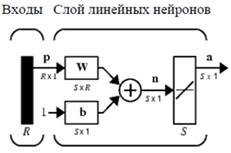
Архитектура сети. Линейная сеть, показанная на рис.20,а, включает S нейронов, размещенных в одном слое и связанных с R входами через матрицу весов W. На рис.20,б показана укрупненная структурная схема этой сети, вектор выхода а которой имеет размер S×1.

а) б)

Рис. 20. Линейная сеть: а) с S нейронами, размещенными в одном слое; б) укрупненная структурная схема этой сети

Дата добавления: 2019-09-13; просмотров: 2317; Мы поможем в написании вашей работы!

Поделиться с друзьями:

12 3 Следующая ⇒

Мы поможем в написании ваших работ!