Интегральный признак Коши-Маклорена
(Маклорен Колин (1698 – 1746) – шотландский математик, ученик
И.Ньютона.)
Теорема 14. Если функция  неотрицательна и не возрастает на промежутке
неотрицательна и не возрастает на промежутке 
 то ряд:
то ряд:
 (3.3)
(3.3)
и несобственный интеграл:
 (3.4)
(3.4)
– сходятся или расходятся одновременно.
Если ряд (3.3) и интеграл (3.4) сходятся, то справедливы следующие оценки:
 (3.5)
(3.5)
 (3.6)
(3.6)
где 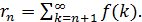 Заметим, что оценка сверху в неравенстве (3.6) является следствием оценки сверху в неравенстве (3.5).
Заметим, что оценка сверху в неравенстве (3.6) является следствием оценки сверху в неравенстве (3.5).
Пример 44. Рассмотрим обобщенный гармонический ряд 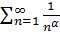 ,
, 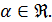
При  0 функция
0 функция  положительна, убывает на промежутке
положительна, убывает на промежутке 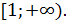 При
При 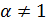 имеем:
имеем:

Рассмотрим три случая:
1) если 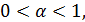 то при
то при  следовательно,
следовательно,  т.е. интеграл расходится, а значит расходится и ряд (это мы установили выше другим способом);
т.е. интеграл расходится, а значит расходится и ряд (это мы установили выше другим способом);
2) если  , то исходный ряд превращается в гармонический ряд, расходимость которого была доказана в п. 1.1, (впрочем, интеграл
, то исходный ряд превращается в гармонический ряд, расходимость которого была доказана в п. 1.1, (впрочем, интеграл  также расходится);
также расходится);
3) если  , то ряд
, то ряд  следовательно,
следовательно, 
 т.е. несобственный интеграл сходится, а значит и ряд сходится.
т.е. несобственный интеграл сходится, а значит и ряд сходится.
Если  , то ряд
, то ряд 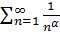 расходится, так как в этом случае не выполнено необходимое условие сходимости ряда:
расходится, так как в этом случае не выполнено необходимое условие сходимости ряда: 
|
|
|
Итак, ряд 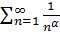 сходится при
сходится при  и расходится при
и расходится при  .
.
Пример 45. Исследовать на сходимость ряд  .
.
Введем функцию  На промежутке
На промежутке  эта функция принимает положительные значения, а ее производная равна
эта функция принимает положительные значения, а ее производная равна
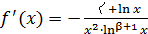 . Если
. Если  т.е.
т.е. 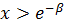 , то
, то  . Следовательно,
. Следовательно,  положительная функция и убывает на промежутке
положительная функция и убывает на промежутке 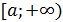 , где
, где
 . Рассмотрим несобственный интеграл:
. Рассмотрим несобственный интеграл:
 .
.
Из последнего равенства видно, что данный интеграл сходится, если 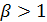 , и расходится, если
, и расходится, если  .
.
Следовательно, исследуемый ряд сходится при 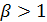 и расходится при
и расходится при  .
.
Пример 46. Исследовать на сходимость ряд  .
.
В этом случае непосредственное применение интегрального признака нецелесообразно, т.к. вычисление несобственного интеграла может оказаться затруднительным. Сравним общий член данного ряда с общим членом ряда
 . Найдем:
. Найдем:

Так как ряд  расходится (см. предыдущий пример), то по предельному признаку сравнения исходный ряд также расходится.
расходится (см. предыдущий пример), то по предельному признаку сравнения исходный ряд также расходится.
Пример 47. Исследовать сходимость ряда 
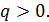
Так как  если
если  то в силу теоремы сравнения данный ряд расходится при
то в силу теоремы сравнения данный ряд расходится при 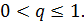
Пусть  . Так как по правилу Лопиталя
. Так как по правилу Лопиталя  при
при  , то, в частности, для
, то, в частности, для 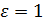 найдется номер
найдется номер 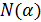 , такой, что
, такой, что 
 Число
Число  запишем следующим образом:
запишем следующим образом:  , где
, где  Тогда
Тогда  , и так как обобщенный гармонический ряд
, и так как обобщенный гармонический ряд 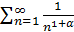 при
при  сходится, то в силу теоремы сравнения и исходный ряд сходится для всех значений
сходится, то в силу теоремы сравнения и исходный ряд сходится для всех значений 
|
|
|
Вывод: ряд  сходится для всех значений
сходится для всех значений  и
и  ; кроме того, этот ряд сходится и для значений
; кроме того, этот ряд сходится и для значений  (см. пример 45).
(см. пример 45).
Пример 48. Выясним, сколько членов ряда  надо сложить, чтобы найти сумму этого ряда с точностью до 0,001.
надо сложить, чтобы найти сумму этого ряда с точностью до 0,001.
Введем функцию  ,
, 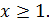 по формуле (3.6)
по формуле (3.6)
 или
или 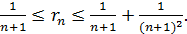 Так как требуемая погрешность не должна превосходить 0,001, то потребуем, чтобы
Так как требуемая погрешность не должна превосходить 0,001, то потребуем, чтобы  Тогда при
Тогда при  значит для вычисления суммы ряда с требуемой точностью следует сложить по меньшей мере 1000 членов ряда! Как видим, сходимость ряда весьма «медленная».
значит для вычисления суммы ряда с требуемой точностью следует сложить по меньшей мере 1000 членов ряда! Как видим, сходимость ряда весьма «медленная».
Замечание. При решении данной задачи можно было воспользоваться и оценкой (3.5).
3.5. Метод выделения главной части
При исследовании на сходимость ряда  с неотрицательными членами полезны асимптотические формулы вида:
с неотрицательными членами полезны асимптотические формулы вида:
 (3.7)
(3.7)
 (3.8)
(3.8)
В случае (3.7) ряд  сходится при
сходится при  и расходится при
и расходится при  ; в случае (3.8) ряд
; в случае (3.8) ряд  сходится, если
сходится, если  или
или 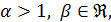 и в других случаях расходится.
и в других случаях расходится.
Пример 49. Исследовать сходимость ряда 
|
|
|
Здесь  при
при 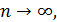 так как последовательность
так как последовательность  является бесконечно малой при
является бесконечно малой при  ряд с общим членом
ряд с общим членом  согласно (3.8) расходится, поэтому ряд также расходится.
согласно (3.8) расходится, поэтому ряд также расходится.
Пример 50. Исследовать сходимость ряда  Общий член данного ряда
Общий член данного ряда  Здесь
Здесь  и согласно (3.8) исходный ряд сходится.
и согласно (3.8) исходный ряд сходится.
Пример 51. Исследовать сходимость ряда  Заметим, что при
Заметим, что при  предел
предел 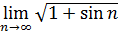 не существует, так как не существует предел
не существует, так как не существует предел  ; если
; если  то
то 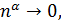
 не существует, и общий член ряда не стремится к нулю. Следовательно, при
не существует, и общий член ряда не стремится к нулю. Следовательно, при  ряд расходится. При
ряд расходится. При  Так как
Так как 
 , то
, то  Согласно (3.7) данный ряд сходится при
Согласно (3.7) данный ряд сходится при  и расходится при
и расходится при 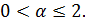
Окончательно получаем: исходный ряд сходится при 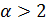 и расходится при
и расходится при 
Пример 52. Исследовать сходимость ряда 
Используя разложения:

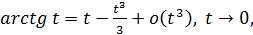 находим
находим 
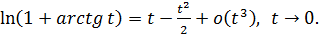 Следовательно,
Следовательно,  т.е.
т.е. 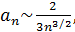 и поэтому ряд сходится.
и поэтому ряд сходится.
4. Знакопеременные ряды
Знакопеременный ряд – это ряд, членами которого являются вещественные числа произвольного знака.
Определение. Ряд
 (2.1)
(2.1)
называется абсолютно сходящимся, если сходится ряд, составленный из модулей его членов:
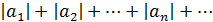 (2.2)
(2.2)
|
|
|
Определение. Сходящийся ряд (2.1) называют условно сходящимся, если ряд (2.2) расходится.
4.1. Свойства абсолютно и условно сходящихся рядов
Теорема 15. Если ряд (2.1) абсолютно сходится, то он сходится, причем имеет место неравенство:

Теорема 16. Сумма абсолютно сходящегося ряда равна разности сумм двух положительных рядов, составленных соответственно из всех положительных членов ряда и из абсолютных величин всех его отрицательных членов.
Теорема 17 (признак сравнения). Если существует сходящийся ряд с положительными членами  , такой, что
, такой, что  , то ряд
, то ряд  сходится абсолютно.
сходится абсолютно.
Пример 53. Доказать, что ряд  абсолютно сходится.
абсолютно сходится.
Воспользуемся известными неравенствами: 
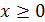 и
и  ,
, 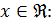
 , откуда и следует абсолютная сходимость заданного ряда.
, откуда и следует абсолютная сходимость заданного ряда.
4.1.1. Сочетательное свойство для числовых рядов.
Посмотрим, как влияет на сходимость ряда группировка его членов.
Пример 54. Сгруппируем формально члены следующего ряда по два, начиная с первого:

Если же формально сгруппировать члены этого же ряда по два, начиная со второго, то получим:

Пример показывает, что группировка членов расходящегося ряда может привести к разным результатам.
В общем случае перепишем ряд 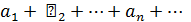 в виде
в виде

где

Обозначим  Ряд
Ряд

называют группировкой ряда 
Теорема 18. Если исходный ряд  сходится, то любая его группировка
сходится, то любая его группировка  также сходится, причем к той же сумме, которую имеет исходный ряд:
также сходится, причем к той же сумме, которую имеет исходный ряд:  .
.
Замечание. Обратное утверждение неверно. Рассмотрим ряд  . Если
. Если 
 то
то  в то время как исходный ряд
в то время как исходный ряд  расходится. Однако справедлива следующая теорема.
расходится. Однако справедлива следующая теорема.
Теорема 19. Пусть  а последовательность натуральных чисел
а последовательность натуральных чисел  возрастает:
возрастает:


Тогда ряд  сходится или расходится одновременно с любой его группировкой
сходится или расходится одновременно с любой его группировкой  .
.
Пример 55. Рассмотрим ряд  Этот ряд может быть просуммирован группировкой по два члена:
Этот ряд может быть просуммирован группировкой по два члена:  Так как
Так как

то рассматриваемый ряд сходится. Поскольку гармонический ряд расходится,
то знакопеременный гармонический ряд сходится условно.
4. 1. 2. Переместительное свойство сходящихся рядов
Одним из важнейших свойств суммы конечного числа вещественных слагаемых является переместительное свойство. Естественно возникает вопрос, остается ли справедливым это свойство для суммы сходящегося ряда.
Определение. Если отображение  является биекцией множества N натуральных чисел на себя, то ряд
является биекцией множества N натуральных чисел на себя, то ряд 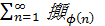 называется перестановкой ряда
называется перестановкой ряда  .
.
Пример 56. Рассмотрим условно сходящийся ряд:
 .
.
Перестать и сгруппируем члены ряда по три следующим образом:

сумма которого равна:  .
.
Таким образом, перестановка членов условно сходящегося ряда изменяет его сумму. В данном случае она уменьшилась вдвое. Рассмотренный пример показывает, что условно сходящийся ряд не обладает переместительным свойством. Полную ясность в вопрос о сходимости перестановки условно сходящегося ряда вносит следующее утверждение.
Теорема 21 (Коши). Если ряд сходится абсолютно, то любая его перестановка также сходится абсолютно, причем к той же сумме.
Рассмотрим ряд  , общий член которого может быть представлен в виде произведения:
, общий член которого может быть представлен в виде произведения:  . Приведем достаточные признаки сходимости таких рядов.
. Приведем достаточные признаки сходимости таких рядов.
Теорема 22 (признак Абеля). Пусть дан ряд  . Если последовательность
. Если последовательность  монотонна и ограничена, а ряд
монотонна и ограничена, а ряд  сходится, то ряд
сходится, то ряд  сходится.
сходится.
(Абель Нильс Хенрик(1802–1829) – норвежский математик, один из крупнейших математиков 19 века.)
Теорема 23 (признак Дирихле). Пусть дан ряд  . Если последовательность частичных сумм ряда
. Если последовательность частичных сумм ряда  ограничена, а последовательность
ограничена, а последовательность  , начиная с некоторого номера, монотонно стремится к нулю, то ряд
, начиная с некоторого номера, монотонно стремится к нулю, то ряд 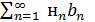 сходится.
сходится.
( Дирихле Петер Густав Лежён (1805–1859) – немецкий математик.)
На практике при применении признаков Абеля и Дирихле в качестве последовательности 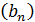 чаще всего берется или последовательность
чаще всего берется или последовательность  , или одна из последовательностей
, или одна из последовательностей  и
и  .
.
Пример 57. Пусть последовательность  монотонно стремится к нулю. Тогда ряд
монотонно стремится к нулю. Тогда ряд  сходится при любом
сходится при любом  , а ряд
, а ряд  сходится при любом
сходится при любом  .
.
Так как
 ,
,  ,
,
 то обе суммы ограничены по абсолютной величине числом
то обе суммы ограничены по абсолютной величине числом  . По признаку Дирихле оба ряда сходятся при
. По признаку Дирихле оба ряда сходятся при  впрочем, первый ряд сходится и при
впрочем, первый ряд сходится и при  ибо все его члены обращаются в нуль.
ибо все его члены обращаются в нуль.
В частности, например, сходятся ряды:
 ,
,  ,
,  и т.п.
и т.п.
Пример 58. Рассмотрим ряд  .
.
Оценка  не дает информации о поведении ряда
не дает информации о поведении ряда  . Покажем, что исходный ряд сходится. Положим
. Покажем, что исходный ряд сходится. Положим  и
и  . Ряд
. Ряд  сходится условно, а последовательность
сходится условно, а последовательность  монотонна
монотонна  и ограничена
и ограничена  . Поэтому в силу признака Абеля исходный ряд сходится. Расходимость ряда
. Поэтому в силу признака Абеля исходный ряд сходится. Расходимость ряда  , составленного из модулей членов данного ряда, следует из неравенства
, составленного из модулей членов данного ряда, следует из неравенства  и расходимости ряда
и расходимости ряда  . В самом деле, так как
. В самом деле, так как  и так как ряд
и так как ряд 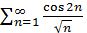 сходится, а ряд
сходится, а ряд  расходится, то ряд
расходится, то ряд  расходится. Поэтому в силу теоремы сравнения расходится и ряд
расходится. Поэтому в силу теоремы сравнения расходится и ряд  . Итак, ряд
. Итак, ряд  сходится условно.
сходится условно.
Заметим, что ряд  также сходится условно.
также сходится условно.
4. 2. Знакочередующиеся ряды
Определение. Знакопеременный ряд называют знакочередующимся, если каждые два соседних члена этого ряда имеют противоположные знаки.
Обычно знакочередующийся ряд записывают в виде:

 (2.3)
(2.3)
Укажем очень простой достаточный признак сходимости знакочередующегося ряда, принадлежащий Лейбницу. (Лейбниц Готфрид Вильгельм(1646–1716) – немецкий математик, физик и изобретатель, юрист, историк, философ-идеалист, языковед.)
Теорема (признак Лейбница). Пусть члены знакочередующегося ряда
(2.3) удовлетворяют условиям:
1) 

2) 
Тогда ряд (2.3) сходится и для его суммы S справедливо неравенство:
 .
.
Следствие: Пусть  - остаток ряда (2.3) и пусть выполнены условия 1) и 2) признака Лейбница. Тогда любой остаток ряда не превосходит по абсолютной величине первого из своих членов:
- остаток ряда (2.3) и пусть выполнены условия 1) и 2) признака Лейбница. Тогда любой остаток ряда не превосходит по абсолютной величине первого из своих членов:  ,
,  и имеет одинаковый с ним знак:
и имеет одинаковый с ним знак:  .
.
Замечание. Признак Лейбница является следствием признака Дирихле.
Пример 59. Исследовать на сходимость ряд  .
.
Покажем, что ряды, начиная с некоторого номера, убывают по абсолютной величине. Имеем  . Так как
. Так как  при
при  , то, начиная с номера
, то, начиная с номера  , выполняется неравенство
, выполняется неравенство  . Кроме того,
. Кроме того,  условия теоремы Лейбница выполнены, следовательно, ряд сходится. Затем, что ряд
условия теоремы Лейбница выполнены, следовательно, ряд сходится. Затем, что ряд  , составленный из модулей членов данного ряда, расходится, так как
, составленный из модулей членов данного ряда, расходится, так как 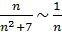 ,
,  . Поэтому исходный ряд сходится условно.
. Поэтому исходный ряд сходится условно.
Пример 60. Исследовать на сходимость ряд 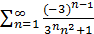 .
.
Рассмотрим ряд, составленный из абсолютных величин членов исходного ряда:  . Сравним его со сходящимся рядом
. Сравним его со сходящимся рядом  :
:
 .
.
Предел конечен и отличен от нуля, следовательно, ряд  ведет себя так же, как и ряд
ведет себя так же, как и ряд  , т.е. сходится. Тогда по теореме 15 исходный ряд сходится, причем абсолютно.
, т.е. сходится. Тогда по теореме 15 исходный ряд сходится, причем абсолютно.
Пример 61. Покажем, что ряд  расходится. Так как
расходится. Так как  то общий член ряда не стремится к нулю. Необходимое условие сходимости ряда не выполнено, и поэтому исходный ряд расходится.
то общий член ряда не стремится к нулю. Необходимое условие сходимости ряда не выполнено, и поэтому исходный ряд расходится.
Замечание. Для сходимости знакочередующегося ряда выполнение признака Лейбница не является необходимым условием: знакочередующийся ряд может сходиться, даже если модуль его общего члена стремится к нулю не монотонно.
Так ряд 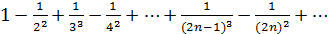 сходится и притом абсолютно, хотя признак Лейбница и не выполнен: абсолютная величина об-щего члена ряда хотя и стремится к нулю, но не монотонно.
сходится и притом абсолютно, хотя признак Лейбница и не выполнен: абсолютная величина об-щего члена ряда хотя и стремится к нулю, но не монотонно.
Пример 62. Исследовать сходимость ряда  .
.
Так как по правилу Лопиталя
 и
и
 при
при  то выполнены соответственно условия 1) и 2) признака Лейбница. Поэтому данный ряд сходится. Заметим, что ряд, составленный из абсолютных величин членов данного ряда, расходится:
то выполнены соответственно условия 1) и 2) признака Лейбница. Поэтому данный ряд сходится. Заметим, что ряд, составленный из абсолютных величин членов данного ряда, расходится:  Поэтому ряд
Поэтому ряд  сходится условно.
сходится условно.
Пример 63. Рассмотрим ряд 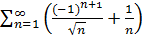 .
.
Ряд  сходится в силу признака Лейбница, гармонический ряд
сходится в силу признака Лейбница, гармонический ряд  расходится, следовательно, данный ряд расходится. В тоже время
расходится, следовательно, данный ряд расходится. В тоже время  ,
,  . Поэтому делать вывод о сходимости или расхо-димости ряда
. Поэтому делать вывод о сходимости или расхо-димости ряда  по поведению ряда
по поведению ряда  где
где  ,
,  , можно
, можно
только для рядов с неотрицательными членами!
Пример 64. Рассмотрим ряд  .
.
Используя асимптотическую формулу  ,
,  получаем
получаем  , где
, где  ,
,  Так как ряд
Так как ряд  сходится абсолютно, а ряд
сходится абсолютно, а ряд  в силу признака Лейбница сходится условно, то заданный ряд сходится условно.
в силу признака Лейбница сходится условно, то заданный ряд сходится условно.
Пример 65. Вычислить приближенно с точностью до  сумму зна-кочередующегося ряда:
сумму зна-кочередующегося ряда:

Сходимость ряда следует из признака Лейбница. Так как для сходящегося ряда его сумма  , то при достаточно больших n можно считать, что
, то при достаточно больших n можно считать, что  , причем для остатка ряда справедлива оценка
, причем для остатка ряда справедлива оценка
 .
.
В данном примере  . По условию задачи должно выпол-няться неравенство
. По условию задачи должно выпол-няться неравенство  . Эта оценка удовлетворяется уже при
. Эта оценка удовлетворяется уже при 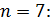

Следовательно, для решения задачи можно отбросить все члены ряда, начиная с  , и вычислить сумму только первых семи членов. Для того чтобы гарантировать требуемую точность, будем вычислять каждое слагаемое с шестью знаками после запятой, делая округление на шестом знаке. При такой точности вычислений ошибка при подсчете каждого слагаемого будет меньше, чем
, и вычислить сумму только первых семи членов. Для того чтобы гарантировать требуемую точность, будем вычислять каждое слагаемое с шестью знаками после запятой, делая округление на шестом знаке. При такой точности вычислений ошибка при подсчете каждого слагаемого будет меньше, чем  , и накопление таких ошибок от пяти членов ряда (первые два члена – точные) будет меньше, чем
, и накопление таких ошибок от пяти членов ряда (первые два члена – точные) будет меньше, чем 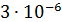 . Выпишем в отдельные столбцы результаты вычислений положительных и отрицательных членов:
. Выпишем в отдельные столбцы результаты вычислений положительных и отрицательных членов:

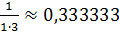

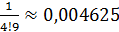







В результате вычислений получаем:
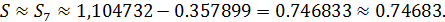
Окончательная погрешность вычислений (т.е. сумма погрешности от отбрасывания всех членов ряда, начиная с седьмого, и погрешности от неточного вычисления пяти членов ряда) меньше, чем  .
.
Итак,  и все пять цифр после запятой верные.
и все пять цифр после запятой верные.
Ряды с комплексными членами
Говорят, что последовательность комплексных чисел  сходится к числу
сходится к числу  если
если  В этом случае пишут:
В этом случае пишут:
 или
или  при
при  .
.
Координатный критерий сходимости. Если 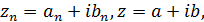 где
где  , то
, то

В силу этого критерия многие утверждения этого пособия сохраняют смысл для последовательностей и рядов комплексных чисел.
Ряд с общим членом 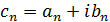 сходится тогда и только тогда, когда сходятся ряды с действительными членами
сходится тогда и только тогда, когда сходятся ряды с действительными членами  и
и  , причем в этом случае:
, причем в этом случае:
 . (3.1)
. (3.1)
Ряд (3.1) называется абсолютно сходящимся и заведомо сходится, если
сходится ряд  , членами которого являются модули членов ряда (3.1).
, членами которого являются модули членов ряда (3.1).
Пример 66. Рассмотрим геометрический ряд:
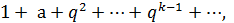 (3.2)
(3.2)
где q – комплексное число и 
Частичная сумма этого ряда 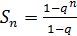 . Так как
. Так как  при
при  и
и  при
при  , то
, то  при
при  и
и  при
при  Следовательно, ряд (3.2) сходится при
Следовательно, ряд (3.2) сходится при 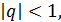 а его сумма
а его сумма 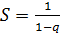 . Поэтому
. Поэтому
 . (3.3)
. (3.3)
При  ряд (3.2) расходится.
ряд (3.2) расходится.
Записав число q в виде  получаем, что
получаем, что 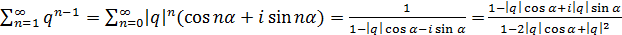 и, следовательно, для любого действительного числа
и, следовательно, для любого действительного числа 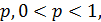 справедливы равенства:
справедливы равенства:
 ,
,
 .
.
Пример 67. Исследовать сходимость ряда  и найти его сумму.
и найти его сумму.
Так как числа  образуют геометрическую прогрессию со знаменателем
образуют геометрическую прогрессию со знаменателем  , где
, где  , то по формуле (3.3) находим:
, то по формуле (3.3) находим:

Пример 68. Исследовать сходимость ряда  . Представим общий
. Представим общий
член ряда в виде: 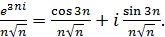 Ряды
Ряды  и
и  абсолютно сходятся, так как
абсолютно сходятся, так как

и соответственно
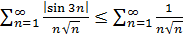 ,
,
а ряд  сходится как обобщенный гармонический. Поэтому исходный ряд абсолютно сходится.
сходится как обобщенный гармонический. Поэтому исходный ряд абсолютно сходится.
Пример 69. Исследовать сходимость ряда  .
.
Так как ряд  сходится, то и исходный ряд абсолютно сходится.
сходится, то и исходный ряд абсолютно сходится.
Пример 70. Исследовать сходимость ряда  .
.
Так как  то
то
 . Последний ряд сходится по интегральному при-знаку, так как сходится интеграл:
. Последний ряд сходится по интегральному при-знаку, так как сходится интеграл: 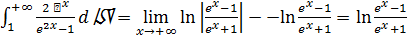 . Следовательно, исходный ряд сходится.
. Следовательно, исходный ряд сходится.
Приложения
Пример 7 1. Оценить погрешность приближенного равенства
 .
.
Погрешность этого приближенного равенства определяется суммой членов, следующих после 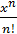 в разложении
в разложении 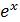 :
:

или
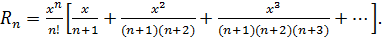
Заменив каждый из сомножителей  меньшей величиной
меньшей величиной  получим неравенство
получим неравенство

Просуммируем бесконечно убывающую геометрическую прогрессию в квадратных скобках:

Пример 7 2. Вычислить  с точностью до 0,00001.
с точностью до 0,00001.
Используя разложение 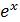 в ряд, получаем
в ряд, получаем
 .
.
Определим число n так, чтобы погрешность приближенного равенства

Не превышала 0,00001. Воспользуемся оценкой погрешности, данной в предыдущем примере. Полагаем  ; тогда
; тогда
 .
.
Путем подбора определим, при каком значении n будет выполняться неравенство  Полагая, например, n=3; получаем
Полагая, например, n=3; получаем  т.е.
т.е.  . Пусть, далее, n=5; отсюда
. Пусть, далее, n=5; отсюда  , т.е.
, т.е.  Пусть, наконец, n=6; отсюда
Пусть, наконец, n=6; отсюда  т.е.
т.е.  Итак, принимаем n=6:
Итак, принимаем n=6:
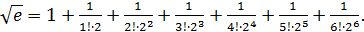
Суммируем слагаемые:

Значит,  Каждое слагаемое мы вычислили с точностью до 0,000001, чтобы при суммировании не получить погрешности, превышающей 0,00001.
Каждое слагаемое мы вычислили с точностью до 0,000001, чтобы при суммировании не получить погрешности, превышающей 0,00001.
Пример 7 3. Вычислить 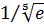 с точностью до 0,00001.
с точностью до 0,00001.
Имеем

Мы взяли 5 слагаемых, так как знакопеременный ряд удовлетворяет условиям признака Лейбница, а поэтому допускаемая погрешность по абсолютной величине должна быть меньше первого из отброшенных членов ряда. Первый из отброшенных членов равен  . Нетрудно видеть, что
. Нетрудно видеть, что  .
.
Произведя вычисления, в результате получаем 
Пример 7 4. Пользуясь разложением  в ряд, вычислить
в ряд, вычислить  с точностью до 0,0001.
с точностью до 0,0001.
Имеем

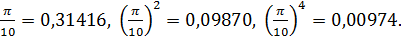
Достаточно взять три члена ряда, так как  Тогда
Тогда

Пример 7 5. Вычислить  с точностью до 0,0001.
с точностью до 0,0001.
Воспользуемся разложением 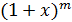 в ряд, полагая
в ряд, полагая  Имеем
Имеем
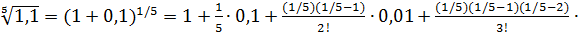

Четвертый и следующие за ним члены отбрасываем, так как четвертый член меньше 0,0001. Итак, 
Пример 7 6. Вычислить  с точностью до 0,001.
с точностью до 0,001.
Так как  является ближайшим к числу 130 кубом целого числа, то целесообразного число 130 представить в виде суммы двух слагаемых:
является ближайшим к числу 130 кубом целого числа, то целесообразного число 130 представить в виде суммы двух слагаемых: 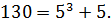 Тогда
Тогда


Четвертый член меньше 0,001 поэтому его и следующие за ним члены можно отбросить. Итак, 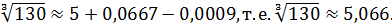
Пример 7 7 . Вычислить  точностью до 0,0001.
точностью до 0,0001.
Воспользуемся разложением  в ряд:
в ряд:

или
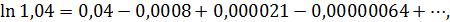
откуда 
Пример 7 8. В прямоугольном треугольнике катеты равны 1 и 5 см. Определить острый угол треугольника, лежащий против меньшего катета, с точностью до 0,001 радиана.
Так как  , то
, то  . Воспользуемся разложением
. Воспользуемся разложением

Откуда  т.е.
т.е. 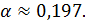
Пример 7 9. Оценить погрешность приближенного равенства

Задача сводится к оценке суммы остатка ряда

Заменив каждый из множителей  меньшим числом
меньшим числом 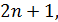 получим неравенство
получим неравенство

Просуммируем бесконечно убывающую геометрическую прогрессию в квадратных скобках:


Пример 8 0. Вычислить  с точностью до 0,0001.
с точностью до 0,0001.
В формуле для определения  и неравенстве для оценки
и неравенстве для оценки  полагаем t=1:
полагаем t=1:

Путем подбора определим n так, чтобы выполнялось неравенство  Если
Если 
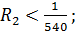 если
если  то
то  ;
; 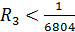 ; если
; если  то
то 

Итак,  и для вычисления
и для вычисления  получаем приближенное равенство
получаем приближенное равенство
 .
.
Суммируя эти четыре слагаемых, получим
 .
.
Пример 8 1. Вычислить  с точностью до 0,0001.
с точностью до 0,0001.
Полагаем  Тогда
Тогда
 .
.
Если  ;
;  ; если
; если 
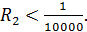 Значит, достаточно взять два члена ряда. Следовательно,
Значит, достаточно взять два члена ряда. Следовательно,
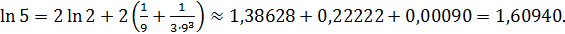
Пример 8 2. Доказать справедливость тождества  и вычислить
и вычислить  с точностью до 0,001.
с точностью до 0,001.
Полагая в равенстве


 получаем
получаем
 , или
, или  .
.
Воспользовавшись разложением  в ряд, имеем
в ряд, имеем

Выполняя вычисления, находим 
Для вычисления числа π можно было воспользоваться рядами, которые сходятся быстрее, чем только что приведенные.
Пример 8 3. Найти  .
.
Заменив 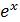 и
и  их разложениями в степенные ряды, получим
их разложениями в степенные ряды, получим

Пример 8 4. Найти  .
.
Используя разложения  и
и  в степенные ряды, имеем
в степенные ряды, имеем

Пример 8 5. Вычислить  с точностью до 0,0001.
с точностью до 0,0001.
Заменим в подынтегральном выражении  его разложением в степенной ряд, получим
его разложением в степенной ряд, получим


Пример 8 6. Вычислить  с точностью до 0,001.
с точностью до 0,001.


Пример 8 7. Вычислить  с точностью до 0,001.
с точностью до 0,001.
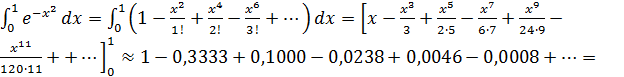
=  [2]
[2]
Заключение
На основе анализа литературы, необходимо сделать ряд выводов: Ряд — математическое выражение, позволяющее записать бесконечное количество слагаемых и подразумевающее значение их суммы, которое можно получить в предельном смысле. Если значение суммы (в предельном смысле) существует, то говорят, что ряд сходится. В противном случае говорят, что он расходится.
В ходе выполнения работы нами было рассмотрено понятие числового ряда и достаточные условия сходимости числового ряда. В данных главах мы дали характеристику определению числового ряда и сходимости, изучили основные свойства числовых рядов и их признаки. В итоге, можно заметить, что рассмотрение вопросов связанных с данной тематикой носит как теоретическую, так и практическую значимость.
Литература
1. Виноградова, И.А. Задачи и упражнения по математическому анализу [Текст]/ Виноградова, И.А., Олехник, С.Н., Садовничий, В.А. – М.: Высш. шк., 2000. – 712 с.
2. Данко, П.Е. Высшая математика в упражнениях и задачах[Текст]/ Данко, П.Е., Попов, А.Г., Кожевникова, Т.Я. – М.: Высш. шк., 1986. – 415 с.
3. Зорич, В.А. Математический анализ [Текст]/ Зорич, В.А. – М.: Наука. Гл. ред. физ.-мат. лит, 1981. – 544 с.
4. Ильин, В.А. Математический анализ [Текст]/ Ильин, В.А., Садовничий, В.А., Сендов, Б.Х. – М.: Изд-во МГУ, 1987. – 358 с.
5. Кудрявцев, Л.Д. Сборник задач по математическому анализу. Интегралы. Ряды [Текст]/ Кудрявцев, Л.Д., Кутасов, А.Д., Чехлов, В.И., Шабунин, М.И. – М.: Наука. Гл. ред. физ.-мат. лит. 1986. – 528 с.
Дата добавления: 2019-09-02; просмотров: 433; Мы поможем в написании вашей работы! |

Мы поможем в написании ваших работ!
