Комплексна форма інтеграла Фур’є
Перетворимо за допомогою формули Ейлера [2] підінтегральну функцію у формулі (2.7) до наступного вигляду
 (2.11)
(2.11)
де позначено
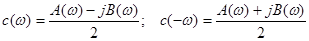
Тоді
 (2.12)
(2.12)
Для 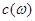 дістаємо вираз
дістаємо вираз
 (2.13)
(2.13)
Звідси
 (2.14)
(2.14)
Безпосередньо бачимо, що ці формули не втрачають сенс і при 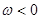 , бо
, бо  . Тому із формули (2.7) випливає
. Тому із формули (2.7) випливає
 (2.15)
(2.15)
Отже, в точках неперервності функції
 (2.16) де
(2.16) де
 (2.17)
(2.17)
Вираз для  у формі (2.15) називають комплексною формою інтеграла Фур’є для функції
у формі (2.15) називають комплексною формою інтеграла Фур’є для функції  .
.
Зауваження. Множник  можна записати у будь - яку з формул (2.16) чи (2.17): у вираз для
можна записати у будь - яку з формул (2.16) чи (2.17): у вираз для  , як у формулі (2.17), або у формулі (2.16), як це у подальшому буде зроблено для формул перетворення Фур’ є відповідно до стандартів електротехніки.
, як у формулі (2.17), або у формулі (2.16), як це у подальшому буде зроблено для формул перетворення Фур’ є відповідно до стандартів електротехніки.
Приклад. Побудувати розклад (2.17) для функції
 ,
, 
Розв‘язок
Тут  . Проінтегруємо по проміжку
. Проінтегруємо по проміжку  , відповідно (2.2) при
, відповідно (2.2) при  отримаємо
отримаємо


Оскільки
 , тоді
, тоді
 .
.
Розклад (2.18), де  запишеться як:
запишеться як:
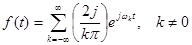
Інтегральне перетворення Фур’є
При дотриманні певних умов у ряд Фур'є розкладається періодична функція, задана на всій дійсній осі, або функція, визначена на кінцевому інтервалі. Розкладання в ряд Фур'є неперіодичної функції, заданої на необмеженому інтервалі, нездійсненно. Однак ідея подання функції нескінченним набором гармонік у декілька зміненій формі реалізована і в цьому випадку. Засобом досягнення мети служить інтеграл Фур'є [3], [4], [5].
|
|
|
Припустимо, що комплексна формула інтеграла Фур'є має місце для всіх значень  за винятком скінченої кількості точок.
за винятком скінченої кількості точок.
Тоді
 (2.18)
(2.18)
Вираз у дужках - функція від  . Позначимо цю функцію
. Позначимо цю функцію  :
:
 (2.19) тоді
(2.19) тоді
 (2.20)
(2.20)
Вирази (2.19) та (2.20) називаються двобічним прямим та оберненим перетворенням Фур'є. Якщо функція  при
при  , то дістанемо однобічні перетворення Фур'є.
, то дістанемо однобічні перетворення Фур'є.
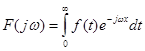 (2.21)
(2.21)
 (2.22)
(2.22)
Аналогічно, звернувшись до формул (2.9) і (2.10), можна ввести пряме і обернене косинус-перетворення Фур'є для парної функції  .
.
 (2.23)
(2.23)
 (2.24)
(2.24)
та пряме і обернене синус-перетворення Фур'є для непарної функції  :
:
 (2.25)
(2.25)
 (2.26)
(2.26)
Приклад. Знайти прямі косинус - перетворення Фур'є  та синус-перетворення
та синус-перетворення  функції
функції  .
.
 ,
, 
За формулами обернених перетворень (2.24) і (2.25) маємо


Спектральна характеристика (щільність) неперіодичної функції
У відповідності з формулою (2.22), неперіодична функція  зображується сукупністю нескінченно великої кількості гармонік з нескінченно малими амплітудами
зображується сукупністю нескінченно великої кількості гармонік з нескінченно малими амплітудами  у всьому діапазоні частот
у всьому діапазоні частот  до
до  . Функцію
. Функцію  , визначену для неперіодичної функції
, визначену для неперіодичної функції  за формулою (2.19) чи (2.22), називають спектральною характеристикою (спектральною щільністю, спектральною функцією) функції
за формулою (2.19) чи (2.22), називають спектральною характеристикою (спектральною щільністю, спектральною функцією) функції  . ЇЇ модуль
. ЇЇ модуль  і аргумент
і аргумент 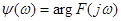 називають відповідно амплітудною та фазовою спектральними характеристиками (відповідно амплітудно-частотним та фазочастотним спектрами).
називають відповідно амплітудною та фазовою спектральними характеристиками (відповідно амплітудно-частотним та фазочастотним спектрами).
|
|
|
Деякі властивості спектральної характеристики. Нехай  - спектральна характеристика
- спектральна характеристика  (це символічно можна записати
(це символічно можна записати  . Тоді спектральній характеристиці (у випадку двобічного перетворення Фур'є) притаманні такі властивості [3]:
. Тоді спектральній характеристиці (у випадку двобічного перетворення Фур'є) притаманні такі властивості [3]:
Лінійність  де
де  ;
; 
Диференціювання оригіналу  , якщо
, якщо  абсолютно інтегрована функція. Інтегрування оригіналу
абсолютно інтегрована функція. Інтегрування оригіналу  за умови, що
за умови, що  . Диференціювання спектральної функції
. Диференціювання спектральної функції  у випадку, коли
у випадку, коли  - абсолютно інтегрована функція
- абсолютно інтегрована функція
Зміна масштабу незалежної змінної  .
. 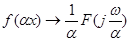
Зсув незалежної змінної  .
. 
Зсув спектральної функції 
Множення функції  на косинус та синус
на косинус та синус


Функція  - комплексно - спряжена для функції
- комплексно - спряжена для функції  , і, оскільки модулі спряжених функцій
, і, оскільки модулі спряжених функцій  і
і  рівні, а аргументи - відрізняються знаком, то амплітудно-частотний спектр - завжди парна, а фазо-частотний спектр - завжди непарна функція частоти
рівні, а аргументи - відрізняються знаком, то амплітудно-частотний спектр - завжди парна, а фазо-частотний спектр - завжди непарна функція частоти 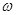 .
.
Інколи спектральну характеристику  описують кривими, що являють собою дійсну
описують кривими, що являють собою дійсну  та уявну
та уявну  частину спектральної функції.
частину спектральної функції.
|
|
|
 (3.1)
(3.1)
 (3.2)
(3.2)
Ці дві криві містять повну інформацію про амплітуду і фазу спектральної характеристики причому  - непарна функція,
- непарна функція,  - парна функція, а відтак, якщо функція
- парна функція, а відтак, якщо функція  - парна, то спектр зводиться тільки до дійсної частини
- парна, то спектр зводиться тільки до дійсної частини  , що збігається з
, що збігається з  . Аналогічно у разі непарної функції
. Аналогічно у разі непарної функції  спектр зводиться до уявної частини
спектр зводиться до уявної частини  .
.
Зауваження 1. Спектральну характеристику можна вважати обвідною коефіцієнтів ряду Фур'є, тобто границею лінійчатого спектра частот періодичної функції, коли період функції прагне до нескінченності.
Розрахункова частина
У розрахунковій частині даної роботи досліджується неперіодична функція
 ,
,
Потрібно знайти:
розклад в інтеграл Фур'є
амплітудний і фазовий спектр.
Розв'язання
а) Функція  задовольняє таким умовам теореми Фур’є [4], [5]:
задовольняє таким умовам теореми Фур’є [4], [5]:
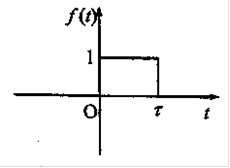
Рис.4.1 Графік досліджуємої неперіодичної функції f (t)
(прямокутний імпульс тривалості t) задана на всій осі  . на будь-якому кінцевому відрізку цієї осі задовольняє умовам Дирихле [], а отже розкладається в ряд Фур'є.
. на будь-якому кінцевому відрізку цієї осі задовольняє умовам Дирихле [], а отже розкладається в ряд Фур'є.
Абсолютно інтегрувальна по всій осі, тобто  те функція
те функція  допускає подання у формі інтеграла Фур'є
допускає подання у формі інтеграла Фур'є
 (4.1), де
(4.1), де
 (4.2)
(4.2)
Застосувавши (4.2), знайдемо спектральну щільність
|
|
|
 . (4.3)
. (4.3)
Згідно (4.1), підставляючи (4.3), отримуємо інтеграл Фур’є в комплексній формі:
 (4.4)
(4.4)
З формули (4.4) після відділення дійсної й мнимої частини можна перейти до інтеграла Фур'є в дійсній формі. З обліком парних і непарних функцій одержимо
 , тобто
, тобто
 (4.5)
(4.5)
б) Минаючи стандартну процедуру, визначимо модуль і аргумент величини  привівши її до показової форми запису
привівши її до показової форми запису
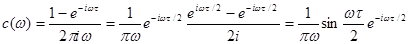 (4.6)
(4.6)
Поки співмножник експоненти (разом із синусом) міняє знак, він не може відігравати роль модуля  . Неважко перевірити, що в проміжках
. Неважко перевірити, що в проміжках
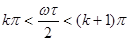 при
при 
 .
.
Тому для 
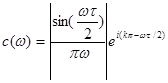 , значить
, значить  ;
;
звідки
 . (4.7)
. (4.7)
В виразі (4.7) ціле число  довільне, його варто вибрати так, щоб виділялося головне значення. Оскільки в означених вище інтервалах зміни w справедливо
довільне, його варто вибрати так, щоб виділялося головне значення. Оскільки в означених вище інтервалах зміни w справедливо  , то досить взяти
, то досить взяти  .
.
Маємо:
1. амплітудний спектр у вигляді функції
 ,
,
Побудуємо таблицю амплітудного спектра
| k | -4 | -2 | 0 | 2 | 4 |

| 
| 
| 0 | 
| 
|

| 0 | 0 | 
| 0 | 0 |
Графік амплітудного спектра наведений на рис.4.2

Рис.4.2 Графік амплітудного спектру досліджуємої неперіодичної функції
2. фазовий спектр у вигляді функції
 ,
,  . Діаграми для
. Діаграми для
 побудовані з урахуванням парності
побудовані з урахуванням парності  й непарності
й непарності  .
.
Побудуємо таблицю для фазового спектра
| k | -2 | -1 | 0 | 1 | 2 |

| 
| 
| 0 | 
| 
|
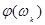
| 
| 
| 0 | 
| 
|
Графік фазового спектра наведений на рис.4.3
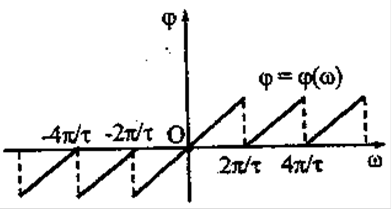
Рис.4.3 Графік фазового спектру досліджуємої неперіодичної функції
Розглянуту функцію  в радіотехніці застосовують для опису прямокутного імпульсу тривалості
в радіотехніці застосовують для опису прямокутного імпульсу тривалості  . Прилад, що реєструє цей сигнал, сприймає тільки кінцевий інтервал частот. Важливо, щоб в останній попадала основна частина спектра, який відповідає найбільшим значенням амплітуд
. Прилад, що реєструє цей сигнал, сприймає тільки кінцевий інтервал частот. Важливо, щоб в останній попадала основна частина спектра, який відповідає найбільшим значенням амплітуд  . Довжину такого інтервалу характеризують за допомогою поняття ширини спектра. У даному прикладі шириною спектра називають величину
. Довжину такого інтервалу характеризують за допомогою поняття ширини спектра. У даному прикладі шириною спектра називають величину  . Тривалість імпульсу
. Тривалість імпульсу  й ширина його спектра обернено залежні. Ця властивість - загальна для імпульсів різної форми.
й ширина його спектра обернено залежні. Ця властивість - загальна для імпульсів різної форми.
Висновки
В курсовій роботі розглянута теорія та практика спектрального аналізу функцій при спектральному представленні неперіодичних функцій з застосуванням математичного апарату інтегральних перетворень Фур’є.
Від періодичного коливання до неперіодичного можна просто перейти, якщо не змінюючи форми імпульсу безмежно збільшувати період його проходження, що, у свою чергу, приведе до нескінченно близького розташування друг до друга спектральних складових, а значення їхніх амплітуд стають нескінченно малими. Однак початкові фази цих складових такі, що сума нескінченно великої кількості гармонійних коливань нескінченно малих амплітуд відрізняється від нуля й дорівнює функції тільки там, де існує імпульс. Тому поняття спектра амплітуд для неперіодичного коливання не має змісту, і його заміняють, використовуючи пряме й зворотне перетворення Фур'є. Відомо, що функція, що задовольняє заданим умовам, може бути представлена інтегралом Фур'є (зворотне перетворення Фур'є)
 .
.
Використовуючи пряме перетворення Фур'є, приходимо до інтеграла
 .
.
Функція  називається комплексною спектральною щільністю амплітуд, а її модуль
називається комплексною спектральною щільністю амплітуд, а її модуль  - спектральною щільністю амплітуд. Аргумент
- спектральною щільністю амплітуд. Аргумент  називають фазовим спектром неперіодичного коливання.
називають фазовим спектром неперіодичного коливання.
Дата добавления: 2019-09-02; просмотров: 131; Мы поможем в написании вашей работы! |

Мы поможем в написании ваших работ!
