Некоторые термодинамические соотношения
Итак, мы получили соотношения
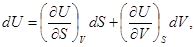 (27)
(27)
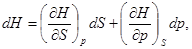 (28)
(28)
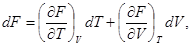 (29)
(29)
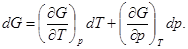 (30)
(30)
Отсюда
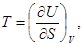
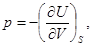 (31)
(31)
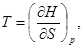
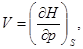 (32)
(32)
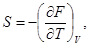
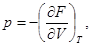 (33)
(33)
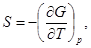
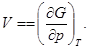 (34)
(34)
Отметим два следствия выведенных уравнений. Из определения функций F и G следует 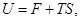
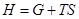 . Подставив сюда выражения для энтропии из формул (33) и (34), получим
. Подставив сюда выражения для энтропии из формул (33) и (34), получим
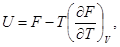 (35)
(35)
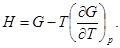 (36)
(36)
Эти уравнения называются уравнениями Гиббса — Гельмгольца. Сразу можно отметить пользу, которую можно извлечь из этих уравнений. Часто бывает легко найти свободную энергию F с точностью до слагаемого, зависящего только от температуры. Это можно сделать, вычислив изотермическую работу, совершаемую системой. Тогда формула (35) позволяет с той же неопределенностью найти и внутреннюю энергию системы.
Если известна функция 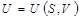 , то дифференцированием ее по S и V можно найти температуру и давление системы, т. е. получить полные сведения о ее термических свойствах. Затем по формуле
, то дифференцированием ее по S и V можно найти температуру и давление системы, т. е. получить полные сведения о ее термических свойствах. Затем по формуле 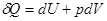 можно найти
можно найти 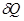 и соответствующие теплоемкости, т. е. получить полные сведения также и о калорических свойствах системы. То же самое можно сделать с помощью любого из оставшихся трех канонических уравнений состояния.
и соответствующие теплоемкости, т. е. получить полные сведения также и о калорических свойствах системы. То же самое можно сделать с помощью любого из оставшихся трех канонических уравнений состояния.
Далее, вторичным дифференцированием из соотношений (31) находим
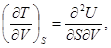
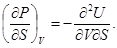
Отсюда на основании известной теоремы анализа о перемене порядка дифференцирования следует
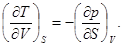 (37)
(37)
Аналогично,
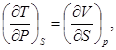 (38)
(38)
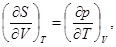 (39)
(39)
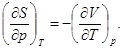 (40)
(40)
Эти и подобные им соотношения называются соотношениями взаимности или соотношениями Максвелла. Они постоянно используются для вывода различных соотношений между величинами, характеризующими термодинамически равновесные состояния системы. Такой метод вывода называется методом термодинамических функций или термодинамических потенциалов.
|
|
|
Общие критерии термодинамической устойчивости
Допустим, что адиабатически изолированная система находится в термодинамическом равновесии, причем ее энтропия S в рассматриваемом состоянии максимальна, т. е. больше энтропий всех возможных бесконечно близких состояний, в которые система может перейти без подвода или отвода тепла. Тогда можно утверждать, что самопроизвольный адиабатический переход системы во все эти состояния невозможен, т. е. система находится в устойчивом термодинамическом равновесии. Действительно, если бы такой переход был возможен, то энтропии начального 1 и конечного 2 состояний были бы связаны соотношением 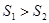 . Но это соотношение находится в противоречии с принципом возрастания энтропии, согласно которому при адиабатических переходах должно быть
. Но это соотношение находится в противоречии с принципом возрастания энтропии, согласно которому при адиабатических переходах должно быть 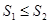 . Таким образом, мы приходим к следующему критерию термодинамической устойчивости.
. Таким образом, мы приходим к следующему критерию термодинамической устойчивости.
Если система адиабатически изолирована и ее энтропия в некотором равновесном состоянии максимальна, то это состояние являемся термодинамически устойчивым. Это значит, что система, оставаясь адиабатически изолированной, не может самопроизвольно перейти ни в какое другое состояние.
|
|
|
В приложениях термодинамики к конкретным вопросам часто бывает удобно вместо адиабатической изоляции системы накладывать на ее поведение другие ограничения. Тогда критерии термодинамической устойчивости изменятся. Особенно удобны следующие критерии.
Критерий устойчивости для системы с постоянными объемом и энтропией.
Принимая во внимание соотношение (4) и первое начало термодинамики, можно написать:
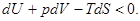 (41)
(41)
При постоянстве энтропии и объема это дает
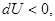 (42)
(42)
т.е. в системе могут самопроизвольно происходить лишь процессы с уменьшением внутренней энергии. Следовательно, устойчивым является состояние при минимуме внутренней энергии.
Критерий устойчивости для системы с постоянными давлением и энтропией. В этом случае условие (41) имеет вид
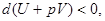 (43)
(43)
т.е. в системе могут самопроизвольно происходить лишь процессы с уменьшением энтальпии 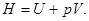 Следовательно, устойчивым является состояние при минимуме энтальпии.
Следовательно, устойчивым является состояние при минимуме энтальпии.
Критерий устойчивости для системы с постоянными объемом и температурой. При 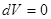 и
и 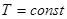 неравенство (41) записывается в виде
неравенство (41) записывается в виде
|
|
|
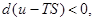 (44)
(44)
т.е. в системе могут самопроизвольно происходить лишь процессы с уменьшением свободной энергии 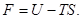 Следовательно, устойчивым является лишь состояние при минимуме свободной энергии.
Следовательно, устойчивым является лишь состояние при минимуме свободной энергии.
Критерий устойчивости для системы с постоянными температурой и давлением. С помощью выражения (17) для термодинамического потенциала неравенство (41) преобразуется к виду
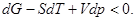 (45)
(45)
При постоянных температуре и давлении дифференциалы 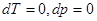 и (45) сводятся к неравенству
и (45) сводятся к неравенству
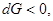 (46)
(46)
т.е. в системе могут самопроизвольно происходить лишь процессы с уменьшением термодинамического потенциала. Следовательно, устойчивым является состояние при минимуме термодинамического потенциала Гиббса.
Принцип Ле-Шателье – Брауна
Рассмотрим принцип, сформулированный французским ученым Ле-Шателье (1850—1936) в 1884 г. и, в расширенном виде, немецким физиком Брауном (185О—1918) в 1887 г. Этот принцип позволяет предвидеть направление течения процесса в системе, когда она выведена внешним воздействием из состояния устойчивого равновесия. Принцип Ле-Шателье — Брауна не является столь всеобъемлющим, как второе начало термодинамики. В частности, он не позволяет высказывать никаких количественных заключений о поведении системы. Необходимым условием применимости принципа Ле-Шателье — Брауна является наличие устойчивости равновесия, из которого система выводится внешним воздействием. Он неприменим к процессам, переводящим систему в более устойчивое состояние, например, к взрывам. Принцип Ле-Шателье — Брауна был сформулирован как обобщение знаменитого и всем хорошо известного электродинамического правила ленца (1804—1865), определяющего направление индукционного тока. Он гласит:
|
|
|
Если система находимся в устойчивом равновесии, то всякий процесс, вызванный в ней внешним воздействием или другим первичным процессом, всегда бывает направлен таким образом, что он стремится уничтожишь изменения, произведенные внешним воздействием или первичным процессом.
Ле-Шателье и Браун применяли главным образом индуктивный метод, рассмотрев большое число примеров, которые, по их мнению, являются частными случаями сформулированного ими общего правила. Данная ими формулировка была, однако, столь туманной, что не допускала в каждом конкретном случае однозначного применения правила. Неопределенность можно устранить и получить точные математические формулы, выражающие принцип Ле-Шателье —Брауна, если к рассматриваемой проблеме привлечь критерии устойчивости термодинамического равновесия, сформулированные в предыдущем параграфе.
Список использованной литературы
1. И.В. Савельев. Курс общей физики. книга 3. М.: Физматлит, 1998
2. Д.В. Сивухин. Общий курс физики. т.II. М.: Наука, 1975
3. А. К. Кикоин, И.К.Кикоин. Молекулярная физика. М.: Наука, 1976
4. А.Н. Матвеев. Молекулярная физика. М.: Высшая школа, 1981
Дата добавления: 2019-07-15; просмотров: 190; Мы поможем в написании вашей работы! |

Мы поможем в написании ваших работ!
