Оценки качества переходного процесса

Стр 1 из 2Следующая ⇒

Министерсво образования Российской Федерации

Тверской Государственный Технический Университет

Кафедра ЭВМ

«Оценка качества динамических систем при имитационном моделировании»

проф. Григорьев В.А.

Содержание

Введение................................................................................................ 3

1. Точность в установившихся режимах.............................................. 4

2. Оценки качества переходного процесса.......................................... 9

3. Корневые оценки качества.............................................................. 12

4. Интегральные критерии качества регулирования........................ 15

5. Оценки функционирования недетермированных систем [12]....... 16

6. Требования к качеству управления динамическими объектами... 18

7. Комбинированные критерии (алгоритмическая реализация) [6] 20

Литература.......................................................................................... 21

Введение

Качество работы любой системы регулирования, в конечном счете, определяется величиной ошибки, равной разности между требуемым и действительными значениями регулируемой величины: х( t )= g ( t )- y ( t ). В системах стабилизации при g ( t )=0 ошибка х( t )= - y ( t ).

Знание мгновенного значения ошибки в течении всего времени работы регулируемого объекта позволяет наиболее полно судить о свойствах системы регулирования. Однако в действительности, вследствие случайности задающего и возмущающего воздействий, такой подход не может быть реализован. Поэтому приходится оценивать качество системы регулирования по некоторым ее свойствам, проявляющимся при различных типовых воздействиях

Для определения качественных показателей системы регулирования в этом случае используются так называемые критерии качества.

В настоящее время разработано большое число различных критериев качества систем регулирования. Все их можно разбить на четыре группы

К первой группе относятся критерии, в той или иной степени использующие для оценки качества величину ошибки в различных типовых режимах. Эту группу назовем критериями точности систем регулирования .

Ко второй группе относятся критерии, определяющие величину запаса устойчивости, т.е. критерии, устанавливающие, насколько далеко от границы устойчивости находится система регулирования.

Почти всегда опасной для системы является колебательная граница устойчивости. Это связано с тем, что стремление повысить общий коэффициент усиления в системе, как правило, приводит к приближению системы именно к колебательной границе устойчивости и затем - к возникновению незатухающих автоколебаний.

Третья группа критериев качества определяет так называемое быстродействие. Под быстродействием понимается быстрота реагирования системы на появление задающих и возмущающих воздействий. Наиболее просто быстродействие может оцениваться по времени затухания переходного процесса системы.

К четвертой группе критериев качества относятся комплексные критерии, дающие оценку некоторых обобщенных свойств, которые могут учитывать точность, запас устойчивости, быстродействие.

При рассмотрении понятий запаса устойчивости и быстродействия можно исходить из двух существующих в настоящее время точек зрения.

Во-первых, можно основываться на характере протекания процессов во времени и использовать для формирования критериев качества переходную или весовую функцию, расположение полосов и нулей передаточной функции замкнутой системы (корневые методы исследования).

Во-вторых, можно основываться на некоторых частотных свойствах рассматриваемой системы, характеризующих ее поведение в установившимся режиме при действии на входе гармонического сигнала. К ним относятся полоса пропускания, относительная высота резонансного пика.

Точность в установившихся режимах

1.1 Неподвижное состояние (установившиеся состояния при постоянных значениях задающего и возмущающего воздействиях).

Критерий точности - ошибка системы. В данном случае статическая ошибка системы.

Пусть g(t)=g₀=const. Далее необходимо учесть действующие на системе возмущения. В общем случае их может быть несколько – f ₁ ( t ), f ₂ ( t ) и т.д. В неподвижном состоянии необходимо положить , l - число действующих на систему возмущений.

Далее используем изображения Карсона - Хевисойда: и т.д. Воспользуемся теоремой предельного перехода и получим установившиеся значения ошибки (статической ошибки ):

(1)

где .

Первое слагаемое в (1) – 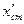– составляющая статической ошибки, определяемая задающим воздействием.

В статических системах – представляет собой общий коэффициент усиления по разомкнутой цепи и

(2)

Не следует забывать, что чувствительному элементу присущи свои ошибки и в общем случае:

где – ошибка чувствительного элемента.

При статическом регулировании . Поэтому составляющая обращается в нуль. Рассмотрим теперь ошибку регулирования .

Примем для простоты, что на систему действует одно возмущение f ₁. Тогда в статическом режиме получим:

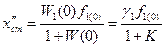, (3)

где - коэффициент статизма или отношение установившейся ошибки к постоянному возмущению.

В астатической системе . Но это еще не означает, что , т.к. возможен случай, когда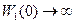

Для устранения астатическим законом регулирования от какого-либо возмущения, необходимо, чтобы интегрирующий элемент был включен в цепь регулирования до места приложения данного возмущения. Это объясняет тот факт, что повышение степени астатизма не дает возможность устранить ошибку чувствительного элемента .

1.2. Движение с постоянной скоростью

Это режим, который наблюдается в установившемся состоянии при задающем воздействии изменяющемся с постоянной скоростью: , и при постоянных значениях возмущающих воздействий 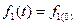; и т.д.

Используя изображения Карсона - Хевисайда, в этом случае получаем: ; ; 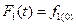и т.д.

Воспользуемся теоремой о предельном переходе и определим установившуюся ошибку в этом режиме:

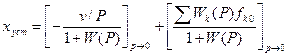(4)

Второе слагаемое этого выражения дает статическую ошибку. Первое слагаемое в (4) имеет смысл только при астатизме первого порядка:

тогда выражение (4) приводится к виду:

Таким образом, в этом режиме установившаяся ошибка будет слагаться из статической ошибки и добавочной скоростной ошибки, равной отношению скорости задания к добротности системы по скорости:

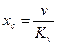
Так как система может двигаться с различными скоростями, то качество ее удобнее характеризовать не самой скоростной ошибкой «которая является переменной величиной, а значением добротности по скорости:

В статических системах первое слагаемое (4) стремится к бесконечности; при астатизме выше первого порядка это слагаемое стремится к нулю. Поэтому режим движения с постоянной скоростью используется для оценки точности только систем с астатизмом первого порядка (следящих систем).

1.3. Движение с постоянным ускорением

В этом случае задающее воздействие меняется по закону

Возцущаюкиз воздействия принимаются постоянными. Этот режим имеет смысл только в следящих системах и системах программного регулирования.

Аналогично изложенному выше, установившиеся значения ошибки в этом режиме может быть найдено из выражения

(5)

Второе слагаемое (5) дает статическую ошибку. Первое слагаемое (5) имеет смысл только при астатизме второго порядка.

Тогда выражение (5) приводится к виду

Качество системы может быть оценено величиной добротности по ускорению:

Этот типовой режим используется только для систем регулирования с астатизмом второго порядка.

1.4. Движение по гармоническому закону

Этот режим используется весьма часто, так как он позволяет наиболее полно полно оценить динамические свойства системы регулирования. Задающее воздействие принимается изменяющимся по закону .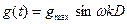

В зависимости от конкретного вида системы регулирования возмущающие воздействия в рассматриваемом режиме могут оставаться постоянным или меняться. Случай постоянства возмущений приводит к появлению некоторой постоянной ошибки x _ст .

Более вероятным является случай, когда возмущающие воздействия при движении системы в этом режиме меняются во времени. Этот случай довольно сложен, и он может рассматриваться только в приложении к конкретным системам регулирования. Рассмотрим ошибку, определяемую только первым слагаемым выражения

(6)

В линеаризованной системе, при гармоническом задающем воздействии, ошибка в установившемся режиме будет также меняться по гармоническому закону с частотой .

(7)

Точность системы в этом режиме может быть оценена по амплитуде ошибки, которая может быть найдена из (6) на основании символического метода подстановкой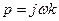

(8)

Так как предполагается, что амплитуда ошибки значительно меньше амплитуды входного воздействия: x_max << g_max, следовательно модуль знаменателя (8) намного больше единицы.

Это позволяет с большой точностью выражение (8) заменить приближенным:

(9)

где 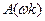- модуль частотной передаточной фикции разомкнутой системы при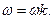

Полученная формула (9) широко используется при расчете систем методом Л.А.X.:

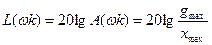(10)

1.5. Коэффициенты ошибок

Метод может применяться для задающего g ( t ), так и для возмущающего воздействия f ( t ). Не снижая общности рассуждений, рассмотрим случай, когда имеется только задающее воздействие.

Если g ( t ) имеет произвольную форму, но достаточно плавную вдали от начальной точки процесса в том смысле, что через некоторое время существенное значение имеет только конечное число т производных

то ошибка системы определяется следующим образом:

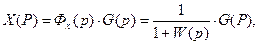(11)

где - передаточная функция замкнутой системы по ошибке, G(p) - изображение задающего воздействия.

Разложим передаточную функцию по ошибке в ряд по возрастающим степеням комплексной величины р:

, (12)

сходящейся при малых значениях р (или при достаточно больших значениях ?), что соответствует установившемуся процессу изменения регулируемой величины при заданной форме управляющего воздействия.

Переходя в выражении (12) к оригиналу, получаем формулу для установившейся ошибки:

(13)

Величины с₀, с₁, с₂ ... - называются коэффициентами ошибок. Они определяются по общему правилу разложения функции в ряд Тейлора:

В системах со статической ошибкой .

В системах с астатизмом первого порядк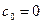а: ; а .

В системах с астатизмом второго порядка:

Оценки качества переходного процесса

Оценку качества переходного процесса (оценку запаса устойчивости и быстродействия) можно произвести по виду кривой переходного процесса при некотором типовом входном воздействии, которым может быть как задающее, так и возмущающее воздействие. В качестве типового входного воздействия обычно рассматривается единичный скачок. В этом случае кривая переходного процесса - переходная характеристика системы. Она может строится для регулируемой величины y(t) или для ошибки x(t).

1. Перерегулировани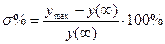е: , где .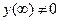

Характеризует склонность системы к колебаниям. В большинстве случаев считается, что запас достаточен, если .

2. Статическая погрешность регулирования равна отклонению регулируемой величины в новом положении равновесия от ее значения в исходном состоянии равновесия.

На рис. 1а 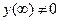, на рис. 1б - ; .

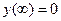3. Динамическая погрешность регулирования y _дин представляет собой максимальное отклонение регулируемой величины в переходном процессе от заданного значения. (пpи 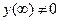, совпадает с величиной перерегулирования ).

4. Быстродействие системы определяется по длительности переходного процесса t_n. Длительность переходного процесса определяется как время, протекающее от момента подачи единичного скачка до момента, после которого имеет место неравенство:

где - обычная допустимая ошибка; величины скачка на входе.

5. Число колебаний - N_k . Показатель характеризует соотношение степени колебательности и степени затухания процесса.

6. Время запаздывания t _з, равное отрезку времени, заключенному между моментом приложения входного скачкообразного сигнала и моментом времени, при котором осредненная выходная величина становится равной половине ее установившегося значения (в случае, если на передний фронт сигнала накладываются высокочастотные колебания).

7. Время нарастания t _н, равное отрезку времени, заключенному между точкой пересечения оси времени с касательной, проведенной к осредненной кривой переходной характеристики в точке t = t _з , и координатой t точки пересечения указанной касательной с горизонтальной прямой, соответствующей установившемуся значению регулируемой величины. Максимальное время нарастания ограничивается требуемым быстродействием. Минимальное время нарастания ограничивается допустимыми в системе ускорениями и колебательными режимами.

8. Верхняя (мажорента) и нижняя (минорента) границы области допустимых значений, при которых [5].

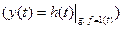9. Начальное значение .

10. Перерегулирование с учетом начальных условий H_max% - относительная величина максимального выброса y _дин переходной характеристики:

11. Время установления - t _у - время достижения переходной характеристикой первого максимума.

12. Частота колебаний f_k :

, где Т _k - "период" колебаний.

Связь с числом колебаний

(см. рис 3).

Рис 3.

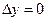13. Величина перехода – – отношение абсолютной величины максимального отклонения отрицательного энака y ₂ (относительно состояния равновесия) к максимальному отклонению положительного знака y ₁(см. рис 3). Часто принимают , либо [6]

14. Собственная частота колебаний в системе [7]

, где А _i - амплитуда i-го колебания, S_i - площадь i-й полуволны.

15. Косвенный коэффициент

Корневые оценки качества

Вид корней характеристического уравнения определяет характер переходных процессов в CAP.

Поэтому можно сформулировать требования по закону устойчивости и быстродействию системы, не рассматривая самих переходных процессов.

1. Величина среднегеометрического корня [6].

Пусть характеристическое уравнение системы имеет вид

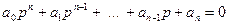(1)

Величина среднегеометрического корня равна:

где - корни характеристического уравнения. Исходное характеристическое уравнение примет вид:

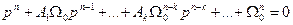, (2)

Среднегеометрический корень 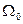может служить мерой быстроты протекания переходных процессов. Если в уравнении (2) увеличить 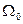, например, в 10 раз, то на основании теории подобия (табл. 7.2 в [6] оригинал f(at) соответствует и 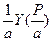где F(р) и Y(р) - изображения соответственно по Лапласу и Карсону - Хевисайду).

Примечание: от уравнения (1) путем подстановки 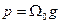можно перейти к (3)

, (3)

а его корни , .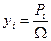

В связи с этим можно рассматривать (3) как некоторое нормированное характеристическое уравнение, которому соответствует переходной процесс, построенный для безразмерного времени . Если качество переходного процесса является приемлемым с точки зрения допустимого запаса устойчивости, определяемого, например, перерегулированием, то требуемая быстрота и протекание переходного процесса может быть обеспечена соответствующим выбором величины .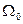

Для увеличения величины 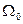необходимо увеличивать свободный член характеристического уравнения . В статических системах , в астатических , где К - общий коэффициент усиления разомкнутой цепи регулирования.

2. Степень устойчивости h (его следовало бы заменить степенью быстродействия [6])

Степень устойчивости процесса h [1,2,3] характеризует интенсивность его (процесса) затухание и численно равна абсолютному значению действительной части корня характеристического уравнения с наименьшей действительной частью.

Здесь может быть два случая [6]

- ближайший корень является вещественным (к оси мнимых чисел). Составляющая в переходном процессе, определяемая этим корнем, будет иметь вид: . Положив в конце переходного процесса , можно получить зависимость между степенью устойчивости и временем переходного процесса:

. (4)

Если принять , то

- ближайшей к оси мнимых является пара комплексных корней - . Составляющая в переходном процессе, определяемая этой парой комплексных чисел будет равна: . Положив нельзя в общем виде определить время переходного процесса. Однако можем найти верхнюю границу переходного процесса, положив . Получим:

(5)

3. Степень колебательности процесса m [1,2,3]:

Характеризует затухание его колебательных составляющих и численно равна абсолютному значению отношения действительной части к коэффициенту при мнимой части корня характеристического уравнения к наименьшим абсолютным значениям этого отношения

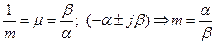В разных источниках под степенью колебательности принимают то m [1,2,3], то [6].

4. Как известно, для оценки колебательности составляющих процессов имеются и иные критерии. Например, часто затухание характеризуют логарифмическим коэффициентом колебаний:

(логарифмический декремент затухания)

где y_n и y_n ₊₁ – n-ная и (n+1)-я амплитуды рассматриваемой колебательной составляюще. Подставив в эту формулу значения y_n и y_n ₊₁ получим, что

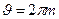, откуда:

5. Очень удобной с практической точки зрения оценкой является также степень затухания колебательной составляющей:

где y_n и y_n₊₂ – n-я и (n+2)-я амплитуды рассматриваемой составляющей. Легко установить, что

m	0	0,141	0,221	0,366	0,478	1,00	¥
y	0	0,600	0,750	0,900	0,980	0,988	1,0

Замечание: Комплексные сопряженные корни дают в выражении переходного процесса член вида: . Найдем затухание амплитуды синусоидального колебания за один период.

При некотором : . Через один период :

Отсюда определяется выражение: . Обычно в CAP допускается затухание за период не менее чем 90¸98%.

Дата добавления: 2019-07-17; просмотров: 462; Мы поможем в написании вашей работы!

Поделиться с друзьями:

12 Следующая ⇒

Мы поможем в написании ваших работ!