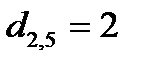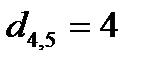ИССЛЕДОВАНИЕ ЭФФЕКТИВНОСТИ АЛГОРИТМОВ
ТРАССИРОВКИ ПРОВОДНЫХ СОЕДИНЕНИЙ
Цель работы – исследовать эффективность алгоритмов трассировки проводных соединений методом «внавал»; освоить особенности алгоритмизации и программирования задачи трассировки проводов на ПЭВМ; приобрести навыки построения математических моделей проводных соединений, реализации и исследования их при решении задачи трассировки с применением САПР.
АЛГОРИТМЫ ТРАССИРОВКИ ПРОВОДОВ
Задача проектирования соединений, иначе трассировка соединений, возникает на последних этапах проектирования радиоэлектронных средств (РЭС) и является одной из наиболее сложных задач в общей проблеме автоматизации проектирования РЭС [1-5]. Связано это с многообразием способов конструкторско-технологической реализации соединений, каждый из которых обусловливает использование специфических критериев оптимизации и ограничений при алгоритмическом решении этой задачи.
Проводной монтаж, несмотря на широкое применение печатного монтажа, занимает значительное место в современных РЭС. Он более прост, т. к. проводники изолированы друг от друга, не надо думать об ограничениях на пересечения проводов, поэтому достаточно минимизировать длину соединений. В серийном производстве проводные соединения используют в узлах, платах, субблоках, кассетах, блоках, рамах, шкафах.
В современных РЭС трассировку проводных соединений производят двумя способами [1-2]:
|
|
|
– по прямым, соединяющим отдельные выводы модулей (монтаж «внавал»);
– по ортогональным направлениям – с помощью жгутов.
Математическая формулировка задачи
В общем виде задача формулируется следующим образом [2]. В системе координат XYZ, связанной с коммутационным пространством модуля, задано местоположение множества выводов  . Это множество M разобьем в соответствии с электрической схемой соединений на непере-секающиеся подмножества M(1), M(2),…,M(k), каждое из которых включает в себя выводы, подлежащие электрическому объединению. Для каждого подмножества
. Это множество M разобьем в соответствии с электрической схемой соединений на непере-секающиеся подмножества M(1), M(2),…,M(k), каждое из которых включает в себя выводы, подлежащие электрическому объединению. Для каждого подмножества  , i = 1, 2, …, k требуется определить последовательность соединений выводов и конфигурацию проводников, обеспечивающих при заданных ограничениях минимальную суммарную длину соединений.
, i = 1, 2, …, k требуется определить последовательность соединений выводов и конфигурацию проводников, обеспечивающих при заданных ограничениях минимальную суммарную длину соединений.
Практически задача сводится к отысканию дерева с минимальной суммарной длиной ребер (построению кратчайшей связывающей сети). Согласно теореме Кэли на n вершинах может быть построено t = n ( n -2) деревьев. Поэтому при большом числе выводов в электрической цепи эта задача становится сложной.
Для определения минимального дерева на заданных n вершинах можно построить все возможные деревья и выбрать минимальное из них. Однако в РЭC число цепей исчисляется сотнями, поэтому поиск всех деревьев практически нереален. К тому же существующие алгоритмы построения минимальных деревьев позволяют находить глобально-оптимальные или близкие к ним решения (при отсутствии ограничений на количество проводников, подсоединяемых к одному выводу). Поэтому эта задача является одной из немногих задач теории графов, которые считают полностью решенными . Рассмотрим используемые в САПР алгоритмы Дж. Краскала и Р. К. Прима.
|
|
|
АЛГОРИТМ Дж.КРАСКАЛА
1. На множестве вершин (выводов) M построить взвешенный полный граф (число ребер в нем n ( n -1)/2 ). Для этого вычислить элементы матрицы расстояний  по одной из формул:
по одной из формул:
 или (5.1)
или (5.1)
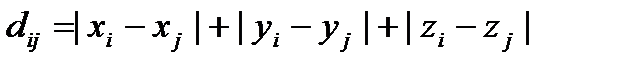 , (5.2)
, (5.2)
где  и
и  – координаты i-й и j-й позиций монтажного пространства.
– координаты i-й и j-й позиций монтажного пространства.
Формулой (5.1) пользуются для монтажа «внавал», а формулой (5.2) – при жгутовом монтаже.
2. Всем элементам, лежащим на главной диагонали и ниже её, присваивается значение  . Присвоить нулевое значение длине L рёбер искомого дерева: L = 0; i = 0; j = 0.
. Присвоить нулевое значение длине L рёбер искомого дерева: L = 0; i = 0; j = 0.
3. Сформировать таблицу меток и локальных степеней вершин:  ;
;  ;
;  ;
;  ;
;  .
.
4. Присвоить 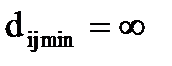 .
.
5. Найти минимальный элемент  матрицы
матрицы  .
.
|
|
|
6. Если 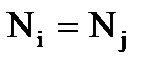 , то идти к 4.
, то идти к 4.
7. Если  или
или  , то идти к 4.
, то идти к 4.
8. Поглощение меток: все метки нового фрагмента получают значение  , а локальные степени соединенных вершин –
, а локальные степени соединенных вершин –  и
и  .
.
9. Включить ребро  во множество R ребер минимального дерева, а длину дерева увеличить на длину ребра:
во множество R ребер минимального дерева, а длину дерева увеличить на длину ребра:  .
.
10. Если  , то идти к 4, в противном случае к 11.
, то идти к 4, в противном случае к 11.
11. Минимальное дерево построено. R – множество его ребер, а L – суммарная их длина.
Конец.
Ручной расчет.
Составляем матрицу длин и всем элементам, лежащим на главной диагонали и ниже нее, присваиваем значение  :
:
1 2 3 4 5 6 7 8 9 10
1 ∞ 5 2 3 6 10 10 13 15 17
2 ∞ 4 3 2 6 6 9 11 13
3 ∞ 2 5 9 9 12 14 16
4 ∞ 4 8 8 11 13 15
5 ∞ 5 5 8 10 12
6 ∞ 1 4 6 8
7 ∞ 4 6 8
8 ∞ 3 5
9 ∞ 2
10 ∞
Формируем таблицу меток и локальных степеней. Табл. 1
На нулевом шаге все вершины получают метки, равные их номерам  , а локальные степени
, а локальные степени 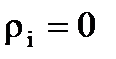 ,
,  , длина строящегося дерева
, длина строящегося дерева  и множество ребер в дереве
и множество ребер в дереве
êR ê = Æ .
| Номер вершины | Значения меток
| |||||||||||||||||||||
| 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | |||||||||||||

| 
| 
| 
| 
| 
| 
| 
| 
| 
| 
| 
| 
| 
| 
| 
| 
| 
| 
| 
| |||
| 1 | 1 | 0 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 |
|
|
|
| 1 | 1 | ||||||
| 2 | 2 | 0 | 2 | 0 | 2 | 1 | 2 | 1 | 2 | 1 | 2 | 1 | ||||||||||
| 3 | 3 | 0 | 1 | 1 | 1 | 1 | 3 | 1 | 3 | 1 | 3 | 1 | ||||||||||
| 4 | 4 | 0 | 4 | 0 | 4 | 0 | 3 | 1 | 3 | 1 | 3 | 1 | ||||||||||
| 5 | 5 | 0 | 5 | 0 | 2 | 1 | 2 | 1 | 2 | 1 | 5 | 1 | ||||||||||
| 6 7 8 9 10 | 6 7 8 9 10 | 0 0 0 0 0 | 6 7 8 9 10 | 0 0 0 0 0 | 6 7 8 9 10 | 0 0 0 0 0 | 6 7 8 9 10 | 0 0 0 0 0 | 6 7 8 8 10 | 0 0 1 1 0 | 5 7 8 8 10 | 1 1 1 1 0 | ||||||||||

| 0 |
|
|
|
|
|
|
|
|
| ||||||||||||

| 0 | 2 | 4 | 6 | 9 | 11 | 14 | 18 | 22 | 27 | ||||||||||||

| 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | ||||||||||||
Помечаем элемент  и на его место записываем
и на его место записываем  . Соединяем вершину 2-ю и 3-ю ребром: метки у них становятся равными:
. Соединяем вершину 2-ю и 3-ю ребром: метки у них становятся равными:  . Локальные степени обеих вершин равны единицам –
. Локальные степени обеих вершин равны единицам –  и
и  . Делаем несколько аналогичных шагов по выбору минимального элемента. Получаем матрицу
. Делаем несколько аналогичных шагов по выбору минимального элемента. Получаем матрицу
1 2 3 4 5 6 7 8 9 10
1 ∞ 5 ∞ [3] 6 10 10 13 15 17
2 ∞ ∞ [3] ∞ 6 6 9 11 13
3 ∞ ∞ [5] 9 9 12 14 16
4 ∞ ∞ 8 8 11 13 15
5 ∞ ∞ 5 8 10 12
6 ∞ ∞ 4 6 8
7 ∞ ∞ 6 8
8 ∞ ∞ 5
9 ∞ ∞
10 ∞
Проделываем шаги. Строим дерево
1 2 8
7 9
3
6 10
4 5
Сравним полученные результаты с результатами прикладной программы САПР.
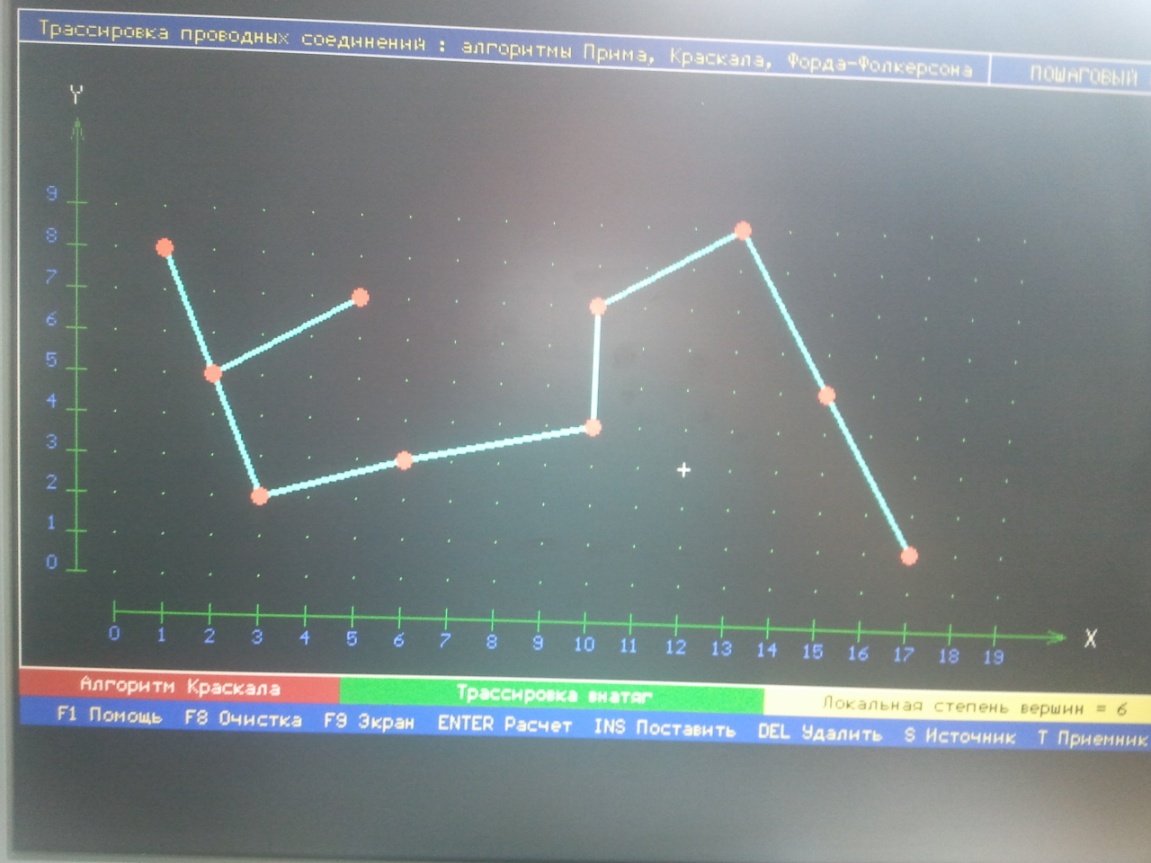
Рис. 9 Агоритм Краскала.
Алгоритм Прима
Алгоритм Прима реализует следующую процедуру [1 – 7].
На каждом шаге просматриваются только те ребра графа, которые связы-вают вершины строящегося поддерева с новыми, еще не присоединенными вершинами, т.е. ищется вершина, ближайшая от всего построенного фрагмента дерева. Отсюда, в отличие от алгоритма Краскала, единственное строящееся поддерево последовательно наращивается до построения остова.
Основные принципы построения минимального связывающего дерева (или кратчайшей связывающей сети) при наличии ограничений на локальные степени вершин  следующие.
следующие.
В начале любая произвольная вершина  соединяется с ближайшей соседней, образуя исходное поддерево. (Для определенности построения мини-мального дерева можно начинать с ребра, инцидентного первой вершине
соединяется с ближайшей соседней, образуя исходное поддерево. (Для определенности построения мини-мального дерева можно начинать с ребра, инцидентного первой вершине 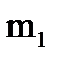 , или с минимального ребра). На каждом последующем шаге к строящемуся поддереву присоединяют очередное ребро минимально возможной длины, связывающее новую, еще не присоединенную вершину
, или с минимального ребра). На каждом последующем шаге к строящемуся поддереву присоединяют очередное ребро минимально возможной длины, связывающее новую, еще не присоединенную вершину  с одной из вершин поддеревьев
с одной из вершин поддеревьев  , локальная степень которой
, локальная степень которой 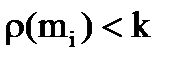 .
.
Для реализации алгоритма составляют матрицу расстояний  , элемент
, элемент  которой вычисляют по одной из формул (5.1) или (5.2). Просматривают элементы первой строки матрицы D и находят минимальный элемент. Пусть таким оказался элемент g-го столбца, тогда весь 1-й и g-й столбцы матрицы D исключаются из рассмотрения, а первое соединение проводится между точками
которой вычисляют по одной из формул (5.1) или (5.2). Просматривают элементы первой строки матрицы D и находят минимальный элемент. Пусть таким оказался элемент g-го столбца, тогда весь 1-й и g-й столбцы матрицы D исключаются из рассмотрения, а первое соединение проводится между точками 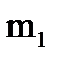 и
и  . Просматриваются 1-я и g-я строки матрицы с оставшимися элементами. Из элементов этих строк находится минимальный. Предположим, что им оказался элемент, принадлежащий j-му столбцу. Если этот элемент находится на пересечении с первой строкой, то точку
. Просматриваются 1-я и g-я строки матрицы с оставшимися элементами. Из элементов этих строк находится минимальный. Предположим, что им оказался элемент, принадлежащий j-му столбцу. Если этот элемент находится на пересечении с первой строкой, то точку  соединяем с 1-й точкой (
соединяем с 1-й точкой ( 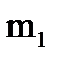 ), если же он находится на пересечении с g-й строкой, то точку
), если же он находится на пересечении с g-й строкой, то точку  соединяем с g-й (
соединяем с g-й (  ), после чего из матрицы D исключаем все элементы j-го столбца. Просматриваются 1-я, g-я и j-я строки и т. д.
), после чего из матрицы D исключаем все элементы j-го столбца. Просматриваются 1-я, g-я и j-я строки и т. д.
Выполнение ограничения на локальную степень  вершин обеспе-чивается проверкой в каждой просматриваемой i-ой строке числа уже выбранных для построения минимального дерева элементов –
вершин обеспе-чивается проверкой в каждой просматриваемой i-ой строке числа уже выбранных для построения минимального дерева элементов –  . При
. При  все оставшиеся элементы i-й строки исключаются из рассмотрения, т.е. эта строка удаляется.
все оставшиеся элементы i-й строки исключаются из рассмотрения, т.е. эта строка удаляется.
АЛГОРИТМ
1. Вычислить элементы матрицы расстояний  по одной из формул – (5.1) или (5.2).
по одной из формул – (5.1) или (5.2).
2. Найти минимальный элемент матрицы  , где
, где  ;
;  . Номера строки и столбца q и p, на пересечении которых он находится, определяют номера вершин
. Номера строки и столбца q и p, на пересечении которых он находится, определяют номера вершин  и
и  , соединяемых ребром.
, соединяемых ребром.
3. Занести номера вершин во множество  , построенное ребро – во множество
, построенное ребро – во множество  .
.
4. Подсчитать локальные степени 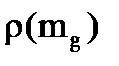 и
и  , подлежащих соединению на данном шаге вершин
, подлежащих соединению на данном шаге вершин  и
и  .
.
5. Проверить условие  и
и  . Индексы вершин, для которых это условие не выполняется, указывают номера строк матрицы D, которые необходимо исключить из рассмотрения.
. Индексы вершин, для которых это условие не выполняется, указывают номера строк матрицы D, которые необходимо исключить из рассмотрения.
6. Найти  . Здесь
. Здесь  ,
,  , т. е. среди еще не вошедших в дерево вершин отыскать вершину
, т. е. среди еще не вошедших в дерево вершин отыскать вершину  , минимально удаленную от некоторой вершины дерева
, минимально удаленную от некоторой вершины дерева  .
.
7. Дополнить множества  ;
;  .
.
8. Проверить, все ли вершины графа соединены ветвями  . Если условие выполняется, идти к 9, иначе – к 4.
. Если условие выполняется, идти к 9, иначе – к 4.
Конец.
Ручной расчет. Матрица расстояний D
1 2 3 4 5 6 7 8 9 10
1 0 5 2 3 6 10 10 13 15 17
2 5 0 4 3 2 6 6 9 11 13
3 2 4 0 2 5 9 9 12 14 16
4 3 3 2 0 4 8 8 11 13 15
5 6 2 5 4 0 5 5 8 10 12
6 10 6 9 8 5 0 1 4 6 8
7 10 6 9 8 5 1 0 4 6 8
8 13 9 12 11 8 4 4 0 3 5
9 15 11 14 13 10 6 6 3 0 2
10 17 13 16 15 12 18 9 5 2 0
Просматриваем все строки матрицы и выбираем элемент, являющийся минимальным. выбираем элемент с наименьшими индексами . Помечаем его, локальные степени вершин увеличиваем на единицу . Исключаем из рассмотрения (вычеркиваем) все элементы этих столбцов. Соединяем  и
и  соединяем 1,3
соединяем 1,3
Преобразовываем получаем матрицу D1
1 2 5 8 9 10
2 5 0 2 9 11 13
4 3 3 4 11 13 5
5 6 2 0 8 10 12
6 10 6 5 4 6 8
7 10 6 5 4 6 8
8 13 9 8 0 3 5
9 15 11 10 3 0 2
10 17 13 12 5 2 0
Снова преобразовываем
2 5 8 9 10
2 0 2 9 11 13
4 3 4 11 13 5
5 2 0 8 10 12
6 6 5 4 6 8
7 6 5 4 6 8
8 9 8 0 3 5
9 11 10 3 0 2
10 13 12 5 2 0
Продолжаем преобразование до соединения всех вершин.
в результате преобразований определяем вершины для соединения
d=1,3 d= 2,3 d=3,4 d=7,6 d=9,10 и.тд
1 8
2 7 9
3
10
4 5 6
Сравним результаты с результатами полученными прикладной программой САПР
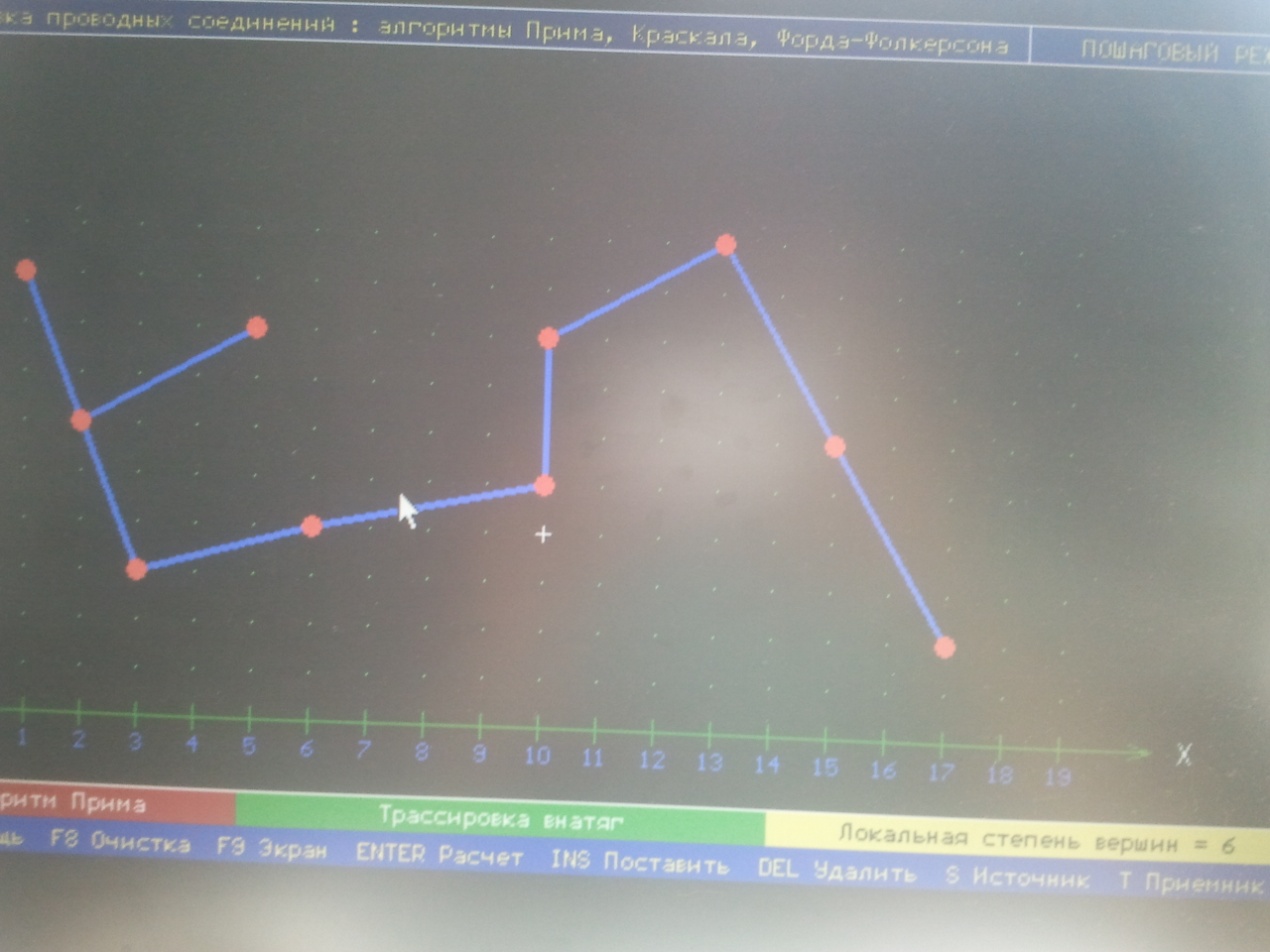
Рис. 10 Алгоритм Прима.
Дата добавления: 2019-07-17; просмотров: 302; Мы поможем в написании вашей работы! |

Мы поможем в написании ваших работ!

 вершин на очередном шаге
вершин на очередном шаге