Зміна опору в ланцюзі з індуктивністю

⇐ ПредыдущаяСтр 2 из 5Следующая ⇒

При включенні котушки індуктивності, що має параметри R і L, опір ланцюга зменшується стрибком від ∞ до R, а при виключенні воно збільшується від R до ∞. Відповідно до таких змін опору струм в ланцюзі за час перехідного періоду збільшується від 0 до I або зменшується від I до 0.

При стрибкоподібній зміні опору ланцюга в кінцевих межах теж виникає перехідний процес, який у загальних рисах подібний вже розглянутим процесам.

Другий закон комутації застосовується до ланцюгів, що містять ємність:

u (t = - 0) =u (t = + 0),

тобто, напруга на ємності не може змінитися стрибком; напруга на ємності в перший момент перехідного періоду (при t = + 0) залишається такою, яким вона була в останню мить попереднього сталого режиму(при t = - 0).

Електричний стан ланцюга (рис.1.5) у будь-який момент перехідного періоду характеризується рівнянням, складеним за другим законом Кірхгофа:

U = U _с + U _R = u_c + iR = U _с+ i C(du_c/dt).

Процес заряду конденсатора

Аналіз процесу зарядки конденсатора від джерела постійної напруги багато в чому співпадає з аналізом перехідного процесу після включення котушки на постійну напругу, оскільки рівняння електричного стану є аналогічними.

Графіки залежності напруги на конденсаторі u_C і зарядного струму i_з від часу зображені на рис.1.6.

Постійна часу ланцюга (τ = RC) є показником тривалості перехідного процесу і залежить від параметрів ланцюга R і С.

Конденсатор знаходиться під дією вимушеної і вільної складових напруги

u_С = u_{С пр} + u_{С cв} = U + ,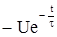

а зарядний струм складається тільки з вільної складової

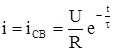оскільки а вимушена складова відсутня: i_пр = i_у = 0.

Вплив величини напруги джерела і параметрів ланцюга

Перехідний процес при зарядці конденсатора від джерела постійної напруги характеризують три показники: стала напруга на конденсаторі, початкова швидкість зміни напруги, постійна часу; при зміні напруги джерела змінюються стала напруга на конденсаторі і початкова швидкість зміни напруги, а постійна часу ланцюга від напруги не залежить. На рис.1.7 приведені (відповідно двом різним напругам джерела U₁ і U₂) графіки зміни напруги на конденсаторі.

Зміна ємності впливає на тривалість перехідного процесу так само, як зміна опору (рис.1.9).

Перехідний процес при розряді конденсатора

Після перемикання перемикача конденсатор не може розрядитися миттєво, тобто напруга u_C не може зменшитися стрибком до нуля, а підтримується протягом перехідного періоду за рахунок енергії, накопиченої в електричному полі конденсатора; при цьому в активному опорі R здійснюється необоротний процес перетворення електричної енергії в теплову..

Напруга на конденсаторі при розрядці виражається рівнянням

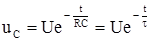де..τ = RC – постійна часу ланцюга.

Тривалість перехідного процесу, як і при зарядці, теоретично рівна нескінченності, а практично розрядка вважається закінченою при t = (4÷5) τ.

Використовуючи різні варіанти з'єднання активного опору R і реактивних компонентів (L і C) будуються диференціюючи і інтегруючі ланцюги, які знаходять широке застосування для формування різного роду імпульсних сигналів у вимірювальній, цифровій і біомедичній апаратурі.

Диференціюючи ланцюги

Диференціюючими звуться електричні ланцюги, в якому вихідна величина пропорційна похідною від вхідної величини. Простими ланцюгами що диференціюють можуть служити ланцюги, до складу яких входить резистор з конденсатором, або резистор з котушкою індуктивності.

У ланцюгу, до складу яких входить резистор з конденсатором

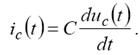
Приймаючи u_c(t) за вхідну величину, а струм i_c(t) - за вихідну, одержимо ланцюг що диференціює.

У ланцюгу, до складу яких входить резистор з котушкою індуктивності

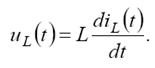
Приймаючи i_L(t) за вхідну величину, а u_L(t) - за вихідну, одержимо ланцюг що диференціює.

Використовувати струм як вхідну або вихідну величину практично скрутно, оскільки в першому випадку необхідно мати стабільне джерело струму, а в другому для його вимірювання необхідно включити послідовно додатковий опір, який робить вплив на перехідній процес в ланцюзі. Отже, вхідною і вихідною величинами доцільно вибирати напруги, при цьому використовуються rC-и rL-ланцюги

На практиці широкого поширення набув rC-ланцюг.

Умова, при якій rC-ланцюг виконує операцію диференціювання, витікає з рівняння

u₁(t) = u_с(t) + u_r(t).

Якщо прийняти

u_r(t) << u_с(t),

то

u_с(t) ≈ u₁(t).

При не синусоїдальній формі напруги u_1(t)умова диференціювання повинна бути виконана для всіх гармонійних складових вхідного сигналу. При цьому умовою диференціювання є

де ωВ – частота найвищої гармоніки, якої не можна нехтувати.

Наприклад, крива напруги прямокутної форми визначається за допомогою ряду

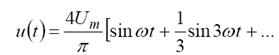
Найвищою розрахунковою частотою звичайно вважають частоту 11-й гармоніки. Тому

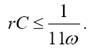
Ідеальне диференціювання прямокутного імпульсу показане на рис.1.12 а, и б. Амплітуда вихідного сигналу u2(t) нескінченно велика.

Графік напруги u_2(t)на вході та виході реального ланцюга що диференціює показаний рис. 1.13.

Рисунок 1.13 – Графік напруги реального ланцюга що диференціює

Напруга u2(t) є імпульсами експоненціальної форми з полярністю, що чергується. За тривалість вихідного імпульсу приймають час, рівний потрійному значенню постійного часу ланцюга tu вих ≈ 3τ. Амплітуда імпульсів рівна величині вхідної напруги.

Порівняння тимчасових діаграм реального і ідеального ланцюга що диференціює показує, що при зменшенні τ тривалість імпульсів u2(t) скорочується і крива u2(t) прагне формою до похідної вхідної напруги. Диференціюючи ланцюги називаються також, ланцюгами що укорочують, оскільки тривалість вихідних імпульсів значно менша, ніж вхідних.

Інтегруючи ланцюги

Інтегруючим називається електричний ланцюг, в якому вихідна величина пропорційна інтегралу від вхідної величини (мал. 1.14). Широке застосування на практиці одержав інтегруючий rC-ланцюг.

Напруга на виході ланцюга

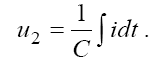
Якщо напруга на конденсаторі складає малу частину від напруги на опорі, то струм i(t) в ланцюзі буде пропорційний вхідній напрузі:

отже,

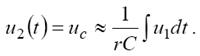
Отже, при виконанні умови

u_c << u_r або u₁ ≈ u_r

ланцюг rC є інтегруючим.

При не синусоїдальному сигналі умова повинна виконуватися для гармонійної складової найменшої частоти ω_H, тобто частоти повторення вхідного сигналу. На практиці не обходжений виконати умову

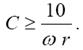
Як приклад розглядається вихідна напруга інтегруючого rC-ланцюга при дії на вхід прямокутного імпульсу (рис. 1.15, а).

Вихідна напруга на місткості в інтервалі часу від t1 до t2 змінюється згідно із законом

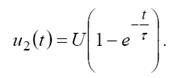
Максимальна напруга на виході

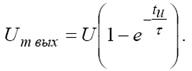
За умови, що постійна часу τ ланцюги більше тривалості вхідного імпульсу, вихідна напруга на ділянці 2 1 t t − змінюється майже по лінійному закону, тобто вихідна напруга є інтегралом вхідної напруги прямокутної форми.

Слід зазначити, що чим більше τ, тим точніше виконується операція інтеграції (закон лінійності), але вихідна напруга по величині значно менше за вхідну (рис. 1.15, в).

Час t u вих вимірюється на рівні 0,1U m вих, як це показано на рис. 1.15, б.

3.4 Порядок виконання роботи

1. Запустити на комп'ютері програму Electronics Workbench.

2. Зібрати в програмі Electronics Workbench схему відповідно до рис.1

Об’єктом дослідження є ланцюг, який утворюються із джерела напруги U, конденсатора С1, котушки індуктивності L1 та резисторів R1, R2. Перемикачі (ключі) К1, К2, К3 і К4 забезпечують комутацію схеми на той чи інший досліджуваний реактивний двополюсник і дають можливість організувати спостереження осцилограм і вимірювання струмів та напруг на різних ділянках ланцюга.

3. Підключити до досліджуваного ланцюга за допомогою ключа К1 генератор прямокутних імпульсів (зміна положення ключа здійснюється натисненням клавіші «G» на клавіатурі).

4. Для дослідження RC-ланцюга за допомогою ключа К2 (натисненням клавіші 1 на клавіатурі) під’єднується конденсатор С1. Ключ К3 встановлюється (натисненням клавіші I на клавіатурі) у положення, що забезпечує режим спостереження і вимірювання параметрів вхідного сигналу, який подається на ланцюг. Ключ К4 встановлюється у нижнє (за схемою) положення для забезпечення режимів спостереження і вимірювання параметрів струму ланцюга. Зміна положення ключа К4 здійснюється натисненням клавіші «О» на клавіатурі.

Включити схему за допомогою перемикача, або, натиснувши на клавіатурі Ctrl+G. Дочекатися появи зображення на екрані віртуального осцилографа і замалювати осцилограми вхідної напруги і струму конденсатора. Вимкнути схему, натиснувши на клавіатурі Ctrl+Т.

Визначити параметри змальованих сигналів (амплітуду, тривалість, період). За осцилограмами визначити тривалість перехідного процесу у досліджуваному ланцюзі і розрахувати постійну часу досліджуваного ланцюга. Приклад осцилограми (на екрані віртуального осцилографа) приведено на рис. 1.17.

5. Перевести ключ К4 у верхнє (за схемою) положення, що дає можливість спостерігати осцилограми напруги на конденсаторі С1 досліджуваного ланцюга.

Включити схему і, дочекавшись появи зображення на екрані віртуального осцилографа, замалювати осцилограми вхідної напруги і напруги на конденсаторі С1.

6. Для дослідження RL-ланцюга встановити ключ К2 у положення, що забезпечує це дослідження, а ключ К4 - у нижнє (за схемою) положення, яке забезпечує вимір струмів схеми.

Включити схему і, дочекавшись появи зображення на екрані віртуального осцилографа, замалювати осцилограми вхідної напруги і струму котушки.

7. Перевести ключ К4 у верхнє по схемі положення, що дає можливість спостерігати осцилограми напруги на котушці індуктивності L1 досліджуваного ланцюга.

Включити схему і, дочекавшись появи зображення на екрані віртуального осцилографа, замалювати осцилограми вхідної напруги і напруги котушки досліджуваного ланцюга. За осцилограмами визначити тривалість перехідного процесу у досліджуваному ланцюзі і розрахувати постійну часу досліджуваного ланцюга. Приклад осцилограми приведено на рис. 1.20.

3.5 Зміст звіту

До звіту заносять:

- тему та мету роботи;

- принципову схему електричного кола, яке аналізується;

- епюри струмів і напруг на окремих ділянках ланцюга досліджуваних схем;

- розрахунки тривалості перехідних процесів;

- висновки по роботі.

3.6 Контрольні питання

1. Які елементи ланцюгів називають реактивними?

2. Від яких параметрів ланцюга залежить швидкість зміни струму в ланцюги і напруги на окремих її ділянках?

3. Фізичне поняття тривалості часу перехідного процесу у ланцюзі з реактивними елементами.

4. Фізичне поняття «постійної часу ланцюга» з реактивними елементами.

5. Визначення постійної часу rL - ланцюга і вплив величини опору на тривалість перехідного процесу.

6. Визначення постійної часу ланцюга графічно і аналітично.

7. Диференціюючи ланцюги і фізичний сенс процесів, що відбуваються в них.

8. Інтегруючи ланцюги і фізичний сенс процесів, що відбуваються в них.

9. 5. Визначення постійної часу rС - ланцюга і вплив величини опору на тривалість перехідного процесу.

10. Визначити умову, при якій rC-ланцюг є диференціюючим.

11. Визначити умову, при якій rC-ланцюг є інтегруючим. Вибір r і С інтегруючого ланцюга.

12. сформулюйте закони комутації.

Лабораторна робота № 2

дослідження перехідних процесів в лінійних ланцюгах другого порядку

1.1 Мета роботи:

експериментальне дослідження перехідного процесу в ланцюзі з послідовним з'єднанням RLC- елементів при включенні її в ланцюг постійного струму.

1.2 Зміст роботи:

для заданого електричного кола (рис.2.1):

- встановити задані (за варіантами) параметри елементів;

- скласти характеристичне рівняння та знайти його коріння;

- по результатам рішення визначити вид перехідного процесу в досліджуваному ланцюзі;

- провести необхідні вимірювання величин струмів та напруги (табл. 2.2);

- зарисувати епюри струмів та напруги на елементах досліджуваного ланцюга;

1.3 Теоретичні відомості:

аналізу перехідного процесу електричного кола другого порядку.

При всіх змінах в електричному ланцюзі: включенні, виключенні, короткому замиканні, коливаннях величини якого-небудь параметра і т.п. - в ній виникають перехідні процеси, які не можуть протікати миттєво, оскільки неможлива миттєва зміна енергії, яка запасена в електромагнітному полі ланцюга. Таким чином, перехідний процес обумовлений невідповідністю величини запасеної енергії в магнітному полі котушки і електричному полі конденсатора її значенню для нового стану ланцюга.

При перехідних процесах можуть виникати великі перенапруження, надструми, електромагнітні коливання, які можуть порушити роботу пристрою аж до виходу його з ладу. У інших випадках, перехідні процеси знаходять корисне практичне застосування (у різних електронних генераторах). Все це обумовлює необхідність вивчення методів аналізу нестаціонарних режимів роботи ланцюга.

Основні методи аналізу перехідних процесів в лінійних ланцюгах:

1. Класичний метод, що полягає в безпосередній інтеграції диференціальних рівнянь, які характеризують електромагнітний стан ланцюга.

2. Операторний метод, що полягає в рішенні системи рівнянь, алгебри, щодо зображень шуканих змінних з подальшим переходом від знайдених зображень до оригіналів.

3. Частотний метод, що заснований на перетворенні Фур'є і знаходить широке застосування при рішенні задач синтезу.

4. Метод розрахунку за допомогою інтеграла Дюамеля, використовуваний при складній формі кривої збуджуючої дії.

5. Метод змінних стану, що є впорядкованим способом визначення електромагнітного стану ланцюга на основі рішення системи диференційних рівнянь першого порядку, записаних в нормальній формі (формі Коші).

Оскільки короткий виклад всіх вище перелічених методів скрутно, нижче приведено короткий опис тільки класичного методу аналізу.

Класичний метод розрахунку

Класичний метод розрахунку перехідних процесів полягає в безпосередній інтеграції диференціальних рівнянь, які характеризують зміни струмів і напружень на ділянках ланцюга в перехідному процесі.

У загальному випадку при використанні класичного методу розрахунку складаються рівняння електромагнітного стану ланцюга по законах Ома і Кірхгофа для миттєвих значень напружень і струмів, зв'язаних між собою на окремих елементах ланцюга співвідношеннями:

для резистора (ідеальний активний опір)

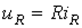(2.1)

для котушки індуктивності (ідеальна індуктивність)

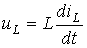(2.2)

для конденсатора (ідеальна місткість)

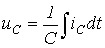(2.3)

Для послідовного ланцюга, що містить лінійні резистор R, котушку індуктивності L і конденсатор С, при її підключенні до джерела з постійною напругою u (рис. 1.1) можна записати

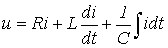(2.4)

Диференціюючи цей вираз одержимо лінійне диференціальне рівняння другого порядку

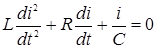. (2.5)

Порядок даного рівняння рівний числу незалежних накопичувачів енергії в ланцюзі. Під ними розуміються котушки індуктивності і конденсатори в спрощеній схемі, яка одержується з початкової шляхом об'єднання індуктивностей і відповідно ємностей елементів, з'єднання між якими є послідовними або паралельними.

У загальному випадку порядок диференціального рівняння визначається співвідношенням

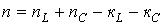(2.6)

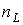де и 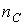- відповідно число котушок індуктивності і конденсаторів після вказаного спрощення початкової схеми; 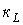- число вузлів, в яких сходяться тільки гілки, що містять котушки індуктивності (відповідно до першого закону Кірхгофа струм через будь-яку котушку індуктивності в цьому випадку визначається струмами через решту котушок); 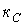- число контурів схеми, гілки яких містять тільки конденсатори (відповідно до другого закону Кірхгофа напруга на будь-якому з конденсаторів в цьому випадку визначається напругою на інших).

Наявність індуктивних зв'язків на порядок диференціального рівняння не впливає.

У рішенні рівняння (2.5) класичним методом примушена складова струму відсутня а форма запису вільної складової струму залежить від виду коріння характеристичного рівняння яке виходить шляхом заміни 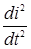на р² , 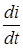- на р і р⁰= 1.

LP²+RP+1/C=0 (2.7)

коріння цього характеристичного рівняння визначається як

Р_1,2 = 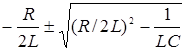(2.8)

Позначивши

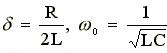
Одержимо

Р_1,2 = 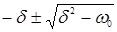(2.9)

Залежно від співвідношення  и ₀ можливі три випадки:а)  >  ₀ , т.е.

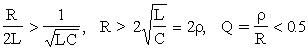(аперіодичний процес).У площині комплексного змінного коріння характеристичного рівняння лежить на речовинній осі Напруга на елементах U_R=Ri=

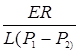(е^p1t-е^p2t),U_L=L

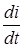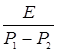(P₁е^p1t-P₂е^p2t), U_C=E-U_R-U_L=E[1+ (P2еp1--P1еp2t)].

Графіки залежностей U_R, U_L, U_C від часу приведені (рис.2.3).

б)   _ , R = 2 , Q = 0.5 (критичний режим),Р_1,2 =- , i(t)=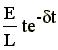

.Форма кривих залежностей струму і напруги на R, L, C від часу аналогічна аперіодичному режиму, умова Q=0.5 є граничною умовою існування в ланцюзі аперіодичних процесів;в)

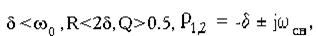(коливальний процес).

Коріння характеристичного рівняння комплексно-зв'язане (рис.2.4).

Струм в ланцюзі є затухаючим гармонійним коливанням, амплітуда якого зменшується в часі по експоненціальному закону (рис.2.5).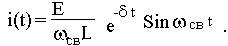

Напруга на елементах ланцюга

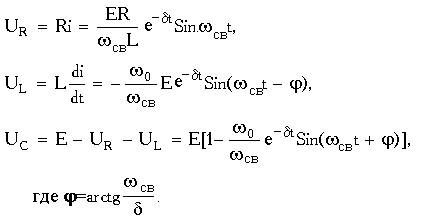Швидкість зменшення амплітуди коливань оцінюють величиною декременту загасання Δ = e^δTсвде Т_св - період вільних коливань,і логарифмічним декрементом загасанняθ = ln Δ = δ Tсв = Tсв / τ_св.при визначенні декремента загасання по експериментально одержаній осцилограмі струму його зручно знаходити як відношення амплітуд першого і другого періодів затухаючих коливаньΔ = Im₁ / Im_2,як показано на рис 2.7,

1.4 Порядок виконання роботи:

1. Зібрати (на екрані монітору ПК) у програмі Electronics Workbench за допомогою стандартизованих елементів (табл. 2.1), схему заданого електричного кола (рис 2.8).

2. Включити зібрану схему за допомогою перемикача, або натиснувши на клавіатурі ПК кнопки Ctrl+G.

3. Натиснути клавішу «Пробел». на екрані віртуального осцилографа повинні з'явитися імпульс вхідної дії і сигнал реакції схеми на цю дію.

4. Вимкнути схему за допомогою того ж перемикача, або натиснувши на клавіатурі ПК Ctrl+Т.

5. за допомогою шкал віртуального осцилографа визначити амплітудні і часові характеристики перехідного процесу того, що протікає в схемі. Зарисувати одержані епюри напружень. Одержані дані занести в таблицю 1.2

Таблиця 2.1 – Початкові значення за варіантами

№. варіанта	L, мГ	С, мкФ	R, Ом
1	10	0,47	22
2	10	1	22
3	40	0,1	100
4	40	0,22	100
5	40	0,47	100
6	40	1	100
7	100	0,1	220
8	100	0,22	220
9	140	0,1	150
10	200	0,1	220

Таблиця 2.2 – Числові дані характеристик електричного кола

	Розрахункові дані						Експериментальні дані
Величина	Р₁	Р₂	f₀	δ	Tсв	Q	Im₁	Im₂	Tсв	δ	Q
Дані замірів:

6. Показати на комплексній площині розташування коріння характеристичного рівняння. Зробити висновок про характер перехідного процесу.

7. розрахувати коефіцієнт загасання δ, частоту вільних коливань, а також постійну інтегрування А = Е / (ω_СВL)

1.5 Зміст звіту

До звіту заносять:

- тему і мету роботи;

- принципову схему електричного кола, яке аналізується;

- теоретичний розрахунок параметрів електричного кола, яке аналізується

- результати вимірювання струмів та напруг на окремих ділянках досліджуваного кола;

- результати розрахунку параметрів перехідного процесу;

- епюри вхідної дії і перехідного процесу;

- висновки по роботі.

1.6 Контрольні питання

1. як складається характеристичне рівняння?

2. які види перехідних процесів можливі в RLC - ланцюгах залежно від виду коріння характеристичного рівняння.

3. як визначаються начальне умови для досліджуваної схемі?

4. Що характеризує декремент затухання і як він визначається?

5. як по значенню комплексного кореня визначити постійну часу обгинання?

6. як по значенню комплексного кореня визначити період вільних коливань?

Лабораторна робота №3

ДОСЛІДЖЕННЯ нелінійних ланцюгів ПОСТІЙНОГО СТРУМУ

2.1 Мета роботи: Експериментальне дослідження розподілу струмів і напружень в нелінійному електричному ланцюзі (ЕЛ) постійного струму. Визначення струмів і напружень в нелінійному ЕЛ графоаналітичними методами.

2.2 Зміст роботи:

Для заданого електричного кола (рис.3.1):

- встановити задані параметри джерела живлення електричного кола;

- провести необхідні вимірювання величин струмів та напруги;

- розрахувати параметри кола постійного струму з нелінійними елементами;

- оцінити похибки вимірювань та зробити висновки щодо режимів роботи лінії. При оцінці похибок вимірювань вважати межею вимірювань Iмах = 1А (для амперметрів), Vмах = 10 В (для вольтметрів), а за клас точності прийняти для всіх приладів δ = 0,1.

2.3 Теоретичні відомості:

ЕЛ звуться нелінійними, якщо в ланцюзі є хоч би один нелінійний елемент (НЕ). У таких елементів вольт-амперна характеристика (ВАХ) (I = f (U)) є нелінійною функцією, оскільки опір цього елементу залежить від величини і напряму струму, що протікає через нього, або від величини і знаку напруги, прикладеної до нього. Нелінійні елементи описуються нелінійними характеристиками, які не мають строгого аналітичного виразу, визначаються експериментально і задаються табличний або графіками.

Нелінійні елементи можна розділити на двох - і багатополюсні. Останні містять три (різні напівпровідникові і електронні тріоди) і більш (магнітні підсилювачі, багатообмоточні трансформатори, тетроди, пентоди і ін.) полюсів, за допомогою яких вони під'єднуються до електричного ланцюга. Характерною особливістю багатополюсних елементів є те, що в загальному випадку їх властивості визначаються сімейством характеристик, що представляють залежності вихідних характеристик від вхідних змінних і навпаки: вхідні характеристики будують для ряду фіксованих значень одного з вихідних параметрів, вихідні - для ряду фіксованих значень одного з вхідних.

За іншою ознакою класифікації нелінійні елементи можна розділити на інерційні і неінерційні. Інерційними називаються елементи, характеристики яких залежать від швидкості зміни змінних. Для таких елементів статичні характеристики, що визначають залежність між діючими значеннями змінних, відрізняються від динамічних характеристик, що встановлюють взаємозв'язок між миттєвими значеннями змінних. Неінерційними називаються елементи, характеристики яких не залежать від швидкості зміни змінних. Для таких елементів статичні і динамічні характеристики співпадають.

Залежно від виду характеристик розрізняють нелінійні елементи з симетричними і несиметричними характеристиками. Симетричною називається характеристика, не залежна від напряму визначальних її величин, тобто що має симетрію відносно почала системи координат: 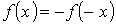. Для несиметричної характеристики ця умова не виконується, тобто 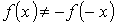. Наявність у нелінійного елементу симетричної характеристики дозволяє у цілому ряді випадків спростити аналіз схеми, здійснюючи його в межах одного квадранта.

У сучасних засобах автоматики, радіотехніки і обчислювальної техніки широке застосування знаходять НЕ (діоди, транзистори, тиристори і т.д.), які мають різні по формі ВАХ.

Дата добавления: 2019-07-15; просмотров: 154; Мы поможем в написании вашей работы!

Поделиться с друзьями:

⇐ Предыдущая 123 4 5 Следующая ⇒

Мы поможем в написании ваших работ!