Графическое оформление расчетов и анализ движения выходного звена
ВВЕДЕНИЕ
В данной курсовой работе исследуется движение механизма рабочей машины.
Целью работы является подготовка данных для прочностного расчета. Данные для прочностного расчета мы получаем при проведении силового анализа. Для того чтобы провести силовой анализ нам необходимо иметь данные, получаемые при анализе динамики установившегося движения, а также при структурном анализе.
Исходными данными для анализа являются значения, получаемые при кинематическом анализе механизма. При проведении анализа нам необходимо иметь данные по структурному анализу.
Целью кинематического анализа механизма является построение функций, исчерпывающе описывающих преобразованием движения в механизме.
Найденные при кинематическом анализе функции используются для построения динамической модели машины и определения истинного закона ее движения.
Для расчетов неизвестных данных в ходе работы была использована
программа Microsoft Office Excel. Так же для наглядного представления графики и диаграммы выполнялись при помощи программы Компас -3D V16.
АНАЛИЗ РЫЧАЖНОГО МЕХАНИЗМА
Исследование рычажного механизма выполним в следующей последовательности:
· Структурный анализ;
· Кинематический анализ;
· Анализ динамики установившегося движения;
· Силовой анализ.
Задачи каждого пункта исследования, а также допущения при решении этих задач сформируем в соответствующих подразделах.
|
|
|
Исходные данные составляют:
· Схема механизма (рис. 1.);
· Кинематические и динамические параметры (табл. 1.).
Схема механизма:
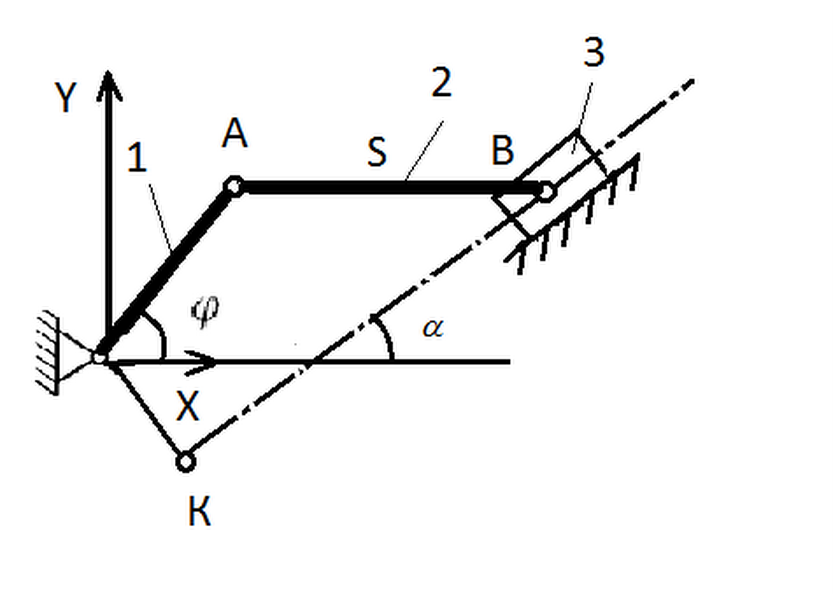
Рис. 1. Рычажный механизм
Таблица 1.
Кинематические и динамические параметры
| Вар. | r (OA), м | l (AB), м | d (AS), м | e (OK), м | a, град | wср, с-1 | I10, кгм2 | m2, кг | IS2, кгм2 | m3, кг | P1, Н | P2, Н | P3, Н | H1, м | H2, м | H3, м | d |
| A-36 | 0,06 | 0,24 | 0,06 | 0 | 180 | 220 | 0,006 | 0,36 | 0,003 | 0,36 | 0 | 0 | 1000 | 0 | 0 | 0,4 | 0,03 |

Рис. 2. График сил полезного сопротивления
Структурный анализ
Задачи структурного анализа:
1. Анализ строения механизма на уровне звеньев и кинематических пар, подсчет степени подвижности;
2. Анализ строения механизма на уровне структурных групп.
Для упрощения решения этих и последующих задач примем следующие допущения:
1. Звенья абсолютно жесткие;
2. Отсутствуют зазоры в кинематических парах.
Определение степени подвижности механизма
В данной курсовой работе следующие обозначения звеньев механизма:
|
|
|
0–стойка, 1–кривошип, 2–шатун, 3–ползун.
Учитывая допущение 1, степень подвижности механизма определим по формуле Чебышева:

| (1) |
Таблица 2.
Кинематические пары
| № кинематической пары | Обозначение пары | Название пары | Класс пары | Звенья, входящие в пару |
| 1 | О | вращательное | 5 | 0,1 |
| 2 | А | вращательное | 5 | 1,2 |
| 3 | В | вращательное | 5 | 2,3 |
| 4 | В0 | поступательная | 5 | 3,0 |
n – число подвижных звеньев , n = 3 p5 – число пар пятого класса, p5 = 4.
 .
.
Вывод: Степень подвижности равна единице, что свидетельствует о наличии только одного входного звена, звено 1(ОА). Если этому звену задать движение с некоторой угловой скоростью, то все остальные звенья механизма будут совершать строго определенные движения.
1.2. Определение класса механизма
Класс механизма определим по методу Ассура – Артоболевского.

Рис.3. Исходный механизм I(0,1) Рис.4. Группа Ассура II класса 2.вида II(2,3) 1порядка
Формула механизма:  . (2)
. (2)
Исследуемый механизм состоит из механизма первого класса и группы Ассура (кинематическая цепь с нулевой степенью подвижности) второго класса, второго порядка.
|
|
|
Вывод: на основании формулы (2) заключаем, что исследуемый механизм (рис.1.) второго класса, так как в его составе нет группы выше второго класса.
2. Кинематический анализ механизма
Кинематический анализ - это исследуемый механизм без учета сил.
Задачи кинематического анализа:
1. Анализ положения звеньев и траекторий шарнирных точек и центров масс звеньев графическим методом;
2. Аналитическое определение кинематических функций: функций положений, аналогов скоростей и аналогов ускорений центров масс звеньев и кинематических пар; функций углового положения, аналогов угловых скоростей и угловых ускорений звеньев;
3. Численное исследование аналогов скоростей и ускорений;
4. Определение крайних положений механизма и величины хода выходного звена.
Исходными данными для анализа является схема механизма и размеры звеньев.
При решении поставленных задач примем следующие допущения:
1. Звенья абсолютно жесткие;
2. Отсутствуют зазоры в кинематических парах.
2.1. Анализ характера движения звеньев
Любое движение можно представить как комбинацию двух видов движения: поступательного и вращательного. В данном пункте установим характер движения каждого звена и необходимый набор параметров.
|
|
|
На рис. 1 изображена схема механизма с номерами звеньев.
Механизм имеет три подвижных звена.
Звено 1 – кривошип - совершает вращательное движение вокруг неподвижной оси, проходящей через точку 0. Точка А движется по окружности. Входное звено, параметры его движения задаются.
Звено 2 – шатун совершает сложно-плоское движение, т.е. вращается и перемещается поступательно. Параметры движения данного звена:  – угол поворота звена относительно оси х, положение точки А, определяемое положением кривошипа. Точка В движется поступательно.
– угол поворота звена относительно оси х, положение точки А, определяемое положением кривошипа. Точка В движется поступательно.
Звено 3 – ползун совершает возвратно-поступательное движение по прямолинейной направляющей, расположенной под углом  к оси х, и, смещённой от точки 0 вниз на величину е (ОК). Положение звена описывается перемещением точки В (SВ).
к оси х, и, смещённой от точки 0 вниз на величину е (ОК). Положение звена описывается перемещением точки В (SВ).
2.2. Построение плана положений механизма
Метод решения данной задачи – графический. План положений механизма строим на первом листе с масштабным коэффициентом равным:
 .
.
Построение плана механизма выполним в следующей последовательности:
· Строим траекторию движения точки А; находим начальное положение;
· Разбиваем траекторию на 12 равных частей от начального положения кривошипа;
· Проводим направляющую под углом a на расстоянии е от точки 0;
· Методом засечек на направляющей находим положения точки В.
· Методом засечек на шатуне расстояние d находим положение токи S.
Начальное положение кривошипа определяется углом φ рис.5:
Сначала мы выбираем систему координат, затем проводим направляющую под заданным углом. Потом находим начальное положение, для этого: из начала координат проводим круг с радиусом r, затем радиусом равным r+L в выбранном масштабе проводим круг, до пересечения с направляющей и из этой точки проводим прямую в центр координат. Это и есть начальное положение механизма.

Рис.5.
 ;
;
 .
.
2.3. Вывод зависимостей и расчет кинематических параметров.
Звено, ОА вращающееся вокруг неподвижной оси, т.е. образующее со стойкой 0 вращательную кинематическую пару (рис. 5), его положение определяется одним параметром – угловой координатой φ.

Рис. 5. Входное звено.
Проецируем кривошип (ОА) на координатные оси:

| (4) (5) |
Далее выведем зависимости аналогов uj и аj. Задачу решаем аналитически с использованием метода векторных контуров. Для получения зависимостей составляем векторные контуры. Углы отсчитываем от оси х против часовой стрелки, а для входного звена в направлении вращения.

Рис.6. Векторный контур OABKО.
Составим уравнение замкнутости контура ОАВКО в векторном виде:
 . .
| (6) |
Перепишем это векторное уравнение, оставив в левой части векторы, направление которых зависит от подвижных звеньев.

Спроектируем полученное векторное уравнение на координатные оси:
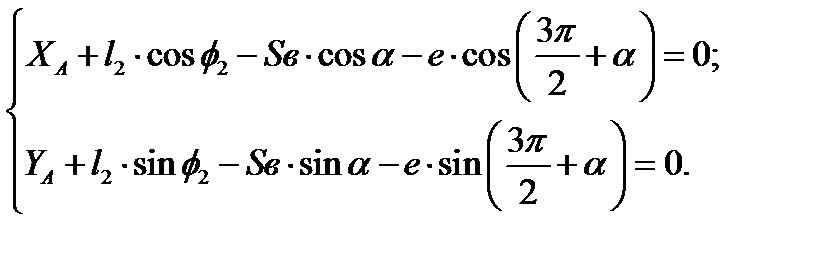
| (7) |
Используем формулы приведения:

| (8) |
Первое уравнение системы умножаем на  , второе на
, второе на 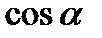 , а затем вычитаем из второго первое и получим:
, а затем вычитаем из второго первое и получим:

| (9) |
Подставляя во вторую строчку уравнение (9) значения известных величин получаем значение угла  :
:
 град.
град.
Для нахождения скорости точки. В и аналога угловой скорости, продифференцируем уравнение (8) по  , получим:
, получим:

| (10) |
Первое уравнение системы умножаем на 
 , второе на
, второе на 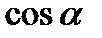 , а затем вычитаем из второго первое, подставим значения известных величин во вторую строчку уравнения (10), получим:
, а затем вычитаем из второго первое, подставим значения известных величин во вторую строчку уравнения (10), получим:

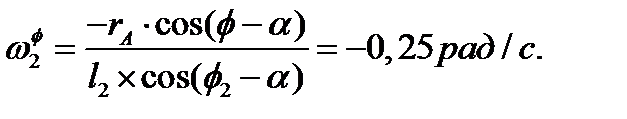
Подставляем значение найденной величины в первую строчку уравнение системы (10), получаем:
 =-0,0295 м.
=-0,0295 м.
Для определения аналога ускорения точки. В и аналога углового ускорения продифференцируем уравнение (10) по  , получим:
, получим:

| (11) |
Первое уравнение системы умножаем на 
 , второе на
, второе на 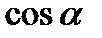 , а затем вычитаем из второго первое, подставим значения известных величин в одно из уравнений, получим:
, а затем вычитаем из второго первое, подставим значения известных величин в одно из уравнений, получим:


Подставляем значение найденной величины в первую строчку уравнения системы (11), получаем:
 .
.
Таблица 3.
Графическое оформление расчетов и анализ движения выходного звена
По результатам расчетов строим графики и годографы кинематических параметров. Построения выполняем на первом листе чертежей.
Графики строим в зависимости от угла поворота кривошипа с масштабным коэффициентом:
 .
.
График перемещения выходного звена строим по результатам измерений, по результатам расчетов снятых с плана положений механизма масштабным коэффициентом: 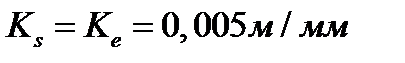 .
.
Ниже приведены масштабные коэффициенты графиков аналогов скоростей и ускорений:


Параметры движения центра масс шатуна представляем в виде годографов:

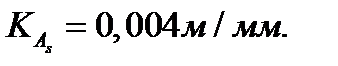
Годографы показаны на листе 1.
Диаграмма аналогов угловой скорости и углового ускорения строятся с коэффициентами: 
 .
.
По графикам листа 1 определяем максимальное значение кинематических параметров: 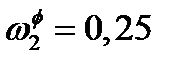 м;
м;  ;
; 


Холостой ход начинается в 5`положении механизма и заканчивается в 1-ом положении, т.е. холостой ход механизма лежит в интервале от  =5,3904рад до
=5,3904рад до  =8,5817 рад.
=8,5817 рад.
Рабочий ход начинается с 0-ого положения механизма и заканчивается в 5` положении, т.е. рабочий ход механизма лежит в интервале от  =2,2985 рад до
=2,2985 рад до  =5,3904рад.
=5,3904рад.
По графикам аналогов скоростей и ускорений определяем участки ускоренного и замедленного движения:
· от  до
до  = 3,3457 рад – ускоренное движение;
= 3,3457 рад – ускоренное движение;
· от  до
до  =5,3904 рад - замедленное движение;
=5,3904 рад - замедленное движение;
· от 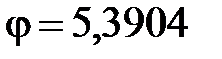 до
до  рад – ускоренное движение;
рад – ускоренное движение;
· от  до
до  рад – замедленное движение.
рад – замедленное движение.
3. Анализ динамики установившегося движения
Задачами данного подраздела ставим:
1. Построение динамической модели механизма;
2. Численный анализ параметров динамической модели, угловой скорости и углового ускорения главного вала (без маховика);
3. Определение работы сопротивления момента и мощности двигателя;
4. Оценка неравномерности хода машины;
5. Определение момента инерции маховика;
6. Определение угловой скорости и углового ускорения главного вала механизма с маховиком.
Для упрощения решения поставленных задач примем следующие допущения:
1. Пренебрегаем трением в кинематических парах и вредным сопротивлением среды;
2. Момент, развиваемый двигателем, считаем постоянным на всем периоде установившегося движения;
3. Полезное сопротивление зависит лишь от положения механизма.
3.1.Формирование динамической модели машины
Для определения истинных параметров создания динамической модели машины, которая для механизма с одной степенью подвижности представляет собой условный двухзвенный механизм с одним неподвижным, другим подвижным звеньями. Подвижное звено нагружено силами эквивалентными по действию силам приложенным к звеньям. Силы для учета сил инерции находятся через приведенный момент инерции всех звеньев машины.
С их помощью определяются параметры движения подвижного звена модели из энергетического и дифференциального уравнений движения.
Рассмотрим решение задачи динамики машин - определение закона движения машины по заданным действующим на нее силах. На основе анализа периодических колебаний скорости главного вала оценивается неравномерность хода машин. Если коэффициент неравномерности хода превышает допустимую величину δ, то для уменьшения колебания скорости на главный вал устанавливается маховик. Расчетные формулы:
Приведенная инертность определяется на основании равенства кинетических энергий.
Кинетическая энергия приведенной меры инертности, равна сумме кинетической энергии приводимых мер инертности.
Приведенный момент инерции:
 .
.
Момент сил сопротивления:
 ;
;
 .
.
По полученным данным на втором листе чертежа строим графики: Pпс, график приведенного момента сил Ms (на этом же графике строим Md), графики работ Ас и Аd, графики угловой скорости и ускорения, график приведенного момента инерции  и
и  , диаграмму Виттенбауэра.
, диаграмму Виттенбауэра.
Строим график суммарной работы AΣ, координаты которого равны разности Ac и Ad.
Таблица 4.
Приведенные параметры механизма
3.2. Оценка неравномерности движения
Запишем формулы для ω(t) и ε(t):
 ; ;
| (17) |
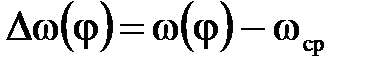 . .
| (18) |
Оставшиеся значения  приведены в таблице 1.6
приведены в таблице 1.6
 . .
| (20) |
Колебания скорости главного вала машины в режиме установившегося движения – периодические. Их амплитуду принято оценивать безразмерным коэффициентом d.
Его определяют по формуле:
 . .
| (21) |
 рад/с;
рад/с;  рад/с;
рад/с; 
Так как, 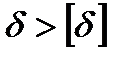 , то необходимо на входное звено установить маховик, который (его момент инерции) увеличит постоянную составляющую приведенного момента инерции.
, то необходимо на входное звено установить маховик, который (его момент инерции) увеличит постоянную составляющую приведенного момента инерции.
Оставшиеся значения  приведены в таблице:
приведены в таблице:
Таблица 5.
| ω | Δω | ε | ΔIпр |
| 220 | 0 | 1373,46216 | 0,000917 |
| 212,7113047 | -7,288695298 | -5783,14296 | 0,001531 |
| 195,1569332 | -24,8430668 | -6787,53301 | 0,002503 |
| 183,0937769 | -36,90622313 | -2361,02866 | 0,002592 |
| 184,0319184 | -35,96808159 | 2625,856741 | 0,001881 |
| 193,0659166 | -26,93408336 | 3547,43696 | 0,001177 |
| 199,7972838 | -20,20271616 | 1327,507703 | 0,000917 |
| 199,5225893 | -20,47741074 | -1435,44789 | 0,001177 |
| 193,5959324 | -26,40406756 | -2578,18585 | 0,001881 |
| 188,4461334 | -31,55386655 | -641,688267 | 0,002592 |
| 192,4478467 | -27,55215328 | 3801,390369 | 0,002503 |
| 207,6857396 | -12,31426043 | 7015,369864 | 0,001531 |
| 220 | 0 | 1373,46216 | 0,000917 |
3.3. Расчет маховика
Задача: Определить момент инерции маховика, обеспечивающий заданный коэффициент неравномерности хода машины.
 =223,3 рад/с; =223,3 рад/с;
| (22) |
 = 216,7рад/с. = 216,7рад/с.
| (23) |
Момент инерции маховика определяем методом Виттенбауэра. Строим диаграмму Виттенбауэра по известным значениям. АΣ и ∆Iпр.
Вычисляем значения углов ψmax и ψmin по формулам:
 ; ;
| (24) |
 . .
| (25) |


ААΣ= -26,55 Дж;
АВΣ=1,4767 Дж;
IАпр=0,0024675 кг*м^2;
IВпр= 0,0009396 кг*м^2.
К построенной диаграмме проводим касательные под углами tg  и определим точки касания А и В, после чего замеряем K1.
и определим точки касания А и В, после чего замеряем K1.
Рис. 7.Диаграмма Виттенбауэра.
Расчет момента инерции маховика производим по формуле:
 кг*м^2. кг*м^2.
| (26) |
3.4. Определение истинных скоростей и ускорений
Зная положение точек  ,
, 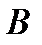 и
и 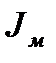 , можно рассчитать скорости и ускорения главного вала в любой точке цикла.
, можно рассчитать скорости и ускорения главного вала в любой точке цикла.
Угловую скорость рассчитываем по формуле:
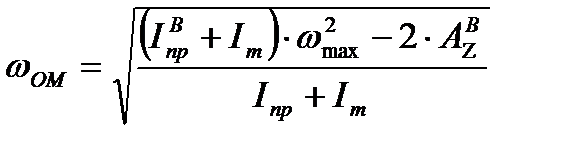 ; ;
| (27) |

 ; ;
| (28) |


Остальные значения приведены в табл. 6.
Находим ускорения центров масс звеньев и угловые ускорения звенья по формулам:
 ; (40)
; (40)
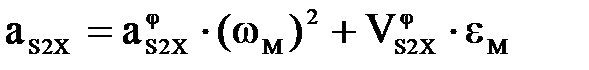 ; (41)
; (41)
 ; (42)
; (42)
 . (43)
. (43)
На чертеже строим графики 
 со следующими коэффициентами:
со следующими коэффициентами:  ;
;  ;
;  .
.
Таблица 6.
Параметры движения с учетом маховика
| ωm(ϕ) | ωm | εm(ϕ) |
| 223,2082706 | 3,208270647 | 215,9685 |
| 221,9680379 | 1,968037934 | -1067,16 |
| 218,7417554 | -1,25824460 | -1398,97 |
| 216,7266527 | -3,27334729 | -321,087 |
| 217,3556022 | -2,64439778 | 695,2464 |
| 219,1092754 | -0,89072456 | 694,3009 |
| 220,2006804 | 0,200680369 | 208,7425 |
| 220,0455579 | 0,045557852 | -328,198 |
| 218,8074279 | -1,19257214 | -634,593 |
| 217,5882249 | -2,41177512 | -229,139 |
| 218,2934365 | -1,70656350 | 853,3697 |
| 221,1630017 | 1,163001674 | 1314,799 |
| 223,2082706 | 3,208270647 | 215,9685 |
4.Силовой расчет механизма
В данном пункте будут определены силы взаимодействия звеньев механизма. Используем уравнение равновесия составленных для отдельного звена или структурной группы механизма.
Цель: определение сил и моментов в кинематических парах, необходимых для прочностного расчет.
Задачи:
1. Определение реакций в кинематических парах;
2. Определение уравновешивающей силы.

Рис.8.
Для того чтобы реакции сделать внешними силами используется принцип освобождаемости от связи: цепи рассоединяются в кинематических парах и рассматриваются в состоянии равновесия, действия отсоединенной цепи заменяются реакцией.
Отсоединяемые системы должны быть статически определимыми. В механизме такими системами являются группы Ассура. Исследования начинают с последней присоединенной в процессе синтеза группы Ассура к исходному механизму.
4.1. Расчет сил
Сила полезного сопротивления
 ;
;
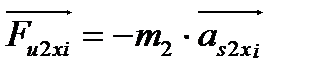 ;
;
 ;
;
 ;
;
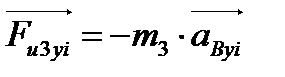 ;
;
 .
.
Расчёт сил инерций приложенных к точкам. При нахождении реакций связей обусловились, что при решении данной задачи мы будем пользоваться принципом Даламбера и для этого нам нужно найти силы инерции которые приложены к точкам.
 ,
,  ,
,  Н;
Н;
и  ,
,  ,
,  Н.
Н.
Момент инерции:
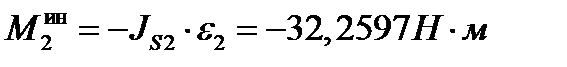 ;
;
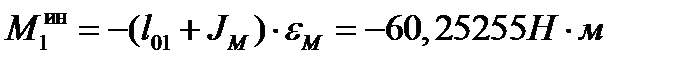 .
.
Вычерчиваем группу Ассура со звеньями 2 и 3 в конкретном положении и показываем все силы, которые действуют на них. Рис.9.
Рис.9. Группа Ассура.
4.2. Расчет групп Ассура
Составляем уравнение равновесия, Группы Ассура под действием сил:
1) 



2) 



3) 

Из 2) 
Из 3) 



Для нахождения реакции  :
:
 ;
;

4.3.Расчет исходного механизма
Составляем уравнение равновесия, исходного механизма под действием сил:

Находим  Н*м.
Н*м.
Сравним полученный результат с результатом, найденным в динамическом анализе:


Рис.10. Исходный механизм
ЗАКЛЮЧЕНИЕ
В данной курсовой работе по теории машин и механизмов был выполнен анализ рычажного механизма; в структурном анализе были рассмотрены и найдены особенности строения механизма – степень подвижности, входное звено, группы Ассура которые входят в механизм, класс механизма.
В кинематическом анализе исследовалось движение механизма в геометрическом аспекте. Было проанализировано движение выходного звена (ползун). Так же были построены функции, описывающие преобразование движения в механизме. Углы входного звена при крайних положениях механизма  ,
,  . Определены кинематические параметры
. Определены кинематические параметры  ;
;  град,
град,  ,
,  ,
,  м,
м,  ,
, 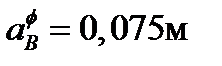
В анализе динамики установившегося движения для построения динамической модели машины определены параметры динамической модели  ,
,  . Оценив неравномерность хода машины, добавляем в машину маховик с моментом инерции
. Оценив неравномерность хода машины, добавляем в машину маховик с моментом инерции  для того чтобы снизить инерционную нагрузку и таким образом повысить долговечность машины. Определены параметры движения механизма с маховиком
для того чтобы снизить инерционную нагрузку и таким образом повысить долговечность машины. Определены параметры движения механизма с маховиком  .
.  ,
,  .
.
В силовом анализе были исследованы силы, действующие на механизм, и вызванные под их действием моменты инерции и реакции, возникающие в звеньях при их движении, так же после анализа входного звена был момент равный Мd=9,729797Нм.
Определены значения реакций  ,
,  .
.
В ходе выполнения курсовой работы были выполнены поставленные задачи и достигнуты цели, на основании которых можно сделать следующие выводы:
Движение можно задавать только одному звену.
Входное звено – кривошип ОА.
Степень подвижности равна единице, что свидетельствует о наличии только одного входного звена, звено 1 (ОА). Если этому звену задать движение с некоторой угловой скоростью, то все остальные звенья механизма будут совершать строго определенные движения
Данный механизм является механизмом второго класса.
Исследуемый механизм второго класса, так как в его составе нет группы выше второго класса.
Вращение входного звена происходит с переменной скоростью.
Доказана необходимость установки маховика.
Так как 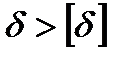 ,то необходимо на входное звено установить маховик, который (момент инерции которого) увеличит постоянную составляющую приведенного момента инерции.
,то необходимо на входное звено установить маховик, который (момент инерции которого) увеличит постоянную составляющую приведенного момента инерции.
СПИСОК ЛИТЕРАТУРЫ:
1. Артоболевский И. И. Теория механизмов и машин, М.: Наука, 1975
2. Черная Л.А., Черный Б.А. Исследование рычажных механизмов с применением ЭВМ. Методические указания к курсовому проекту проектирования по теории механизмов и машин, Хабаровск, изд. ХПИ, 1979.
Дата добавления: 2019-07-15; просмотров: 229; Мы поможем в написании вашей работы! |

Мы поможем в написании ваших работ!
