Задача 4. Решить задачу по подобию задачи 3.
Механика сплошной среды
1. ЛАГРАНЖЕВО И ЭЙЛЕРОВО ОПИСАНЕ ДВИЖЕНИЯ
При изучении движения сплошной среды можно использовать два подхода: один из них называют лагранжевым, другой – эйлеровым.
При лагранжевом подходе интересуются тем, что происходит с индивидуальными точками (частицами) сплошной среды. При движении среды ее характеристики для разных индивидуальных частиц меняются со временем по-разному. Чтобы отличить одну индивидуальную частицу от другой, надо на них “поставить метки”. Это можно сделать, например, если присвоить каждой частице свой набор из трех чисел, который играет роль “имени”. Эти числа называют лагранжевыми координатами и часто обозначают буквами x1, x2, x3. Лагранжевы координаты индивидуальной точки не меняются в процессе движения.
При лагранжевом описании все величины рассматриваются как функции лагранжевых координат (x1, x2, x3) и времени t. В качестве x1, x2, x3 часто используют 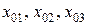 – значения координат точек пространства, в которых рассматриваемые индивидуальные частицы находились в начальный момент времени.
– значения координат точек пространства, в которых рассматриваемые индивидуальные частицы находились в начальный момент времени.
Законом движения называются функции, описывающие зависимость пространственных координат 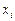 индивидуальных точек от времени t. Закон движения записывается в виде:
индивидуальных точек от времени t. Закон движения записывается в виде:
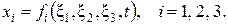
Компоненты скорости 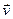 и ускорения
и ускорения 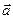 частиц сплошной среды в декартовой системе координат при лагранжевом описании вычисляются по формулам:
частиц сплошной среды в декартовой системе координат при лагранжевом описании вычисляются по формулам:
|
|
|
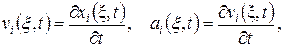
где для краткости использовано обозначение x = (x1, x2, x3).
При эйлеровом подходе интересуются тем, что происходит в точках пространства, через которые движется среда. Величины, характеризующие движение сплошной среды, рассматриваются при эйлеровом подходе как функции пространственных координат 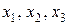 и времени t. Например, величина
и времени t. Например, величина 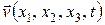 – это скорость частицы сплошной среды, которая в момент времени t находится в точке пространства с координатами
– это скорость частицы сплошной среды, которая в момент времени t находится в точке пространства с координатами 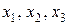 .
.
Ускорение 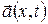 , по определению, есть скорость изменения скорости индивидуальной частицы среды. Поэтому
, по определению, есть скорость изменения скорости индивидуальной частицы среды. Поэтому 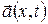 вычисляется как индивидуальная производная по времени. При эйлеровом описании формула для ускорения имеет вид
вычисляется как индивидуальная производная по времени. При эйлеровом описании формула для ускорения имеет вид
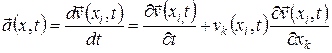 .
.
Лагранжево и эйлерово описания среды эквивалентны: если все интересующие величины заданы в рамках одного из них, то можно найти описание в рамках другого подхода.
Траекторией частицы называется линия, по которой движется частица.
Установившимся, или стационарным, называется движение, при котором в каждой точке пространства, занятого средой, все ее характеристики не меняются со временем, т.е. 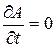 , где А – любая характеристика движения.
, где А – любая характеристика движения.
Задача 1 с решением. Подставить в решение значение q = 2.
Закон движения среды имеет вид
|
|
|
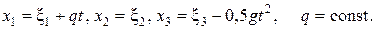
а) Проверьте, что числа (x1, x2, x3) для индивидуальной частицы представляют собой координаты точки пространства в момент времени t=0.
б) Найдите поля скорости и ускорения в лагранжевом описании.
в) Нарисуйте траектории частиц.
г) Является ли это движение установившимся?
Решение
а) найдем координаты точки в момент времени t=0
x1| t=0 =ξ1 +q·0 = ξ1,
x2| t=0 =ξ2 ;
x3| t=0 =ξ3 – 0,5q·0 = ξ3.
Следовательно, числа (x1, x2, x3) для индивидуальной частицы представляют собой координаты точки пространства в момент времени t=0.
б) В декартовой системе координат поле скоростей имеет вид:
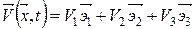
Вычислим компоненты скорости:
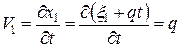
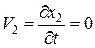
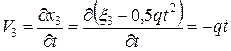
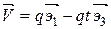 – поле скоростей.
– поле скоростей.
Вычислим компоненты ускорения:
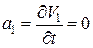 ;
; 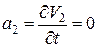 ;
; 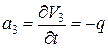
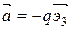 – поле ускорений.
– поле ускорений.
в) Для определения уравнения траектории, примем точку с координатами
(ξ1, ξ2, ξ3) за начало отсчета и совместим с точкой О.
Исключим из уравнений движения время t:
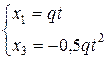 , отсюда
, отсюда 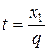
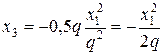 – уравнение параболы, ветви направлены в низ.
– уравнение параболы, ветви направлены в низ.
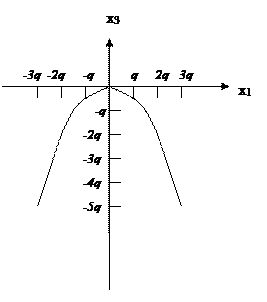
| X1 | - 3q | - 2q | - q | 0 | q | 2q | 3q |
| X3 | - 4,5 q | - 2q | - 0,5 q | 0 | - 0,5 q | - 2q | - 4,5 q |
г) Движение называется установившимся, если в каждой точке пространства, занятого средой, все ее характеристики не меняются со временем, т.е. 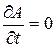 , где А – любая характеристика движения.
, где А – любая характеристика движения.
|
|
|
Т.к. 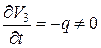 , следовательно, движение является не установившимся.
, следовательно, движение является не установившимся.
Задача 2. Решить по подобию задачи 1. Подставить значение q = 2.
Известен закон движения сплошной среды
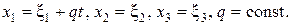
а) Проверьте, что числа (x1, x2, x3) для индивидуальной частицы представляют собой координаты точки пространства в момент времени t=0.
б) Найдите поля скорости и ускорения в лагранжевом описании.
в) Нарисуйте траектории частиц.
г) Является ли это движение установившимся?
2. Тензор напряжений
Силы, действующие на сплошную среду со стороны внешних объектов, можно разделить на две группы: 1) массовые, которые действуют на элемент внутри среды и для малого объема среды пропорциональны массе этого объема; 2) поверхностные, которые приложены к точкам поверхности среды и для малой части поверхности пропорциональны площади этой части.
Поверхностные силы действуют и внутри среды. Действительно, проведем мысленно через любую внутреннюю точку некоторую поверхность. Можно ввести вектор напряжений для любой площадки внутри среды. Он, конечно, будет разным для разных площадок, проведенных через рассматриваемую точку. Ориентацию площадки задают, указывая направление вектора нормали к ней. Вектор напряжений на площадке с нормалью 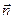 обозначается через
обозначается через 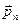 .
.
|
|
|
Итак, вектор напряжений 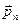 – это предел отношения силы
– это предел отношения силы 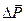 , действующей на площадке с нормалью
, действующей на площадке с нормалью 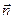 , к ее площади
, к ее площади 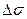 , когда
, когда 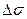 стремится к нулю:
стремится к нулю:
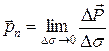 .
.
При этом 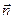 считается направленным в сторону, внешнюю по отношению к части среды, на которую действует рассматриваемая сила
считается направленным в сторону, внешнюю по отношению к части среды, на которую действует рассматриваемая сила 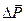 .
.
Помимо скалярных и векторных полей в механике сплошной среды рассматриваются ещё и тензорные поля.
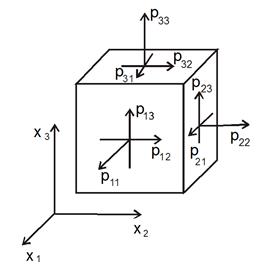
Рис.1 Система напряжений на гранях элементарного объёма
Вырежем в жидкости элементарный параллелепипед с рёбрами dx1, dx2, dx3 (рис.1). На грани этого параллелепипеда со стороны остальной жидкости действуют поверхностные напряжения. В общем случае на каждую грань действуют как нормальные, так и касательные напряжения. В принятой записи каждое из напряжений будет иметь два индекса. Первый индекс означает ориентацию площадки, на которую действует напряжение, второй - ось проектирования.
Рассмотрим векторы напряжений 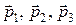 на площадках, перпендикулярных координатным осям декартовой ортогональной системы координат, т.е. на площадках с нормалями
на площадках, перпендикулярных координатным осям декартовой ортогональной системы координат, т.е. на площадках с нормалями 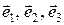 (единичные вектора, направленные по осям X1, X2, X3 соответственно). Компоненты этих векторов обозначаются как
(единичные вектора, направленные по осям X1, X2, X3 соответственно). Компоненты этих векторов обозначаются как 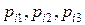 , так что
, так что 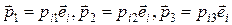 . Введем матрицу, в которой первый столбец состоит из компонент вектора
. Введем матрицу, в которой первый столбец состоит из компонент вектора 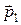 , второй – из компонент вектора
, второй – из компонент вектора 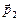 , третий – из компонент вектора
, третий – из компонент вектора 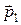 :
:
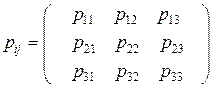 , при i = 1,2,3; j = 1,2,3.
, при i = 1,2,3; j = 1,2,3.
· Первый индекс означает номер строки, второй - номер столбца.
· Нормальные напряжения имеют два одинаковых индекса - диагональ матрицы (p11, p22, p33).
· Касательные напряжения имеют разные индексы (остальные числа в матрице).
Элементы 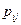 этой матрицы являются компонентами тензора, который называется тензором напряжений Р.
этой матрицы являются компонентами тензора, который называется тензором напряжений Р.
Компоненты напряжений представляют как нормальные, так и касательные напряжения. Касательные напряжения возникают вследствие вязкости, которой обладают все реальные жидкости.
В покоящейся вязкой жидкости:
· касательные напряжения отсутствуют, так как скорости деформации равны нулю,
· нормальные напряжения вызваны только давлением и не зависят от ориентации площадки. (Закон Паскаля).
С помощью закона сохранения количества движения доказывается, что для любой площадки с нормалью 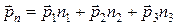 в рассматриваемой точке вектор напряжений
в рассматриваемой точке вектор напряжений 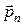 с компонентами
с компонентами 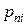 может быть вычислен по формуле (формула Коши)
может быть вычислен по формуле (формула Коши)
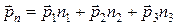 ,
,
где 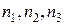 – компоненты вектора
– компоненты вектора 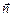 . В проекциях на декартовые координатные оси эта формула записывается в виде
. В проекциях на декартовые координатные оси эта формула записывается в виде
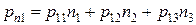 ;
;
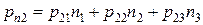 ;
;
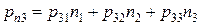
Главные компоненты тензора напряжений P равны 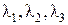 (т.е.
(т.е. 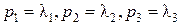 ). Для нахождения главных компонент надо решить кубическое уравнение относительно l:
). Для нахождения главных компонент надо решить кубическое уравнение относительно l:
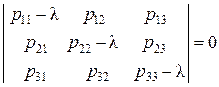 .
.
Задача 3 с решением.
Матрица компонент 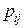 тензора напряжений имеет вид:
тензора напряжений имеет вид:
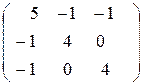 .
. 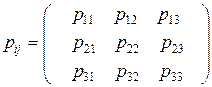
а) Найдите компоненты вектора напряжений 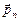 на площадке с нормалью
на площадке с нормалью 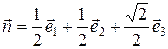 .
.
Вычислите:
б) модуль вектора 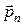 ;
;
в) 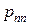 – проекцию вектора
– проекцию вектора 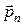 на нормаль
на нормаль 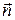 ;
;
г) 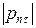 – величину проекции вектора
– величину проекции вектора 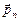 на плоскость площадки (то есть величину касательной составляющей вектора напряжений);
на плоскость площадки (то есть величину касательной составляющей вектора напряжений);
д) угол 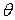 между вектором
между вектором 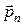 и нормалью к площадке.
и нормалью к площадке.
е) Найдите первый инвариант тензора напряжений.
ж) Найдите главные компоненты тензора напряжений Р.
Решение
а) 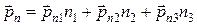 – формула Коши.
– формула Коши.
В проекциях на декартовые оси эта формула записывается в виде:
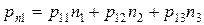 ;
;
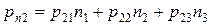 ;
;
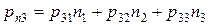
Подставив в эту формулу компоненты вектора нормали 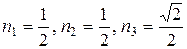 , получаем для компонент вектора напряжений:
, получаем для компонент вектора напряжений:
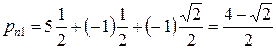
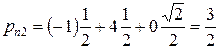
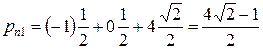
б) Модуль вектора 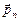 найдем по теореме Пифагора
найдем по теореме Пифагора
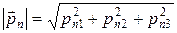 , после подстановки имеем
, после подстановки имеем 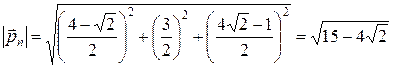
в) 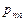 – проекцию вектора
– проекцию вектора 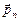 на нормаль
на нормаль 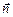 , определим по формуле Коши
, определим по формуле Коши
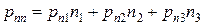 , после подстановки получим
, после подстановки получим
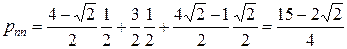
г) 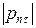 – величину проекции вектора
– величину проекции вектора 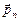 на плоскость площадки (то есть величину касательной составляющей вектора напряжений), найдем по теореме Пифагора
на плоскость площадки (то есть величину касательной составляющей вектора напряжений), найдем по теореме Пифагора 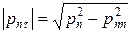 , после подстановки получаем
, после подстановки получаем 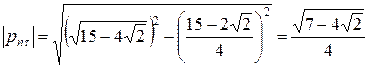
д) Найдем угол 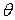 между вектором
между вектором 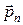 и нормалью к площадке
и нормалью к площадке
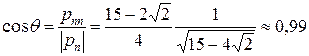
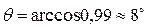
е) Первый инвариант тензора напряжений 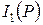 , в декартовых координатах находится по формуле:
, в декартовых координатах находится по формуле: 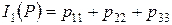 .
.
I 1 ( p ) = 5+4+4=13.
ж) Главные компоненты находятся как корни 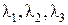 (т.е.
(т.е. 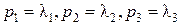 ) следующего кубического уравнения относительно l:
) следующего кубического уравнения относительно l:
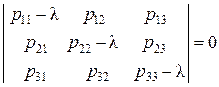 .
.
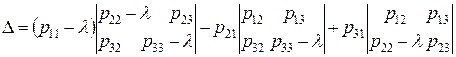 =
=
= (p11-l)(p22-l)(p33-l) – (p11-l)×p23×p32 – p21×p12×(p33-l) + p21×p13×p32 + p31×p12×p23 – p31×p13×(p22-l) =
= (5-λ)(4-λ)(4-λ)-(5-λ)0-(-1)(-1)(4-λ)+(-1)0(-1)+(-1)(-1)0-(-1)(4-λ)(-1) =
= -λ3 + 13λ2 - 54λ + 72
Решим кубическое уравнение
-λ3 + 13λ2 - 54λ + 72 =0
-λ3 + 9λ2 + 4λ2 - 36λ - 18λ + 72 =0
(4-λ)(18-9λ+λ2)=0
4-λ=0
λ1 = 4
λ2 -9λ +18 = 0
D=9, после подстановки находим корни квадратного уравнения λ2 = 6, λ3 = 3.
Получаем главные компоненты тензора напряжений
Р1 = λ1 = 4
Р2 = λ2 = 6,
Р3 = λ3 = 3.
Задача 4. Решить задачу по подобию задачи 3.
Тензор напряжений 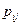
| Уравнение нормали |
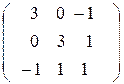
| 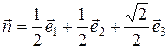
|
а) Найдите компоненты вектора напряжений 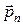 на площадке с заданной нормалью.
на площадке с заданной нормалью.
Вычислите:
б) модуль вектора 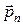 ;
;
в) 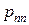 – проекцию вектора
– проекцию вектора 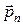 на нормаль
на нормаль 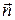 ;
;
г) 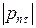 – величину проекции вектора
– величину проекции вектора 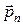 на плоскость площадки (то есть величину касательной составляющей вектора напряжений);
на плоскость площадки (то есть величину касательной составляющей вектора напряжений);
д) угол 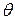 между вектором
между вектором 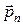 и нормалью к площадке.
и нормалью к площадке.
е) Найдите первый инвариант тензора напряжений.
ж) Найдите главные компоненты тензора напряжений P.
Дата добавления: 2019-07-15; просмотров: 961; Мы поможем в написании вашей работы! |

Мы поможем в написании ваших работ!
