Вывод дифференциальных уравнений движения жидкости и газа в трещиноватых и трещиновато-пористых средах

XI. ОСНОВЫ ТЕОРИИ ФИЛЬРАЦИИ В ТРЕЩИНОВАТЫХ И ТРЕЩИНОВАТО-ПОРИСТЫХ СРЕДАХ

Особенности фильтрации в трещиноватых

И трещиновато-пористых средах

Промысловые данные, а также данные исследования кернов и шлифов свидетельствуют о том, что трещиноватые породы имеют сложную систему строения, а движение в них жидкости и газа отличается некоторыми особенностями по сравнению с движением в пористой среде. В трещиноватой породе имеются микро- и макротрещины, мелкие и крупные каверны, полости; сама порода — матрица (пространство между трещинами) может быть абсолютно непроницаемой или представлять собой обычную пористую среду. Раскрытия макротрещин имеют порядок 1 мм, а в отдельных случаях и больше, микротрещин – 1-100 мкм. Исходя из того, что сопротивление движению жидкости в трещиноватых породах достаточно велико, исследователи считают, что макротрещины не имеют значительной протяженности и в большинстве случаев соединяются между собой микротрещинами (которые и создают большие сопротивления).

Для понимания особенностей фильтрации жидкости и газа в трещиноватых породах рассматривают две модели пород — чисто трещиноватые и трещиновато-пористые (рис.78). В чисто трещиноватых породах (см. рис. 78,а) блоки породы, расположенные между трещинами, практически непроницаемы, движение жидкости и газа происходит только по трещинам (на рисунке показано стрелками), т. е. трещины являются и коллектором, и проводником жидкости к скважинам. К таким породам относятся сланцы, кристаллические породы, доломиты, мергели и некоторые известняки. Рассматривая трещиноватую породу с жидкостью как сплошную среду, нужно за элемент породы принимать

Рис. 78. Схемы чисто трещиноватой (а) и трещиновато-пористой (б) сред: 1,3 – трещины; 2-пористые блоки

объем, содержащий большое количество блоков, и усреднение фильтрационных характеристик проводить в пределах этого элемента, т. е. масштаб должен быть гораздо большим, чем в пористой среде. Если представить себе блок в виде куба со стороной а= 0,1 м, то в качестве элементарного объема надо взять куб со стороной порядка 1 м.

Трещиновато-пористая среда представляет собой совокупность пористых блоков, отделенных один от другого развитой системой трещин (см. рис.78,б). Жидкость или газ насыщают и проницаемые блоки, и трещины. При этом поперечные размеры трещин значительно превосходят характерные размеры пор, так что проницаемость системы трещин k₁ значительно больше, чем проницаемость системы пор в блоках k₂. В то же время трещины занимают гораздо меньший объем, чем поры, так что коэффициент трещиноватости m₁- отношение объема, занятого трещинами, к общему объему породы, существенно меньше пористости отдельных блоков m₂.

Трещиновато-пористые коллекторы — это в основном известняки, иногда песчаники, алевролиты, доломиты.

Рис. 79. Модель трещиноватой среды с упорядоченной системой трещин

Рассмотрим характеристики чисто трещиноватой породы. Трещина представляет собой узкую щель, два измерения которой во много раз больше третьего. Коэффициент трещиноватости составляет обычно доли процента (в то время, как коэффициент пористости зернистой породы составляет 10—20%). Коэффициент трещиноватости m₁ так же, как и коэффициент проницаемости k₁, определяется густотой и раскрытием трещин. Густотой трещин Г называется число трещин п, отнесенное к длине нормали L, проведенной к поверхностям, образующим трещины. Для простоты представим себе модель трещиноватой среды с упорядоченной системой параллельных и равноотстоящих трещин с раскрытием d(рис. 79). Густота трещин Г = п/ h , а коэффициент трещиноватости

(11.1)

Движение жидкости или газа в трещине можно представить себе как движение в узкой щели между двумя параллельными плоскими стенками с расстоянием между ними d; для такого движения справедлива формула Буссинеска, согласно которой средняя скорость движения жидкости в щели

(11.2)

где m - динамический коэффициент вязкости; 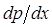- градиент давления.

Переходя к скорости фильтрации , получим

(11.3)

Сопоставив формулу (11.3) с законом Дарси, найдем выражение для коэффициента проницаемости трещиноватой породы.

(11.4)

Экспериментами установлена зависимость проницаемости трещиноватых пород от пластового давления более существенная, чем зависимость от давления проницаемости пористых сред. Из формулы (11.4) зависимость k₁(p) можно получить следующим образом. Горное давление, которое можно считать постоянным, уравновешивается напряжениями в скелете породы и давлением жидкости в трещинах. При снижении пластового давления увеличивается нагрузка на скелет породы и уменьшается раскрытие трещин (с ростом давления раскрытие трещин увеличивается). Если считать, что деформации в трещиноватом пласте упругие и малы по величине, то зависимость раскрытия трещины от давления можно считать линейной:

, (11.5)

где b - параметр трещиноватой среды, зависящий от упругих свойств и геометрии трещин. Исходя из формул (11.4) и (11.5), можно записать зависимость коэффициента проницаемости k₁ от давления следующим образом:

(11.6)

где - коэффициент проницаемости трещиноватой породы при давлении p₀.

Как уже указывалось ранее, экспериментом хорошо подтверждается экспоненциальная зависимость проницаемости от давления:

(11.7)

а при малых изменениях давления зависимость можно считать линейной:

, (11.8)

где .

При рассмотрении установившейся фильтрации в трещиновато-пористом пласте обычно считают, что коэффициент проницаемости трещин k₁ существенно зависит от давления и определяется одной из формул (11.6) –(11.8), а коэффициент проницаемости пористых блоков k₂ не зависит от давления и принимается постоянным. Соотношения для установившихся фильтрационных потоков в трещиновато-пористой среде получаются суммированием потоков в трещинах и в пористых блоках.

В трещиноватых породах, где истинное сечение потока сравнительно мало, а дебиты обычно велики, особенно вероятно отклонение от закона Дарси за счет проявления инерционных сил. При этом обычно используют двучленный закон фильтрации (1.23).

Наиболее ярко особенности фильтрации в трещиновато-пористой среде проявляются в неустановившихся процессах. Система трещин и система пор представляют собой две среды с разными масштабами (см. рис. 78,б). Средний размер пор составляет 1—100 мкм, протяженность трещин — от нескольких сантиметров до десятков метров. Так как коэффициент пористости блоков m₂ на один-два порядка выше, чем коэффициент трещиноватости m₁, то большая часть жидкости находится в порах. Чаще всего пористые блоки малопроницаемы ( ) и жидкость, фильтруясь из них в трещины, движется в скважины в основном по трещинам, проводимость которых значительно выше, чем пористых блоков.

Рассмотрим этот процесс подробнее. Пусть происходит резкое изменение давления на забое скважины. Если блоки считать непроницаемыми, то можно использовать обычную теорию упругого режима, причем коэффициент пьезопроводности , определенный через характеристики системы трещин, может оказаться очень большим, так как k₁ велик, а m₁ мал. Это значит, что процесс перераспределения давления в трещинах будет происходить с большой скоростью и в трещинах за сравнительно небольшое время установится новое распределение давления. Из-за малой проницаемости блоков k₂ жидкость из них выходит медленно и давление в блоках длительное время сохраняет свое начальное значение. Тем самым между жидкостью, находящейся в блоке, и жидкостью, его окружающей, создается разность давлений. В результате перетока части жидкости из блока в трещины происходит постепенное выравнивание давлений. Этот процесс будет тем длительнее, чем меньше проницаемость блока k₂, больше его размеры, пористость m₂, сжимаемость жидкости b_Ж и порового пространства b_C.

Таким образом, характеристики движения в блоках и трещинах оказываются различными: давление в блоках p₂ больше, чем давление в трещинах p₁, скорость фильтрации в блоках V₂ значительно меньше, чем в трещинах V₁. Поэтому трещиновато-пористую среду рассматривают как совмещение двух пористых сред с порами разных масштабов: 1) среда 1 — укрупненная среда, в которой роль зерен играют пористые блоки, которые рассматриваются как непроницаемые, а роль поровых каналов — трещины, давление в этой среде равно p₁, скорость фильтрации V₁; 2) среда 2 — система пористых блоков, состоящих из зерен, разделенных мелкими порами, давление в ней достигает p₂, скорость фильтрации V₂ . Таким образом, p₁- среднее давление в трещинах в окрестности данной точки, p₂ - среднее давление в блоках, аналогично для скоростей фильтрации.

Важная особенность неустановившейся фильтрации в трещиновато-пористой среде — интенсивный обмен жидкостью между обеими средами, т. е. между пористыми блоками и трещинами, обусловленный различием давлений в этих средах p₁ и p₂. Обмен жидкостью происходит при достаточно медленном изменении давлений с течением времени, поэтому этот процесс можно считать квазистационарным, т. е. не зависящим явно от времени. Очевидно, что при движении слабосжимаемой жидкости масса жидкости, вытекающей из блоков в трещины за единицу времени в единице объема породы (интенсивность перетока q), пропорциональна разности давлений p₂-p₁, плотности 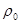(считая, что плотность мало изменяется в интервале давлений от p₁ до p₂) и обратно пропорциональна вязкости m, т. е.

(11.9)

где a₀ — безразмерный коэффициент, зависящий от геометрических характеристик блоков: проницаемости k₂, среднего размера блоков и безразмерных величин, характеризующих форму блоков;

Соотношение (11.9) должно быть уточнено для случая, если плотность значительно зависит от давления. Например, при фильтрации идеального газа интенсивность перетоков из блоков в трещины представляется в виде

(11.10)

где p₀ —фиксированное давление, соответствующее плотности .

Вывод дифференциальных уравнений движения жидкости и газа в трещиноватых и трещиновато-пористых средах

Выведем дифференциальные уравнения движения жидкости и газа в деформируемой трещиновато-пористой среде, считая, что в каждой точке имеется два давления (p₁— в системе трещин, p₂ — в пористых блоках) и две скорости фильтрации —V₁ и V₂ соответственно. Перетоки между средами определяются формулами (11.9) или(11.10).

При составлении дифференциальных уравнений записывают два уравнения неразрывности — одно для фильтрации в трещинах (среда 1), другое для фильтрации в пористых блоках (среда 2). Уравнение баланса жидкости в трещинах, т. е. уравнение неразрывности, отличается от уравнения (2.11) только наличием в правой части добавочного члена, представляющего собой массу жидкости (или газа) q, перетекающей за единицу времени из блоков в трещины в единице объема среды:

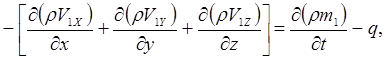(11.11)

где — плотность жидкости или газа при давлении p₁.

Для фильтрации в пористых блоках уравнение неразрывности принимает вид

(11.12)

где — плотность жидкости или газа при давлении p₂.

Для чисто трещиноватого пласта q = 0 и остается только уравнение (11.11), так как в блоках не содержится жидкости.

Считая, что выполняется линейный закон Дарси, можем написать дифференциальные уравнения движения в системе трещин и в пористых блоках соответственно:

(11.13)

(11.14)

К уравнениям (11.11)—(11-14) должны быть добавлены зависимости плотности , пористостей обеих сред m₁ и m₂ и проницаемостей k₁ и k₂ от давлений p₁ и p₂.

Подставив выражения (11.13), (11.14), а также (11.9) для упругой жидкости или (11.10) для газа в уравнения неразрывности (11.11) и (11.12), получим систему уравнений неустановившейся фильтрации любого однородного флюида в трещиновато-пористой среде в общем виде

(11.15)

(11.16)

где 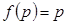— для упругой жидкости; — для идеального газа.

Для получения единственного решения при интегрировании этой системы дифференциальных уравнений в частных производных относительно давлений p₁ и p₂ к ней необходимо добавить начальные и граничные условия.

Дата добавления: 2019-07-15; просмотров: 565; Мы поможем в написании вашей работы!

Поделиться с друзьями:

12 3 Следующая ⇒

Мы поможем в написании ваших работ!