Спектры некоторых периодических последовательностей

ЛЕКЦИЯ 1

СИГНАЛЫ

Основные определения

Теория передачи сигналов посвящена исследованию основных процессов в создании информации, ее электрическому отображению, преобразованию и передаче сигналов, представляющих полезную информацию. Иногда теорию передачи сигналов (ТПС) называют "общей теорией связи", что лишний раз подчеркивает назначение и применение выводов этой теории. ТПС содержит разделы: основы теории информации, теорию кодирования, теорию модуляции сигналов, основы помехоустойчивой обработки принимаемых сигналов. Под информацией понимают некоторые сведения о событиях или материальных системах. Формы представления информации, называемые сообщением, имеют разнообразный вид: текст, речь, данные на выходе ЭВМ, телевизионное изображение и т.д.

Физический процесс, переносящий информацию, называется сигналом. С информационной точки зрения сигналы можно разделить на детерминированные и случайные.

Детерминированный сигнал – такой сигнал, мгновенные значения которого в любой момент времени можно предсказать с вероятностью единица.

Периодический сигнал – это сигнал, любое значение которого повторяется через период Т, т.е. S(t) = S(t+T). -∞<t<∞.

Непериодический сигнал – сигнал, не подчиняющийся условию периодичности.

Случайный сигнал – такой сигнал, мгновенные значения которого заранее неизвестны и могут быть предсказаны лишь с некоторой вероятностью (сигналы речи, музыки, телеграфного кода). По существу, любой сигнал, несущий информацию, должен рассматриваться как случайный.

Параметры детерминированных сигналов:

1) Мгновенное значение сигнала (в заданный момент времени)
S* = S(t*); t* - заданный момент.

2) Максимальное значение сигнала - наибольшее мгновенное значение сигнала на протяжении заданного интервала времени: S_max = max S(t);
T* = t₂ – t₁ – заданный интервал времени.

 

Рис. 1.1.

 

3) Минимальное значение сигнала – наименьшее мгновенное значение в заданном интервале времени: S_min = min S(t); T* = t₂ – t₁/

4) Постоянная составляющая сигнала (среднее значение)

.

5) Переменная составляющая сигнала:

.

6) Наиболее пиковое значение сигнала – наибольшее мгновенное значение переменной составляющей сигнала: S_~max.

7) Наименьшее пиковое значение сигнала – наименьшее мгновенное значение переменной составляющей сигнала: S_~min.

8) Размах сигнала R = S_max – S_min.

9) Средневыпрямленное значение сигнала (среднее значение модуля сигнала): . Кстати, большинство измерительных приборов (напряжения) измеряют средневыпрямленное значение и градуированы по синусоидному сигналу. Если сигнал не синусоидальный (искаженный) или случайный, нужно измерять напряжение по среднеквадратичному значению.

10) Среднеквадратичное значение сигнала: .

11) Период и частота повторения периодичного сигнала: ; ; Т = Т_повт.

12) амплитуда периодического сигнала – максимальное значение переменной составляющей периодического сигнала A(S) = max|S(t)|.

13) Длительность импульсного сигнала – длительность импульса на уровне 0,1А.

 

 

Рис. 1.2

 

14) Длительность фронта импульса t_ф – время нарастания (спадания) уровня импульса от 0,1 до 0,9А (амплитуды).

15) Скалывание вершины импульса С_k – величина спада вершины импульса за время его длительности.

16) Скважность импульсной последовательности Q – отношение периода повторения к длительности импульса Q = T/τ_и.

17) "Пачка" импульсов – несколько одинаковых импульсов, объединенных в пачку с общими (одинаковыми) параметрами.

18) Энергия сигнала на интервале t₂, t₁:

.

19) Средняя мощность на интервале t₂, t₁:

 

Литература:

[1] стр. 5-10; 17-23. [2] стр. 10-13; 29-36. [3] стр. 7-10.

 

Контрольные вопросы:

1. Что такое детерминированный сигнал?

2. Каковы условия периодического сигнала?

3. Что такое скважность импульсной последовательности?

4. Каковы параметры импульсного сигнала?

5. Что такое "пачка" импульсов?

 

Спектральный анализ сигналов

Любая временная функция – сигнал x(t) может быть представлена набором простейших функций (подобно разложению числа на сомножители). Главное требование к простейшим функциям – их единственность (уникальность) и непохожесть на другие функции. Это свойство исключительности набора простейших функций отражается в математике свойством ортогональности: (на некотором интервале (0,Т)):

.

Разложение на простейшие функции представляется рядом:

.

Коэффициенты ряда – С_k выбираются из условия минимума среднеквадратичной погрешности по отношению к исходному сигналу:

и находится по формуле (с учетом нормировки)

.

При увеличении членов ряда n к бесконечности (∞) погрешность отображения исходной функции x(t) становится сколь угодно малой. Тогда такой ряд называют обобщенным рядом Фурье.

В качестве простейших ортогональных функций часто выбирают тригонометрический ряд:

.                            (1.1)

Совокупность коэффициентов ряда {C_k} называют спектром амплитуд или амплитудно-частотным спектром, а совокупность {j_k} - спектром фаз или фазово-частотным спектром. С учетом:

              (1.2)

и

   

получаем другую форму ряда Фурье:

,              (1.3)

где коэффициенты a_k и b_k определяется как:

; ; . (1.4)

Разложение сигнальной функции на "простейшие" составляющие называют спектральным анализом или спектральным разложением. В тригонометрическом ряде Фурье в качестве "простейшей" функции принято синусоидальное (косинусоидальное) колебание одной частоты, называемое "гармоническим". Поэтому составляющие ряда Фурье называют "гармоники"; имея в виду, что ряд состоит из кратных -k- частот, т.е. кратных гармоник (первая гармоника, вторая гармоника … сотая гармоника …). Так как интервал ортогональности 0,Т – совпадает с периодом Т = 2p/w₁, то определение коэффициентов ряда производится в пределах интервала ортогональности (-Т/2, Т/2).

Коэффициенты a_k называют косинусной (четной) составляющей, b_k - синусной (нечетной).

Рассмотрим пример спектрального разложения периодического колебания типа "меандр". Меандр – греческое слово, обозначающее "орнамент" (рис. 1.3).

 

 

 

 

а)                                          б)

Рис 1.3

  .

Выбор начала координат а) или б) определит состав гармонического разложения: по четным коэффициентам или не четным, это определяется видом функций x(t) в пределах (-Т/2, Т/2). В случае выбора начала координат по а) функция x(t) оказывается нечетной, т.е. х(-Т/2) = -х(Т/2), при этом в ряде Фурье остаются только члены b_k, определяемые нечетной функций синуса. Составляющие a_k оказываются при этом, равными нулю a_k = 0. В случае выбора начала координат по б) функция x(t) оказывается четной, и ряд Фурье будет определяться только составляющими a_k, b_k = 0. Постоянная составляющая, как видно из графика, равна нулю. Для случая а):

с учетом, что  и

.

Тогда ряд Фурье:

или с учетом w = 2πf

.      (1.5)

Полученный спектральный состав можно представить графически (рис. 1.4).

 

Рис. 1.4

 

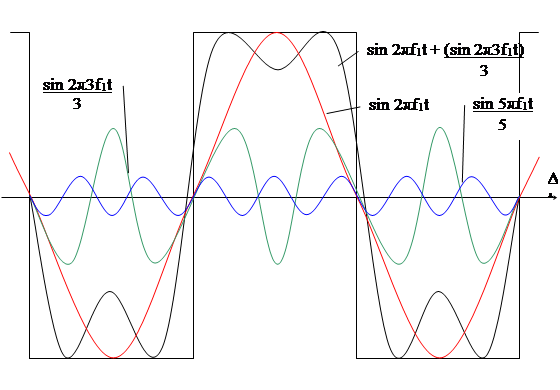Приведенный график называют "спектром". Синтез исходной временной функции по спектральным составляющим понятен из рис. 1.5.

 

 

Рис. 1.5

Спектры некоторых периодических последовательностей

Спектральный состав периодической последовательности прямоугольных видеоимпульсов.

 

 

Рис. 1.6

 

,

где T_n – период повторения; Е – амплитуда импульса; t_u – длительность.

Отношения: Q = T_n/t_u – называется "скважностью".

Определим спектральный состав бесконечной последовательности видеоимпульсов. Находим постоянную составляющую:

Так как функция x(t) в пределах t_u – четная, то необходимо искать гармонические составляющие – a_k (b_k = 0).

Тогда ряд Фурье будет:

.  (1.6)

Исследуем полученное выражение. Здесь текущее, непрерывное значение имеет только сомножитель coskw₁t, тогда все остальные сомножители представляют численное выражение для спектральных составляющих, кратных w₁ = 2p/Т. Выражение в квадратных скобках – это число – численное значение гармонических составляющих, причем выражение  - представляет собой по переменной
k – функцию sinc x = (sin x)/x и соответствует огибающей гармонического ряда, она обращается в нуль в точках частоты, которые можно найти из условия:  что возможно, если wt_u/2 = p, откуда wt_u = 2p и
w = 2p/t_u тогда графическое отображение ряда Фурье будет (рис. 1.7):

 

 

Рис. 1.7

 

Итак, спектральное разложение последовательности видеоимпульсов состоит из суммы дискретных гармонических составляющих, кратных 2p/Т, причем знак гармоник в разных "лепестках" графика отличается на 180°, что демонстрирует изменение их фазы на p и создает фазовый спектр.

С учетом разделения общего спектра на амплитудно-частотный и фазово-частотный графики спектрального разложения можно изобразить иначе (а также учтем, что w = 2pf и перейдем к герцовой частоте – f):

 

а)

 

 

б)

 

 

Рис. 1.8

 

Обычно фазовочастотным спектром (рис. 1.8б) не интересуются (его опускают) и исследуют, в основном, амплитудно-частотный спектр, который жаргонно называют просто "спектр" (рис. 1.8а).

Рассмотрим влияние параметров последовательности видеоимпульсов на показатели амплитудного спектра. Сначала изменим длительность импульса. При увеличении длительности импульса (t_u2 = 2t_u1) спектр "сжимается" вдвое, при укорочении длительности (t_u3 = 0,5t_u1) спектр "расширяется" вдвое.

 

 

 

Рис. 1.9

 

Если в пределе длительность импульса устремить к нулю t_u ® 0 (это принятый в математике единичный импульс, у которого длительность
t_u ® 0, а площадь остается равной единице S = 1, обозначают этот импульс d(t₀) – дельта-импульс), то спектральный состав первого лепестка спектра импульса расширяется до бесконечности, превращаясь в равномерный спектр от 0 до ¥ со спектральной плотностью G₀.

 

 

Рис. 1.10

 

С другой стороны, при увеличении длительности импульса в пределе до бесконечности t_u ® ¥, получаем просто постоянный ток, спектральный состав которого выражается в одно единственное значение на частоте
w = 0, т.е. значение постоянной составляющей.

Теперь, не меняя длительности импульсов, будем изменять период повторения.

Увеличим период вдвое, количество спектральных составляющих увеличится также вдвое, а расстояние по частоте сократится вдвое.

 

 

Рис. 1.11

 

Уменьшения периода повторения приводит к увеличению расстояния между дискретными гармониками. Уменьшим период повторения до величины Т = 2t_u, что приводит к колебанию типа "меандр" и построим для него спектр.

 

 

Рис. 1.12

 

Получаем спектр, состоящий из нечетных гармоник (четные гармоники приходятся на нули огибающей спектра), т.е. получаем уже найденный выше спектр другим путем (см. рис. 1.4).

Теперь устремим период повторения видеоимпульсов в ¥, т.е. приходим к понятию единичного импульса. Спектральные составляющие постепенно сближаются и в пределе сливаются в сплошной спектр, который будет характеризоваться спектральной плотностью, т.е. энергией спектра, приходящейся на элемент текущего значения частоты df.

Спектральный состав одиночного импульса вырождается в функцию:

.              (1.7)

 

 

Рис. 1.13

 

При этом ряд Фурье переходит в интеграл, и получаем прямое и обратное преобразование Фурье:

;      .  (1.8)

Рассмотрим, теперь, ситуацию когда последовательность видеоимпульсов ограничена, т.е. сигнал выглядит в виде "пачки" импульсов с параметрами: количество импульсов – n, длительность одного импульса - t_u, период повторения – Т, D – длина "пачки" nT+t_u.

 

 

Рис. 1.14

 

Строим спектр "пачки" последовательно, сначала определим самый протяженный по частоте элемент спектра, он определяется самым коротким во времени элементов – самим импульсом с длительностью t_u. Затем примем, что последовательность импульсов бесконечна и в соответствии с предыдущим анализом бесконечной последовательности определим дискретные составляющие спектра, расположенные на расстояниях по частоте Df = 1/Т (рис. 1.16).

 

Рис. 1.15

 

Рис. 1.16

После этого рассмотрим спектр "пачки" импульсов, принимая длительность всей пачки за одиночный видеоимпульс, совмещая все приведенные рассуждения в единую систему, строим спектральную характеристику "пачки" видеоимпульсов.

 

Рис. 1.17

 

 

Рис. 1.18

 

И, наконец, рассмотрим спектральное разложение радиоимпульсов, который отличается от видеоимпульса наличием заполнения несущим гармоническим колебанием частотой f₀ внутри импульса. Теперь видеоимпульс играет роль огибающей для радиоимпульса:

.

 

 

 

Рис. 1.19

 

В соответствии с теоремой переноса спектра: S₂(w₀) = S₁(w₀ -w)

 

 

Рис. 1.20

 

Имея в виду, что преобразование Фурье действует в пределах от
w = -¥ до w = +¥ (а мы исследуем только область положительных частот спектра, удваивая его энергию за счет несуществующей "отрицательной" полосы), спектр, перенесенный на несущее колебания с частотой - w₀ занимает область и справа и слева от значения несущей, как и следует из математически точного расчета спектра. Полоса занимаемых частот при этом удваивается.

 

Литература:

[1] стр. 42-48. [2] стр. 36-44. [3] стр. 36-45.

Контрольные вопросы:

1. Какая разница между амплитудным спектром и фазовым?

2. Какое отличие спектра периодического сигнала от непериодического?

3. Чем отличается спектр радиосигнала от спектра видеосигнала?

4. В чем особенности спектра ограниченной "пачки" сигналов?

 

Теорема Котельникова

Любой непрерывный сигнал может быть представлен отдельными дискретными отсчетами, определенными в соответствии с теоремой Котельникова. Непрерывный сигнал, ограниченный спектром 0-F_в
(рис. 1.21) может быть представлен дискретными отсчетами, взятыми с интервалом

,                                            (1.9)

где F_в – верхняя частота в спектре сигнала.

 

 

Рис. 1.21                                      Рис. 1.22

 

Процесс замены непрерывного сигнала на дискретные отсчеты называется дискретизацией. Величина, обратная интервалу дискретизации
f_д = 1/∆t называется частотой дискретизации. Теорема Котельникова может иметь другое условие: f_д ≥ 2F_в – частота дискретизации должна быть как минимум вдвое выше верхней частоты спектра сигнала.

Если спектр сигнала находится в полосе частот ∆F = f_в - f_н, не включая нулевых частот, то правило дискретизации Котельникова выглядит так: f_д ≥ 2∆F.

Термин "может быть представлен" подразумевает полное (без потери информации) восстановление сигнала по его дискретам не только в точках дискретных отсчетов, но и в любой другой точке. С этой целью Котельников предложил специальный ряд:

 sinc 2πF_в(t-k∆t),                        (1.10)

здесь k – порядковый номер дискретного отсчета;

sinc x – специфическая функция вида:

sinc х = ,                                     (1.11)

где .

Sinc х представляет собой затухающую периодическую функцию. Особо следует отметить значение этой функции в точке 0.  устанавливает неопределенность, которая раскрывается по правилу Лапиталя.

.

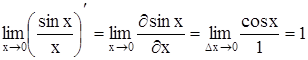Ряд Котельникова имеет специфическую функцию sinc x, при которой он зависит только от своего отсчета и не влияет на другие отсчеты, так как проходит через значения 0 в моменты других отсчетов. В точке х необходимо просуммировать отрезки от всех функций ряда и получить по отсчетам исходное значение непрерывной функции R (рис. 1.24).

 

 

Рис. 1.23

 

Рис. 1.24

 

Восстановление непрерывного сигнала будет тем точнее, чем больше функций отсчетов будет привлечено к формированию значения искомой точки R. Для повышения качества отсчета (минимума возможной ошибки) желательно брать отсчеты чаще, т.е. уменьшать ∆t (или что тоже самое увеличивать частоту дискретизации f_д↑).

Дискретное представление сигналов позволяет использовать его для временного уплотнения канала связи, в промежуток времени между дискретными отсчетами можно поместить дискретные отсчеты другого сигнала.

Такой принцип уплотнения называется ВРК – временное разделение каналов.

Период дискретизации здесь одинаков для каждого сигнала (канала), а отсчеты сдвинуты по времени.

 

Рис. 1.25

 

Реальный дискретный отсчет имеет протяженность и представляет прямоугольный импульс. При прохождении импульса через реальную линию, обладающую потерями в виде приведенной RC – эквивалентной схемы, дискретный импульсный сигнал претерпевает временные искажения ("затягивания"), что может привести к попаданию части энергии сигнала одного канала в другой канал. Это явление называют "внятными переходными помехами". Для снижения этих помех надо, во-первых, улучшать канал (снижать потери) и, во-вторых, желательно увеличить временное расстояние между отсчетами - ∆t (или, что тоже самое, уменьшать частоту дискреции f_д↓).

 

              Рис. 1.26                                      Рис. 1.27

 

 

Рис. 1.28

 

В результате мы приходит к противоречию: с одной стороны для увеличения качества восстановления дискретизированного сигнала необходимо частоту дискретизации увеличивать f_д↑, с другой, для уменьшения взаимного влияния каналов в плохой линии нужно частоту дискретизации уменьшать f_д↓. Для дискретизации телефонного канала с полосой частот 0,3÷3,4 кГц, т.е. ∆F = 3,1 кГц по теореме Котельникова следует взять частоту дискретизации f_д≥2∆F≥6,2 кГц. По рекомендации МККТТ приняты международные нормы, по которым частота дискретизации определена в f_д = 8 кГц.

 

Литература:

[1] стр. 50-54. [2] стр. 44-49. [3] стр. 64-70.

 

Контрольные вопросы:

1. Какие ограничения существуют для дискретного представления сигналов?

2. Запишите ряд Котельникова и поясните физическую сущность членов ряда.

3. Какие условия необходимо соблюсти для полного восстановления непрерывного сигнала?

4. На каких принципах основана система с временным разделением сигналов?

5. Как выбрать частоту дискретизации для целей временного разделения каналов?

 

---

Дата добавления: 2019-07-15; просмотров: 1319; Мы поможем в написании вашей работы!

Поделиться с друзьями:

---

---

Мы поможем в написании ваших работ!