Применение спектрального метода для решения обратных задач динами
Рассмотрим решение спектральным методом обратной задачи динамики в следующей постановке.
Известна система автоматического управления (регулирования), которая может быть как стационарной, так и нестационарной, и работа которой описывается следующим дифференциальным уравнением:
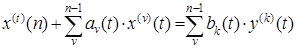(2.1)
где
- сигнал на выходе системы;
- сигнал на входе системы;
- коэффициенты дифференциального уравнения, являющиеся функциями времени.
При этом неизвестны некоторые параметры настройки системы управления, которые необходимо определить в процессе решения задачи. Обозначим множество этих параметров через 
где 
- их число. Тогда коэффициенты дифференциального уравнения будут зависеть от 
и, следовательно можно записать;
(2.2)
Задан эталонный сигнал 
на интервале 
или его спектральная характеристика, который необходимо получить на выходе системы (2.2). В общем случае могут быть заданы ненулевые начальные условия:
(2.3)
Для заданных дифференциального уравнения (2.2), эталонного выходного сигнала и начальных условий (2.3) необходимо определить входной сигнал и искомые сигнала на выходе получили бы сигнал, максимально параметры настройки 
такими, что при подачи на вход системы автоматического управления найденного входного в известном смысле приближенный к эталонному.
В качестве меры близости реального сигнала на выходе системы (2.2), (2.3) к эталонному сигналу 
на интервале примем следующий функционал
|
|
|
(2.4)
Неизвестный входной сигнал будем искать в форме его спектрального разложения в ряд по некоторому базису ортонормированных функций 
;
где коэффициенты 
, неизвестны и их необходимо определить.
Следовательно входной сигнал будет зависеть от времени 
и от множества параметров 
Тогда дифференциальное уравнение (2.2) можно записать в следующей виде
(2.5)
Интегрируя уравнение 
раз с учетом начальных условий, получим
(2.6)
Воспользовавшись справедливым для любой непрерывной функции тождеством
равенство (2.6) можно переписать в виде
(2.7)
Интегрируя полученное равенство (2.7) по частям и применяя формулы
получим
(2.8)
где
Уравнение (2.8) представляет собой уравнение Вольтера 2-го рода. Преобразуем его к интегральному уравнению Фредгольма 2-го рода на интервале исследования 
:
(2.9)
где
Таким образом, получены две эквивалентные формы описания системы: дифференциальное уравнение (2.2) с начальными условиями (2.3) и интегральное уравнение (2.9). Функция 
в выражении (2.9) представляет собой полином, коэффициенты которого зависят от начальных условий (2.3) и от множества 
искомых параметров настройки системы автоматического управления (регулирования). Перепишем 
, изменив порядок суммирования
|
|
|
Введем следующие обозначения:
Тогда полином можно записать следующим образом
где 
- вектор-столбец начальных условий; 
- вектор-столбец полиномов 
.
Рассмотрим левую часть уравнения (2.9). Представим функции, входящие в нее, в виде разложений в ряд по ортонормированному базису 
.
Имеем
, (2.10)
где 
- спектральная характеристика выходного сигнала 
, элементы которой определяются из соотношения
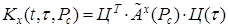(2.11)
где 
- квадратная матрица размерностью 
, элементы которой определяются из выражения
Подставив полученные разложения (2.10) и (2.11) в левую часть уравнения (2.9) и учитывая, что 
, где 
- единичная, в силу ортонормированности базисных функций, получим
(2.12)
где 
- матрица спектральной характеристики инерционной части системы размерностью 
.
Сделаем аналогичные преобразования для правой части уравнения (2.9).
, (2.13)
где 
- спектральная характеристика сигнала на входе системы, элементы которой определяются из соотношения
|
|
|
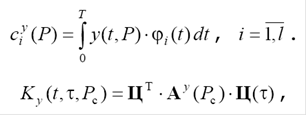(2.14)
где 
- квадратная матрица размерностью 
спектральной характеристики форсирующей части системы, элементы которой определяются из выражения
(2.15)
где 
- матрица размерностью 
элементы которой определяются из соотношения
Подставляя разложения (2.13), (2.14) и (2.15) в (2.9) и делая соответствующие преобразования, получим
(2.16)
Таким образом, уравнение (2.9) с учетом (2.12) и (2.16) можно переписать в следующем виде
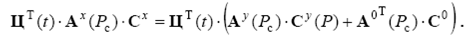(2.17)
Рассмотрим теперь функционал (2.4). Имеем
Так как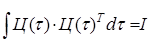 
, то последние выражение можно записать в следующем виде
(2.18)
или
где
. (2.19)
Здесь спектральная характеристика эталонного сигнала 
или задана или, в случае задании эталонного сигнала 
, определяется из выражения
, 
.
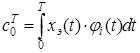Таким образом, задача определения входного сигнала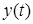 
(точнее множества 
) и множества 
неизвестных параметров настройки системы управления (2.2), (2.3) сводиться к задаче безусловной минимизации функционала (2.18) по элементам множеств и 
, т.е.
.
Практическая часть
Результаты расчётов:
Интервал исследования
tmin = 0.000000e+000, c;
tmax = 7.000000e+000, c;
|
|
|
Nt = 512;
Дата добавления: 2019-07-15; просмотров: 135; Мы поможем в написании вашей работы! |
Мы поможем в написании ваших работ!