Гмурман В.Е., Теория вероятности и математическая статистика. Учебное пособие для вузов. – 8-е издание, 2002г.

Областное коммунальное

Высшее учебное заведение ИП "Стратегия"

Кафедра экономической кибернетики

 

 

Курсовая работа

По дисциплине: "Теория вероятности и математическая статистика".

На тему: Метод экспертных оценок в анализе качества обучающего процесса в ИП "Стратегия"

Выполнила:

Студентка группы М-05-51

Упениекс Анна

Проверила:

Литвинова О.Б.

 

 

Г. Желтые Воды

2006 год

Содержание

 

Введение

1. Ранжирование

2. Конкордация

3. Ранжирование с совпавшими рангами

Практическая работа

Вывод

 

Введение

 

При решении экономических и производственных задач часто приходится сталкиваться с необходимостью формализации систем, характеризуемых большим количеством факторов, но могут быть выделены такие факторы, которые не могут быть измерены и выражены в каких-либо единицах, (ответственность поставщика, престиж фирмы, надежность партнера, предпочтения покупателя в выборе товара, мнение населения о методах работы органов местной власти и т.д.). В тоже время существует класс параметризируемых факторов, требует длительного времени и больших затрат на исследование системы (например, для объектов атомной энергетики). В таких случаях целесообразно прибегнуть к мнению экспертов – специалистов, чей опыт в исследуемой предметной области может существенно пополнить объем имеющихся сведений об объекте.

Методы учета не параметризируемых факторов при исследовании систем, либо параметризируемых, называют методами экспертных оценок. Эти методы позволяют объективно обрабатывать качественные данные, полученные в результате опроса специалистов, анкетирования, тестирования и прочими способами.

 

1. Ранжирование

 

Ранжирование представляет собой процедуру установления относительной значимости исследуемых объектов на основе их предпочтительности друг перед другом. При ранжировании каждому из объектов ставится в соответствие ранг. Ранг – это показатель, характеризующий порядковое место оцениваемого объекта или явления в группе других таких же объектов или явлений. Наиболее предпочтительному объекту обычно присваивается первый ранг, а наименее предпочтительному – последний. Предпочтение одного объекта перед другим может быть различным признакам. Так одно предприятие по сравнению с другим может выпускать более качественную продукцию (например, электронные платы), но уступать по шкале "консервативность – прогрессивность" технологии. Поэтому, ранжируя объекты, обычно оговаривают признак, по которому эти объекты сравниваются. В свете этого под ранжированием понимается расположение n объектов в порядке убывания или возрастания какого-либо признака Х. Признак Х, как правило, качественный, характеризует некоторое свойство, присущее всем сравниваемым объектам. Пусть n объектов проранжированы по некоторому признаку Х:

 

Табл.1

Номер объекта	1	2	3	…	n
Ранг объекта	Х1	Х2	Х3	…	Хn

 

Ранг Хі указывает то место, которое занимает і-й объект среди всех n объектов, ранжированных в соответствии с признаком Х. Величина ранга Хі является числом натурального ряда: 1, 2, 3, 4 и т.д.

Точность и надежность ранжирования зависят от количества объектов – чем их меньше, тем выше различимость и тем надежнее можно установить ранг.

Ранжирование n объектов m экспериментов по одному признаку Х приводит к появлению следующей таблице:

 

Табл.2

Номер объекта   Номер эксперта	1	2	3	…	n
1	Х11	Х12	Х13	…	Х1n
2	Х21	Х22	Х23	…	Х2n
3	Х31	Х32	Х33	…	Х3n
…				…
m	Хm1	Хm2	Хm3	…	Хmn

 

Естественно, что мнение специалистов далеко не всегда полностью совпадают. Поэтому для окончательного определения места, занимаемого объектом в сравнении с другими объектами, подсчитывается сумма рангов для каждого объекта. Объекту, получившему минимальную сумму, присваивается первый ранг, объекту с максимальной суммой – последней ранг. Остальные объекты получает промежуточные ранги.

Следует отметить, что итоговый ранг определяет лишь место, занимаемое каждым объектом среди других объектов. Для большего числа исследований этого достаточно, но иногда важно определить, – как далеко отстают друг от друга исследуемые объекты. В этих случаях метод ранжирования применяется в сочетании с методом непосредственной оценки. Для этого разрабатывается шкала интервалов – мера оценки качественного признака. Каждой градации шкалы интервалов присваивается определенный балл. Затем на шкале выделяются равные интервалы. Задачей экспертов является помещение всех исследуемых объектов в определенный оценочный интервал. Вследствие этого каждый из объектов получает определенный балл. По сумме баллов объекты получают места в итоговой ранжировке, а количественной мерой опережения или отставания объектов по исследуемому признаку будет служить разница в соответствующих баллах.

2. Конкордация

 

После того как в соответствии с некоторым признаком расставлены по местам важное место занимает вопрос о надежности полученных оценок. Мерой надежности полученных ранговых оценок является степень согласия экспертов или, другими словами, степень согласованности оценок, проставленных каждым из экспертов. Такая степень согласованности характеризуется коэффициентом конкордации (согласия):

 

W =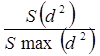

 

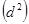Где S  - сумма квадратов отклонений суммарных рангов, выставленных каждому объекту всеми экспертами от среднего ранга:

 

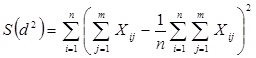
или

 

 

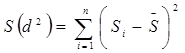
где

 

 

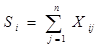
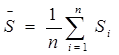
Величина 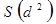 характеризует максимально возможное значение 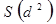. Очевидно, что чем выше согласие между экспертами, тем больший будет разброс выставленных сумм каждому объекту рангов относительно их среднего значения и тем выше значение 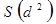. При полном совпадении мнений экспертов, когда все они дадут одинаковые оценки по каждому объекту, значение  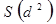примет значение 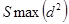, а коэффициент конкордации примет значение, равное единице. В свою очередь при отсутствии какого-то бы ни было согласия между экспертами, все суммарные ранги будут симметрично распределены вокруг своего среднего значения, вследствие чего величина  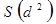и конкордации равны нулю.

Для определения значения 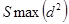 будем считать, что все эксперты присвоили одинаковые ранги всем объектам от значения 1 до значения n в виде чисел натурального ряда. Тогда значения Si образуют ряд:

 

m , 2m, 3m, ….. nm

 

в порядке, не обязательно соответствующих нумерации объектов. При этом среднее значение 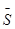 будет равно:

 

 

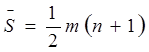
Вычитая из каждого элемента приведенного ряда значение, 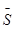 получим следующий ряд значений :

 

 

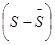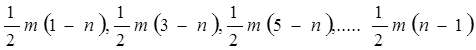
Далее найти сумму квадратов этого ряда:

 

 

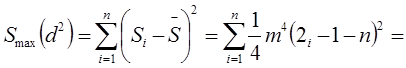
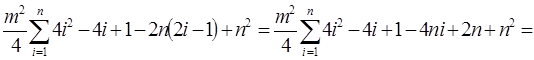
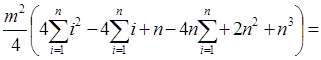
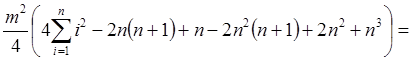
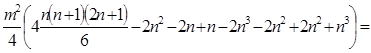
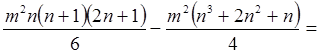
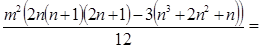
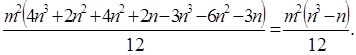
В соответствии с полученным результатом коэффициент конкордации можно записать в следующем виде:

 

 

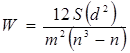
Собирательно свойства коэффициента конкордации выразятся так:

1.Коэффициент конкордации (согласия) принимает значение на числовом интервале от 0 до 1:

 

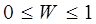
2.Равенство коэффициента конкордации нулю означает отсутствие связи между ранжировками исследователей и как следствие – отсутствие согласия. Близость W к нулю означает слабую степень согласия.

3.Равенство коэффициента конкордации единице означает, что все исследователи одинаково ранжируют объекты по данному признаку. Близость W к единице означает слабую степень согласия.

 

3.Ранжирование с совпавшими рангами

 

Иногда при ранжировании объектов отдельные эксперты не могут разделить предпочтения среди двух или большего количества объектов. При этом они ставят таким объектам одинаковые ранги. Такой вид ранжирования называется ранжированием с совпавшими рангами. Особенностью такого ранжирования является меняющийся диапазон изменения рангов, проставляемых каждым студентом Это в свою очередь влечет к неравновесности мнений студентов

 

Табл.3

№ предприятия	1	2	3	4	5	6
№ эксперта
1	2	2	1	3	3	3
2	1	4	2	3	5	6
3	2	3	3	1	4	4
4	2	1	1	2	3	3
5	2	4	1	4	3	4

 

Так по приведенной таблице видно, что мнение первого эксперта оценивается рангами от Х1 до Х3 ,а мнение второго – от Х1 доХ6.Обычный анализ привел бы к тому. Что мнение второго эксперта оказалось бы "тяжелее", мнения первого эксперта без имеющихся к тому оснований .

Чтобы устранить такую неравновесность мнений при ранжировании с совпавшими рангами применяют принцип нормирования ранжировок. Ранжировка считается нормированной, если сумма рангов в ней одинакова для каждого эксперта и равна сумме, которая была бы получена при отсутствии повторения рангов, то есть

 

,

 

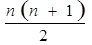где n- количество ранжируемых объектов.

Для того, чтобы ранжировку привести к нормальной необходимо привести ее в вид, в котором. Объекта, имеющим одинаковые ранги, приписывается ранг, равный среднему значению мест, которые эти объекты поделили между собой.

Процедура нормирования производит выравнивание ранжировок и приближение к объективности в размещении объектов. Легко убедится, что размещения объектов до и после нормирования отличаются друг от друга.

Расчет коэффициента в случае с совпавшими рангами осуществляется по следующей формуле:

 

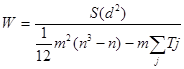, где

,

 

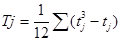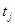
- количество повторений каждого ранга j – м студентом.

 

Практическая работа

 

Здесь осуществляется практическая реализация метода экспертных оценок в анализе качества обучающего процесса в ИП "Стратегия".

Этот раздел содержит расчеты показателей, сравнения результирующих данных, факторы, влияющие на показатели. Для получения всех этих данных был проведен опрос (анкетирование) среди студентов первого курса ИП "Стратегия" группы М-05-51.

Оценивание по десятибалльной системе способность студентов понимать изучаемые дисциплины

 

Табл.4

Дисциплина	Английский язык	Макроэкономика	Право	Украинский язык	Высшая математика
№ студентов
1	8	10	6	9	10
2	8	10	8	9	6
3	8	8	9	8	6
4	10	8	8	9	3
5	10	8	8	6	1
6	10	10	10	10	9
7	9	10	9	10	8
8	7	7	9	10	10
9	7	5	6	9	5
10	8	4	7	9	3
11	10	10	8	7	5
12	8	10	10	10	8
13	9	8	8	10	5
14	8	6	8	9	2
15	8	7	8	9	7
16	10	9	9	7	1
17	10	10	10	10	10
18	10	7	10	10	10
19	10	9	9	10	8
20	10	8	9	8	5

 

Табл.5 Ранжирование с совпавшими рангами

Дисциплина	Английский язык	Макроэкономика	Право	Украинский язык	Высшая математика
№ студентов
1	4	1,5	5	3	1,5
2	3,5	1	3,5	2	5
3	4,5	4,5	1	45	5
4	1	3,5	3,5	2	5
5	1	1,5	1,5	4	5
6	2,5	2,5	2,5	25	5
7	3,5	1,5	3,5	15	5
8	4,5	4,5	3	15	1,5
9	2	4,5	3	1	4,5
10	2	4	3	1	5
11	1,5	1,5	3	4	5
12	4,5	2	2	2	4,5
13	2	3,5	3,5	1	5
14	2,5	4	2,5	1	5
15	2,5	4,5	2,5	1	4,5
16	1	2,5	2,5	4	5
17	3	3	3	3	3
18	2,5	5	2,5	25	2,5
19	1,5	3,5	3,5	15	5
20	1	3,5	2	35	5
Сумма рангов	50,5	62	56,5	46,5	87

 

Производим расчет коэффициента конкордации в случае с совпавшими рангами по данным таблицы.

 

n=5 m=20, 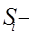 сумма рангов.

 

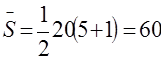
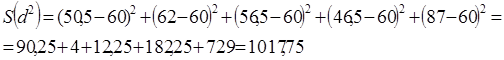
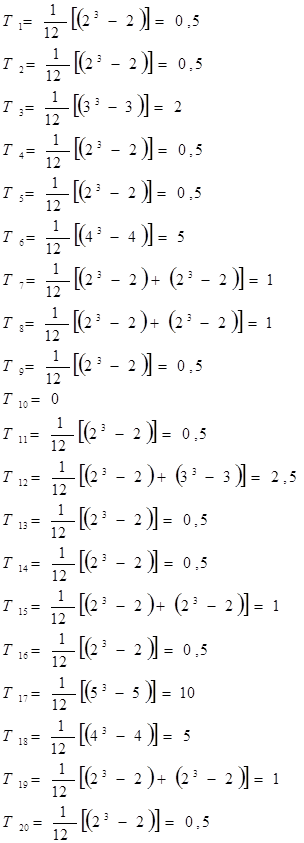
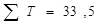
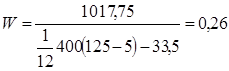
-близкое к нулю значение W свидетельствует об отсутствии согласия во мнениях студентов.

Оценивание по десяти балльной системе способность преподавателей излагать материал ясно и доступно

 

Табл.6

Дисциплина	Английский язык	Макроэкономика	Право	Украинский язык	Высшая математика
№ студента
1	9	10	8	9	10
2	10	10	8	10	10
3	10	10	10	10	10
4	10	9	9	8	5
5	9	9	9	10	8
6	9	8	10	9	8
7	8	10	8	10	9
8	10	7	6	9	7
9	10	8	8	10	10
10	10	7	7	10	9
11	9	8	7	8	5
12	10	10	8	7	5
13	8	10	7	10	10
14	10	8	6	10	10
15	10	7	1	8	2
16	9	9	10	10	9
17	9	9	4	8	2
18	10	10	8	10	10
19	10	5	7	10	10
20	10	10	6	10	10

 

Табл.7 Ранжирование с совпавшими рангами

Дисциплина	Английский язык	Макроэкономика	Право	Украинский язык	Высшая математика
№ студента
1	2,5	1,5	5	2,5	1,5
2	2,5	2,5	5	2,5	2,5
3	3	3	3	3	3
4	1	2,5	2,5	4	5
5	3	3	3	1	5
6	2,5	4,5	1	2,5	4,5
7	4,5	1,5	4,5	1,5	3
8	1	3,5	5	2	3,5
9	2	4,5	4,5	2	2
10	1,5	4,5	4,5	1,5	3
11	1	2,5	4	2,5	5
12	1,5	1,5	3	4	5
13	4	2	5	2	2
14	2	4	5	2	2
15	1	3	5	2	4
16	4	4	1,5	1,5	4
17	1,5	1,5	4	3	5
18	2,5	2,5	5	2,5	2,5
19	2	5	4	2	2
20	2,5	2,5	5	2,5	2,5
Сумма	45,5	59,5	79,5	46,5	67

 

Производим расчет коэффициента конкордации по данным таблицы

 

N=5, m=20, 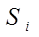- сумма рангов

 

 

 

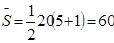
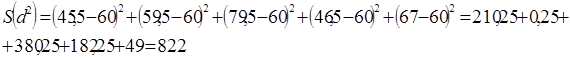
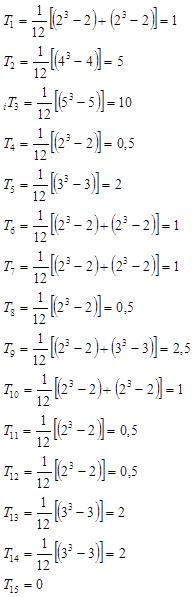
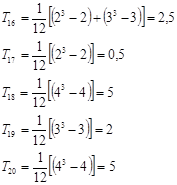
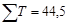
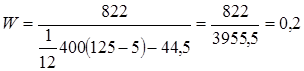
-близкое к единице значение W свидетельствует об отсутствии согласия между студентами.

 

Вывод

 

При написании курсовой работы на тему "Метод экспертных оценок в анализе качества обучающего процесса в ИП "Стратегия" были достигнуты систематизация, закрепление и расширение теоретических и практических знаний по дисциплине "Теория вероятности и математическая статистика", а также способность применять эти знания на практике. При помощи данного метода было определено качество обучающего процесса и качество изложения преподавателями материала студентам, а также способность студентами понимать изучаемый материал. Для проведения этого анализа было проведено анкетирование среди студентов первого курса по пяти изучаемых ими дисциплинам, где каждый из 20 опрашиваемых студентов должен был оценить по десятибалльной системе каждую из характеристик, изучаемых ими в семестре дисциплин. В результате опроса был получен результат, который говорит об отсутствии между студентами согласия в понимании ими изучаемых дисциплин и в способности преподавателями излагать материал ясно и доступно.

 

Список литературы

 

Гмурман В.Е., Теория вероятности и математическая статистика. Учебное пособие для вузов. – 8-е издание, 2002г.

---

Дата добавления: 2019-07-15; просмотров: 269; Мы поможем в написании вашей работы!

Поделиться с друзьями:

---

---

Мы поможем в написании ваших работ!