Расчёт быстроходной ступени редуктора
Факультет КМК
Кафедра К3-КФ
Проектирование привода цепного транспортера.
Студент _______________ (Бедняшов Р.В.)
Группа МСХ-62
Консультант _______________ (Комаров И.А.)
Г. Калуга 2005
Содержание
2. Кинематическая схема привода ленточного конвейера 4
3. Выбор электродвигателя 5
4. Определение мощности, крутящего момента и частоты вращения каждого вала привода 7
5. Проектный и проверочный расчёт зубчатых передач 9
6. Определение диаметров валов 20
7. Выбор и проверка подшипников качения по динамической грузоподъёмности. 21
8. Проверочный расчёт наиболее нагруженного вала на усталостную прочность и жёсткость 23
9. Выбор и расчёт шпоночных соединений 26
10. Литература 28
2. Кинематическая схема привода ленточного конвейера

Выбор электродвигателя
1. Общий коэффициент полезного действия:
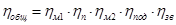
 - КПД упругой и компенсирующей муфты
- КПД упругой и компенсирующей муфты
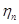 - КПД передачи
- КПД передачи
 -КПД звёздочки
-КПД звёздочки
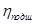 - КПД подшипника
- КПД подшипника

2. Мощность электродвигателя:
 кВт
кВт
где Ft = 5300 Н – окружное усилие на барабане;
v = 0,68 м/с – скорость цепей транспортёра;
По таблице определяем, что Рэл = 7,5 кВт.
3. Частота вращения приводного вала:
 мин-1,
мин-1,
где n4 – частота вращения приводного вала [мин-1];
 мм – диаметр звёздочки;
мм – диаметр звёздочки;
4. Частота вращения э/д:
 мин-1
мин-1
где n΄эд – предварительная частота вращения э/д [мин-1];
Uобщ – общее передаточное число;
 , где
, где
 ;
;
Uт =4
Принимаем nэд = 730 мин-1.
Выбираем тип э/д 4А160S8/730, который имеет следующие параметры: Рэд = 7,5 кВт, nэд = 730 мин-1.
Определение мощности, крутящего момента и частоты вращения каждого вала привода
Определим мощности:  кВт;
кВт;
 ;
;
 ;
;
 ;
;
где  – мощность на валах редуктора, быстроходного, промежуточного, тихоходного валов и приводного вала,
– мощность на валах редуктора, быстроходного, промежуточного, тихоходного валов и приводного вала,  – коэффициенты полезного действия быстроходной и тихоходной ступени, муфты и звёздочки соответственно.
– коэффициенты полезного действия быстроходной и тихоходной ступени, муфты и звёздочки соответственно.
Определим частоту вращения:  ;
;
 ;
;
 ;
;
 ;
;
где  – частота вращения на валах редуктора, быстроходного, промежуточного, тихоходного валов и приводном вале,
– частота вращения на валах редуктора, быстроходного, промежуточного, тихоходного валов и приводном вале, 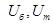 – передаточное число, быстроходной и тихоходной ступеней редуктора соответственно.
– передаточное число, быстроходной и тихоходной ступеней редуктора соответственно.
Определим крутящие моменты:  ;
;
 ;
;
 ;
;
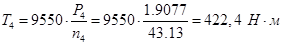
где  – крутящие моменты на валах редуктора быстроходного, промежуточного, тихоходного и приводного валов .
– крутящие моменты на валах редуктора быстроходного, промежуточного, тихоходного и приводного валов .
Результаты расчётов занесём в таблицу 1.
Таблица 1.
| Вал | Мощность 
| Частота вращения 
| Крутящий момент 
|
| 1 | 2,18 | 750 | 27,7 |
| 2 | 2,09 | 172,5 | 115,76 |
| 3 | 2,01 | 43,13 | 444.5 |
| 4 | 1.91 | 43,13 | 422,4 |
Проектный и проверочный расчёт зубчатых передач
Расчёт тихоходной ступени редуктора.
Материал колеса и шестерни – сталь 45 улучшение. Таким образом, учитывая, что термообработка зубчатых колёс – улучшение, по таблице 3.1 имеем:
для шестерни: 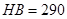 ,
,  ,
,  ;
;
для колеса:  ,
, 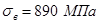 ,
,  ;
;
где 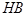 – твёрдость рабочей поверхности зубьев,
– твёрдость рабочей поверхности зубьев,  и
и 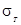 – предел прочности материала на растяжение и предел текучести материала.
– предел прочности материала на растяжение и предел текучести материала.
Определим коэффициенты приведения на контактную выносливость  и на изгибную выносливость
и на изгибную выносливость  по таблице 4.1 лит. 1, учитывая режим работы №0:
по таблице 4.1 лит. 1, учитывая режим работы №0:  ;
;  .
.
Определим число циклов перемены напряжений. Числа циклов  перемены напряжений соответствуют длительному пределу выносливости. По графику 4.3 определяем числа циклов на контактную и изгибную выносливость соответственно:
перемены напряжений соответствуют длительному пределу выносливости. По графику 4.3 определяем числа циклов на контактную и изгибную выносливость соответственно:  ,
,  ,
,  .
.
Определим суммарное число циклов перемены напряжений для шестерни и колеса соответственно: 
 , где
, где  и
и 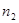 – частота вращения шестерни и колеса соответственно;
– частота вращения шестерни и колеса соответственно;  – число вхождений в зацепление зубьев шестерни или колеса соответственно за один его оборот.
– число вхождений в зацепление зубьев шестерни или колеса соответственно за один его оборот.
Так как  , то принимаем
, то принимаем  .
.
Так как  , то принимаем
, то принимаем  .
.
Найдём эквивалентное число циклов перемены напряжений для расчёта на изгибную выносливость:  ,
, 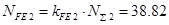 , где
, где  – коэффициенты приведения на изгибную выносливость;
– коэффициенты приведения на изгибную выносливость;  – суммарное число циклов перемены напряжений для шестерни или колеса.
– суммарное число циклов перемены напряжений для шестерни или колеса.
Так как  , то принимаем
, то принимаем  .
.
Так как  , то принимаем
, то принимаем  .
.
Определим допускаемые напряжения для расчётов на выносливость. По таблице 4.3 находим, что  ,
, 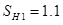 ,
,  ,
,  – для шестерни и
– для шестерни и 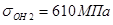 ,
, 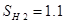 ,
, 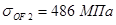 ,
, 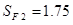 – для зубчатого колеса,
– для зубчатого колеса,
где  и
и  – длительный предел контактной выносливости и коэффициент безопасности;
– длительный предел контактной выносливости и коэффициент безопасности;  и
и  – длительный предел изгибной выносливости и коэффициент безопасности; Найдём предельные допускаемые контактные и изгибные напряжения:
– длительный предел изгибной выносливости и коэффициент безопасности; Найдём предельные допускаемые контактные и изгибные напряжения: 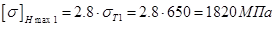 ,
,  ,
,  ,
, 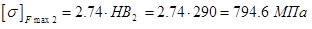 , где
, где  – предел текучести материала колеса или шестерни;
– предел текучести материала колеса или шестерни;
Определим допускаемые контактные напряжения и напряжения изгиба при неограниченном ресурсе передачи:  ,
,  ,
, 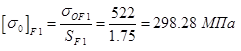 ,
,  , где
, где  и
и  – длительный предел контактной выносливости и коэффициент безопасности;
– длительный предел контактной выносливости и коэффициент безопасности;  и
и  – длительный предел изгибной выносливости и коэффициент безопасности.
– длительный предел изгибной выносливости и коэффициент безопасности.
Проверим передачу на контактную выносливость и изгибную выносливость:  ,
,  ,
,  ,
,  .
.
Выбираем допускаемое контактное напряжение как меньшее из значений:  .
.

Принимаем 
Определим предварительное значение межосевого расстояния:

где ψа = 0,4 – коэффициент ширины тихоходной ступени.
 =4– передаточное число ступени редуктора;
=4– передаточное число ступени редуктора;
 = 210.3 МПа – допускаемое контактное напряжение;
= 210.3 МПа – допускаемое контактное напряжение;
 =1.04 – коэффициент, учитывающий распределение нагрузки между зубьями, определяем по рис. 6.2;
=1.04 – коэффициент, учитывающий распределение нагрузки между зубьями, определяем по рис. 6.2;
 =422.4Н м– крутящий момент на валу колеса;
=422.4Н м– крутящий момент на валу колеса;
 – коэффициент нагрузки на контактную выносливость, определяется следующим образом.
– коэффициент нагрузки на контактную выносливость, определяется следующим образом.
Найдём коэффициенты нагрузки на контактную и изгибную выносливость по формулам:
 и
и  ,
,
где  и
и  – коэффициенты концентрации нагрузки по ширине зубчатого венца;
– коэффициенты концентрации нагрузки по ширине зубчатого венца;
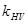 и
и 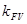 – коэффициенты динамической нагрузки (учитывают внутреннюю динамику передачи).
– коэффициенты динамической нагрузки (учитывают внутреннюю динамику передачи).
 - для прирабатывающихся зубьев при постоянной нагрузке;
- для прирабатывающихся зубьев при постоянной нагрузке;
Коэффициент  определяется по табл. 5.4 в зависимости от вида передачи (в данном случае цилиндрическая косозубая). Находим, что
определяется по табл. 5.4 в зависимости от вида передачи (в данном случае цилиндрическая косозубая). Находим, что  и
и  . Теперь находим значения коэффициентов нагрузки
. Теперь находим значения коэффициентов нагрузки
 и
и  .
.
Принимаем а = 250 мм
Определяем рабочую ширину колеса:
 .
.
Ширина шестерни:  .
.
Вычислим модуль передачи по формуле:
 ,где
,где  =215.7МПа–изгибное напряжение на колесе;
=215.7МПа–изгибное напряжение на колесе;  ,
,  . Тогда
. Тогда 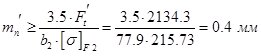 . Из стандартного ряда значений
. Из стандартного ряда значений  по ГОСТ 9563–60 выбираем значение
по ГОСТ 9563–60 выбираем значение  .
.
Определим минимально возможный угол наклона зуба  .
.
Рассчитываем предварительное суммарное число зубьев: 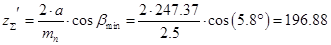 . Округляем это число и получаем
. Округляем это число и получаем  .
.
Определяем действительное значение угла  и сравниваем его с минимальным значением:
и сравниваем его с минимальным значением:
 .
.
Найдём число зубьев шестерни  и колеса
и колеса  , учитывая что минимальное число зубьев для косозубой цилиндрической передачи
, учитывая что минимальное число зубьев для косозубой цилиндрической передачи  ;
;  .
.
Найдём фактическое передаточное число передачи:  . Таким образом отклонение фактического передаточного числа данной ступени редуктора от номинального значения
. Таким образом отклонение фактического передаточного числа данной ступени редуктора от номинального значения  .
.
Проверим зубья колёс на изгибную выносливость. Для колеса получим: 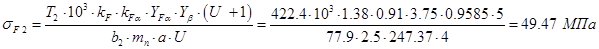 где
где  – коэффициент нагрузки при расчёте на изгибную выносливость;
– коэффициент нагрузки при расчёте на изгибную выносливость;
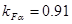 – коэффициент, учитывающий распределение нагрузки между зубьями, выбираем по табл. 6.4;
– коэффициент, учитывающий распределение нагрузки между зубьями, выбираем по табл. 6.4;
 – коэффициент, учитывающий форму зуба, находится по табл. 6.2 лит. 1;
– коэффициент, учитывающий форму зуба, находится по табл. 6.2 лит. 1;
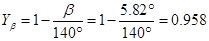 – коэффициент, учитывающий наклон зуба.
– коэффициент, учитывающий наклон зуба.
Сравниваем полученное значение напряжения с допускаемым напряжением при расчёте на изгиб зубьев колеса:  .
.
Для шестерни:  ,
,
где 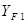 и
и  – коэффициенты, учитывающие форму зуба, определяются по табл. 6.2.
– коэффициенты, учитывающие форму зуба, определяются по табл. 6.2.
Сравним полученное значение напряжения с допускаемым напряжением при расчёте на изгиб зубьев шестерни:  .
.
Определим диаметры делительных окружностей шестерни и колеса соответственно.
 ,
,  ,
,
где  – модуль зубчатых колёс;
– модуль зубчатых колёс;
 – угол наклона зуба;
– угол наклона зуба;
Вычислим диаметры окружностей вершин зубьев  и впадин зубьев
и впадин зубьев  .
.
 ;
;  ;
;  ;
;  .
.
Расчёт быстроходной ступени редуктора
Материал колеса и шестерни – сталь 45. Таким образом, учитывая, что термообработка зубчатых колёс и шестерни – улучшение, имеем:
для шестерни:,  ;
;
для колеса:,  ;
;
где  – твёрдость рабочей поверхности зубьев,
– твёрдость рабочей поверхности зубьев,  – предел текучести материала.
– предел текучести материала.
Определим твёрдость зубьев шестерни и колеса:
 ;
;
 .
.
Определимкоэффициенты приведения на контактную выносливость  и на изгибную выносливость
и на изгибную выносливость  по таблице 4.1., учитывая режим работы №3:
по таблице 4.1., учитывая режим работы №3:  ;
;  .
.
Определим число циклов перемены напряжений.
Определим суммарное число циклов перемены напряжений для шестерни и колеса соответственно:
 ,
,  ,
,
где  –ресурс передачи;
–ресурс передачи; 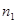 и
и  – частота вращения шестерни и колеса соответственно;
– частота вращения шестерни и колеса соответственно;  =
=  =1 – число вхождений в зацепление зубьев шестерни или колеса соответственно за один его оборот.
=1 – число вхождений в зацепление зубьев шестерни или колеса соответственно за один его оборот.
Числа циклов  перемены напряжений соответствуют длительному пределу выносливости. По графику 4.3. определяем числа циклов на контактную и изгибную выносливость соответственно:
перемены напряжений соответствуют длительному пределу выносливости. По графику 4.3. определяем числа циклов на контактную и изгибную выносливость соответственно:
 ,
,  ,
,  .
.
Определим эквивалентное число циклов перемены напряжений для расчёта на контактную выносливость:

 ,
,
где  – коэффициенты приведения на контактную выносливость;
– коэффициенты приведения на контактную выносливость;  – суммарное число циклов перемены напряжений для шестерни или колеса.
– суммарное число циклов перемены напряжений для шестерни или колеса.
Так как 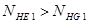 , то принимаем
, то принимаем  и
и  , то
, то
 .
.
Определим эквивалентное число циклов перемены напряжений для расчёта на изгибную выносливость:
 ,
,
 ,
,
где  – коэффициенты приведения на изгибную выносливость;
– коэффициенты приведения на изгибную выносливость;  – суммарное число циклов перемены напряжений для шестерни или колеса.
– суммарное число циклов перемены напряжений для шестерни или колеса.
Так как 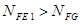 и
и  , то принимаем
, то принимаем 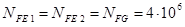 .
.
Определим допускаемые напряжения для расчётов на выносливость. По таблице 4.3 находим
для шестерни:
 ,
,

 ,
, 
для зубчатого колеса:
 ,
,  ,
,
 ,
,  ,
,
где  и
и  – длительный предел контактной выносливости и коэффициент безопасности;
– длительный предел контактной выносливости и коэффициент безопасности;  и
и  – длительный предел изгибной выносливости и коэффициент безопасности;
– длительный предел изгибной выносливости и коэффициент безопасности;  – твёрдость зубьев шестерни или колеса.
– твёрдость зубьев шестерни или колеса.
Определим предельные допускаемые контактные и изгибные напряжения:
 ,
,

 ,
,

где  – предел текучести материала колеса или шестерни;
– предел текучести материала колеса или шестерни; 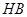 –твёрдость зубьев шестерни или колеса.
–твёрдость зубьев шестерни или колеса.
Проверим передачу на контактную выносливость:
 ,
,  ,
,  ,
,  .
.
Принимаем допускаемое контактное напряжение как меньшее значение:


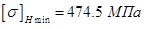 .
.
Определим коэффициенты нагрузки на контактную и изгибную выносливость по формулам:
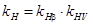 и
и  ,
,
где  и
и  – коэффициенты концентрации нагрузки по ширине зубчатого венца;
– коэффициенты концентрации нагрузки по ширине зубчатого венца; 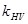 и
и  – коэффициенты динамической нагрузки (учитывают внутреннюю динамику передачи).
– коэффициенты динамической нагрузки (учитывают внутреннюю динамику передачи).
Относительная ширина зубчатого венца находится по формуле
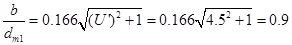 ,
,
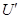 =4.5 – передаточное число данной ступени редуктора.
=4.5 – передаточное число данной ступени редуктора.
По таблице 5.2. и 5.3, схемы 2 расположения зубчатых колёс относительно опор и варианта соотношения термических обработок “a” находим  ,
, 
Тогда


Значения 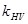 определяются по табл. 5.6
определяются по табл. 5.6
Коэффициент  определяется по табл. 5.4 в зависимости от вида передачи.
определяется по табл. 5.4 в зависимости от вида передачи.
Принимаем 8-ю степень точности изготовления передачи находим, что
 и
и  .
.
Теперь находим значения коэффициентов нагрузки
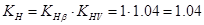
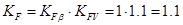
Определим коэффициент ширины быстроходной ступени 

Определяем рабочую ширину колеса:
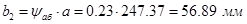 .
.
Ширина шестерни:  .
.
Вычислим модуль передачи по формуле:
 ,
,
где  =257.1 МПа – изгибное напряжение на колесе;
=257.1 МПа – изгибное напряжение на колесе;  ,
,  . Тогда
. Тогда  . Из стандартного ряда значений
. Из стандартного ряда значений  по ГОСТ 9563–60 выбираем значение
по ГОСТ 9563–60 выбираем значение  .
.
Определим минимально возможный угол наклона зуба  .
.
Рассчитываем предварительное суммарное число зубьев:  . Округляем это число и получаем
. Округляем это число и получаем  .
.
Определяем действительное значение угла  и сравниваем его с минимальным значением:
и сравниваем его с минимальным значением:
 .
.
Найдём число зубьев шестерни  и колеса
и колеса  , учитывая, что минимальное число зубьев для косозубой цилиндрической передачи
, учитывая, что минимальное число зубьев для косозубой цилиндрической передачи  ;
;  .
.
Найдём фактическое передаточное число передачи:  . Таким, образом отклонение фактического передаточного числа данной ступени редуктора от номинального значения
. Таким, образом отклонение фактического передаточного числа данной ступени редуктора от номинального значения 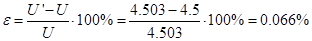 .
.
Проверим зубья колёс на изгибную выносливость. Для колеса получим:  где
где  – коэффициент нагрузки при расчёте на изгибную выносливость;
– коэффициент нагрузки при расчёте на изгибную выносливость;
 – коэффициент, учитывающий распределение нагрузки между зубьями, выбираем по табл. 6.4;
– коэффициент, учитывающий распределение нагрузки между зубьями, выбираем по табл. 6.4;
 – коэффициент, учитывающий форму зуба, находится по табл. 6.2 лит. 1;
– коэффициент, учитывающий форму зуба, находится по табл. 6.2 лит. 1;
 – коэффициент, учитывающий наклон зуба.
– коэффициент, учитывающий наклон зуба.
Сравниваем полученное значение напряжения с допускаемым напряжением при расчёте на изгиб зубьев колеса:  .
.
Определим диаметры делительных окружностей шестерни и колеса соответственно.
 ,
,  ,
,
где  – модуль зубчатых колёс;
– модуль зубчатых колёс;
 – угол наклона зуба;
– угол наклона зуба;
Проверка
Вычислим диаметры окружностей вершин зубьев  и впадин зубьев
и впадин зубьев 
 ;
;  ;
;  ;
;  .
.
Определим силы, действующие на валы зубчатых колёс.
Окружную силу на среднем находим по формуле:
 Н,
Н,
Осевая сила на шестерне:
 Н,
Н,
Радиальная сила на шестерне:
 Н
Н
Определение диаметров валов
Определим диаметр быстроходного вала шестерни:  , где
, где  – момент на быстроходном валу. Примем
– момент на быстроходном валу. Примем  . Сравним этот диаметр с диаметром вала электродвигателя, при этом должно выполняться условие
. Сравним этот диаметр с диаметром вала электродвигателя, при этом должно выполняться условие  – условие выполняется.
– условие выполняется.
Определим диаметр посадочной поверхности подшипника:  . Примем dк = 30мм. Диаметр вала под колесо
. Примем dк = 30мм. Диаметр вала под колесо  . Рассчитаем диаметр буртика для упора подшипника:
. Рассчитаем диаметр буртика для упора подшипника:  . Примем d бк = 32мм.
. Примем d бк = 32мм.
Определим диаметры промежуточного вала:  , где Т2 – момент на промежуточном валу. Примем dк = 35 мм. Для найденного диаметра вала выбираем значения:
, где Т2 – момент на промежуточном валу. Примем dк = 35 мм. Для найденного диаметра вала выбираем значения:  – приблизительная высота буртика,
– приблизительная высота буртика,  – максимальный радиус фаски подшипника,
– максимальный радиус фаски подшипника,  – размер фасок вала. Диаметр вала под колесо
– размер фасок вала. Диаметр вала под колесо 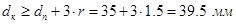 . Примем диаметр dк =38. Диаметр буртика для упора колеса
. Примем диаметр dк =38. Диаметр буртика для упора колеса  . Принимаем dбк = 42мм.
. Принимаем dбк = 42мм.
Определим диаметр тихоходного вала: 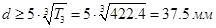 , где
, где  – момент на тихоходном валу. Примем
– момент на тихоходном валу. Примем  . Для найденного диаметра вала выбираем значения:
. Для найденного диаметра вала выбираем значения:  – приблизительная высота буртика,
– приблизительная высота буртика,  – максимальный радиус фаски подшипника,
– максимальный радиус фаски подшипника,  – размер фасок вала. Определим диаметр посадочной поверхности подшипника:
– размер фасок вала. Определим диаметр посадочной поверхности подшипника:  . Так как стандартные подшипники имеют посадочный диаметр, кратный
. Так как стандартные подшипники имеют посадочный диаметр, кратный  -ти, то принимаем
-ти, то принимаем  . Рассчитаем диаметр буртика для упора подшипника:
. Рассчитаем диаметр буртика для упора подшипника:  . Пусть
. Пусть  .
.
Дата добавления: 2019-07-15; просмотров: 406; Мы поможем в написании вашей работы! |

Мы поможем в написании ваших работ!
