Отыскание периодического решения в области резонанса.
Тогда l=mlо; w2 = 1+ aо m, (24) (aо , m - расстройка , реальный физический резонанс наступает при aо ¹ 0).
Тогда исследуемое уравнение имеет вид :
(25)
При m = 0 периодическое решение будет иметь вид :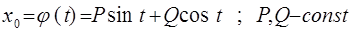 
(26)
Следуя Пуанкаре, мы можем предположить периодическое решение в виде:
(27);
Начальные условия возьмем как и раньше:
Аналогично тому, как мы это делали в предыдущих параграфах. Подставляем (27) в (25) и, сравнивая коэффициенты при b1 b2, m и других интересующих нас величинах, получим уравнение, которым удовлетворяет A, B, C, D, E, F. Начальные условия для этих уравнений определим, если подставим (28) в (27).
(29)
Запишем условия периодичности для (27):
Делим на m:
( 30a )
Необходимым условием существования периодического решения является:
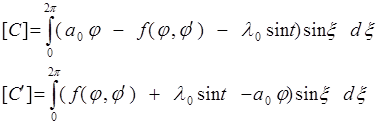
Эти уравнения определяют P и Q решения (26), в близости к которому устанавливается периодическое решение. Они могут быть записаны в раскрытой форме :
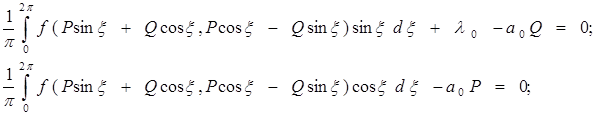
(31)
Для существования искомого периодического решения достаточно неравенство 0 детерминанта: (см. § 1).
D, Е и их производные найдутся из (29) при помощи формул аналогичных (15). Заметим, что (30) мы можем определить b1, b2, в виде рядов по степеням m. Таким образом, мы можем (27) как и в § 1 представить в виде ряда.
(33)
P,Q-определяются формулами (31) (32).
Исследование устойчивости периодических решений в области резонанса
|
|
|
Аналогично тому, как мы это делали в § 2, составим уравнение первого приближения, порожденное решением (33).
Решение опять будем искать в виде 
. Однако нет необходимости проделывать все выкладки заново. Воспользуемся результатами § 2, приняв:
Из формул (22) 
(34) , тогда 
D - тот же Якобиан, что и (32). Распишем его:
(36)
;
Тогда, зная функцию f, мы можем вычислить D в виде функции P, Q и aо.
Заметим, что равенство (23 а) в нашем случае имеет вид:
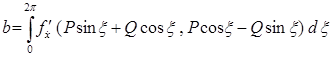; (37)
Опираясь на результаты исследования, полученных в § 2, нужно рассмотреть при исследовании устойчивости два случая: (при достаточно малых m)
1) p2 - q < 0 
2) p2 - q > 0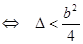 
В первом случае устойчивость характеризуется условием q < 1 или, что то же самое b < 0.
Во втором случае 
(*) последнее может быть выполнено только, если b < 0, а D > 0. Нетрудно видеть, что необходимым достаточным условием в обоих случаях является b < 0, D > 0. (Это можно получить из неравенства (*) ).
Применение общих формул, полученных в предыдущих параграфах, к теории захватывания в регенеративном приемнике для случая, когда характеристика - кубическая парабола.
Мы рассмотрим простой регенеративный приемник с колебательным контуром в цепи сетки, на который действует внешняя сила Ро sin w1 t.
|
|
|
Дифференциальное уравнение колебаний данного контура следующее:
(39)
Считая, что анодный ток зависит только от сеточного напряжения, а также, что характеристикой является кубическая парабола:
(40)
S-крутизна характеристики, К - напряжение насыщения 
.
Далее, вводя обозначения: 
Получим дифференциальное уравнение для х:
(41)
А: (случай далекий от резонанса).
Для него применяем результаты § 1, полагая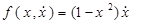 
.
Исходное решение в не посредственной близости, к которому устанавливается искомое решение следующее:
Если w > 1, т.е. wо > w1, то разность фаз равна 0, если w < 1, то разность фаз равна p. В этом отношении все происходит в первом приближении также, как и при обычном линейном резонансе. Устойчивость определяется знаком b (b < 0).
(42).
Т.е. те решения, для которых выполняется это условие, устойчивы.
В: (область резонанса , § 3, 4).
В качестве исходного периодического решения, в непосредственной близости к которому устанавливается искомое, будет решение следующего вида: x = P sin t + Q cos t (P, Q - const).
Запишем уравнение, определяющее эти P и Q, т.е. соотношение (31) для нашего случая.
|
|
|
Или преобразовав их, получим следующее:
Полагая Р = R sin j; Q = R cos j. Далее найдем для амплитуды R и фазы j для того исходного периодического решения, в близости к которому устанавливается рассматриваемое периодическое решение , соотношения связывающие их :
Первая формула дает "резонансную поверхность" для амплитуды. Вторая - для фазы. По (38) условия устойчивости имеют вид b < 0, D > 0. Считаем b и D через формулы (35-37).
(46)
Т.е. решение является устойчивым, если удовлетворяется условие (**). В заключение выпишем формулы для вычисления aо, соответствующего ширине захватывания для рассматриваемого случая.
1) 
a0 - является общим корнем уравнений
2) 
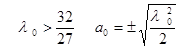
Сама ширина Dw, отсчитанная от одной границы захватывания до другой выражается следующим образом: Dw = aо w2о (MS - c r). Можно дать простые формулы для вычисления ширины захватывания в следующих случаях:
а) l2о << 1; Dw = wо Ро/Vоg.
б) для очень сильных сигналов 
( Vоg - амплитуда сеточного напряжения при отсутствии внешней силы).
Список литературы
1. Андронов А.А. Собрание трудов, издательство "Академии наук СССР", 1956.
|
|
|
2. Андронов А.А., Витт А. К теории захватывания Ван дер Поля. . Собрание трудов, издательство "Академии наук СССР", 1956.
3. Ляпунов А. Общая задача об устойчивости движения, Харьков, 1892.
Дата добавления: 2019-07-15; просмотров: 122; Мы поможем в написании вашей работы! |
Мы поможем в написании ваших работ!