МНОГОМАСШТАБНЫЙ АНАЛИЗ И ВЕЙВЛЕТЫ
Факультет прикладной математики и информатики
Кафедра математической физики
ГРОМОВА МАРИЯ МИХАЙЛОВНА
ОПРЕАТОРЫ В ВЕЙВЛЕТНОМ БАЗИСЕ
Курсовая работа студентки 4 курса
Научный руководитель:
Глушцов Анатолий Ильич
Кафедры МФ
Кандидат физ.-мат. наук
Минск 2004
СОДЕРЖАНИЕ
ВВЕДЕНИЕ………..………………………………………………………..3
1. МНОГОМАСШТАБНЫЙ АНАЛИЗ И ВЕЙВЛЕТЫ………………...5
2. БЫСТРОЕ ВЕЙВЛЕТ-ПРЕОБРАЗОВАНИЕ….……………………...9
3. ДВУМЕРНЫЕ ВЕЙВЛЕТЫ…………………………………………..12
4. МАТРИЧНЫЕ ОПЕРАЦИИ………………………………………….13
4.1. Матричное умножение………………………………………...13
4.2. Обращение матрицы…………………………………………...16
4.3. Вычисление экспоненты, синуса и косинуса от матрицы.….16
ЛИТЕРАТУРА……………………………………………………………18
ВВЕДЕНИЕ
Вейвлет-преобразование сигналов (wavelet transform), теория которого оформилась в начале 90-х годов, является не менее общим по областям своих применений, чем классическое преобразование Фурье. Принцип ортогонального разложения по компактным волнам состоит в возможности независимого анализа функции на разных масштабах ее изменения. Вейвлет-представление сигналов (функций времени) является промежуточным между полностью спектральным и полностью временным представлениями.
Компактные волны относительно независимо были предложены в квантовой физике, физике электромагнитных явлений, математике, электронике и сейсмогеологии. Междисциплинарные исследования привели к новым приложениям данных методов, в частности, в сжатии образов для архивов и телекоммуникаций, в исследованиях турбулентности, в физиологии зрительной системы, в анализе радарных сигналов и предсказании землетрясений. К сожалению, объем русскоязычной научной литературы по тематике вейвлет-преобразований (да и нейронных сетей) относительно невелик.
|
|
|
Базовая идея восходит к временам 200-летней давности и принадлежит Фурье: аппроксимировать сложную функцию взвешенной суммой простых функций, каждая из которых, в свою очередь, получается из одной функции-прототипа. Эта функция-прототип выполняет роль строительного блока, а искомая аппроксимация получается комбинированием одинаковых по структуре блоков. При этом, если "хорошая" аппроксимация получается при использовании небольшого числа блоков, то тем самым достигается значительное уплотнение информации. В качестве таких блоков Фурье использовал синусоиды с различными периодами.
Что прежде всего отличает вейвлет-анализ от анализа Фурье? Основным недостатком Фурье-преобразования является его "глобальная" чувствительность к "локальным" скачкам и пикам функции. При этом модификация коэффициентов Фурье (например, обрезание высоких гармоник с целью фильтрации шума) вносит одинаковые изменения в поведение сигнала на всей области определения. Это особенность оказывается полезной для стационарных сигналов, свойства которых в целом мало меняются со временем.
|
|
|
При исследовании же нестационарных сигналов требуется использование некоторых локализованных во времени компактных волн, коэффициенты разложения по которым сохраняют информацию о дрейфе параметров аппроксимируемой функции. Первые попытки построения таких систем функций сводились к сегментированию сигнала на фрагменты ("окна") с применением разложения Фурье для этих фрагментов. Соответствующее преобразование - оконное преобразование Фурье - было предложено в 1946-47 годах Jean Ville и, независимо, Dennis Gabor. В 1950-70-х годах разными авторами было опубликовано много модификаций времени-частотных представлений сигналов.
В конце 70-х инженер-геофизик Морли (Jean Morlet) столкнулся с проблемой анализа сигналов, которые характеризовались высокочастотной компонентой в течение короткого промежутка времени и низкочастотными колебаниями при рассмотрении больших временных масштабов. Оконные преобразования позволяли проанализировать либо высокие частоты в коротком окне времени, либо низкочастотную компоненту, но не оба колебания одновременно. В результате был предложен подход, в котором для различных диапазонов частот использовались временные окна различной длительности. Оконные функции получались в результате растяжения-сжатия и смещения по времени гаусиана. Морли назвал эти базисные функции вейвлетами (wavelets) - компактными волнами. В дальнейшем благодаря работам Мейера (Yves Meyer), Добеши (Ingrid Daubechies), Койфмана (Ronald Coifman), Маллы (Stephane Mallat) и других теория вейвлетов приобрела свое современное состояние.
|
|
|
Среди российских ученых, работавших в области теории вейвлетов, необходимо отметить С.Б. Стечкина, И.Я. Новикова, В.И. Бердышева.
МНОГОМАСШТАБНЫЙ АНАЛИЗ И ВЕЙВЛЕТЫ
Определение 1. Многомасштабный анализ ( multiresolutional analysis) – разложение гильбертова пространства L2(Rd), d ³1, в последовательность замкнутых подпространств
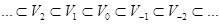 , (1.1)
, (1.1)
обладающих следующими свойствами:
|
|
|
1. 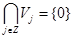 , и
, и 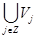 полно в L2(Rd),
полно в L2(Rd),
2. Для любого f Î L2(Rd), для любого j Î Z, f( x) Î Vj тогда и только тогда, когда
f(2 x) Î Vj-1,
3. Для любого f Î L2(Rd), для любого k Î Zd, f( x) Î V0 тогда и только тогда, когда f( x- k) Î V0,
4. Существует масштабирующая ( scaling) функция j Î V0, что { j( x- k)} k Î Z d образует
базис Ритца в V0.
Для ортонормальных базисов можно переписать свойство 4 в виде:
4’. Существует масштабирующая функция j Î V0, что { j( x- k)} k Î Z d образует ортонормальный базис в V0.
Определим подпространство Wj как ортогональное дополнение к Vj в Vj-1,
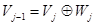 , (1.2)
, (1.2)
и представим пространство L2(Rd) в виде прямой суммы
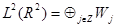 (1.3)
(1.3)
Выбирая масштаб n, можем заменить последовательность (1.1) следующей последовательностью:
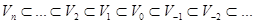 (1.4)
(1.4)
и получить
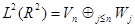 (1.5)
(1.5)
Если имеем конечное число масштабов, то, не нарушая общности, можно положить j=0 и рассматривать
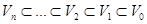 , V0 Î L2(Rd) (1.6)
, V0 Î L2(Rd) (1.6)
вместо (1.4). В числовой реализации подпространство V0 конечномерно.
Функция j - так называемая масштабирующая (скейлинг-) функция. С ее помощью можно определить функцию y - вейвлет - такую, что набор { y( x- k)} k Î Z образует ортонормальный базис в W0. Тогда
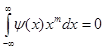 , m=0.. M-1. (1.7)
, m=0.. M-1. (1.7)
Из свойства 4’ непосредственно следует, что, во-первых, функция j может быть представлена в виде линейной комбинации базисных функций пространства V-1 . Так как функции { j j, k( x)=2- j/2 j(2- j x- k)} k Î Z образуют ортонормальный базис в Vj, то имеем
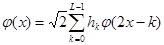 . (1.8)
. (1.8)
Вообще говоря, сумма в выражении (1.8) не обязана быть конечной. Можно переписать (1.8) в виде
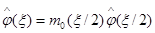 , (1.9)
, (1.9)
где
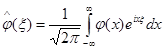 , (1.10)
, (1.10)
а 2p-периодическая функция m0 определяется следующим образом:
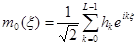 . (1.11)
. (1.11)
Во-вторых, ортогональность { j( x- k)} k Î Z подразумевает, что
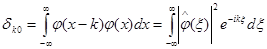 (1.12)
(1.12)
и значит
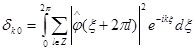 (1.13)
(1.13)
и 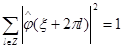 . (1.14)
. (1.14)
Используя (1.9), получаем
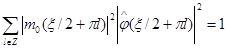 (1.15)
(1.15)
и, рассматривая сумму в (1.15) по четным и нечетным индексам, имеем
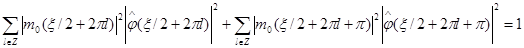 . (1.16)
. (1.16)
Используя 2p-периодичность функции m0 и (1.14), после замены x/2 на x, получаем необходимое условие
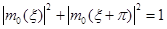 (1.17)
(1.17)
для коэффициентов hk в (1.11). Заметив, что
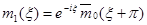 (1.18)
(1.18)
и определив функцию y следующим образом:
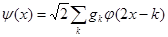 , (1.19)
, (1.19)
где
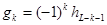 , k=0,…, L-1 , (1.20)
, k=0,…, L-1 , (1.20)
или преобразование Фурье для y
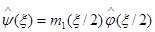 , (1.21)
, (1.21)
где
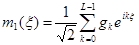 , (1.22)
, (1.22)
можно показать, что при каждом фиксированном масштабе j ÎZ вейвлеты
{ y j, k( x)=2- j/2 y(2- j x- k)} k Î Z образуют ортонормальный базис пространства Wj.
Равенство (1.17) определяет пару квадратурных зеркальных фильтров (quadrature mirror filters, QMF) H и G, где 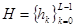 и
и 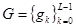 . Коэффициенты QMF H и G вычисляются с помощью решения системы алгебраических уравнений. Число L коэффициентов фильтра в (1.11) и (1.22) связано с числом исчезающих моментов М, и всегда четно.
. Коэффициенты QMF H и G вычисляются с помощью решения системы алгебраических уравнений. Число L коэффициентов фильтра в (1.11) и (1.22) связано с числом исчезающих моментов М, и всегда четно.
Выбранный фильтр Н полностью определяет функции j и y и, таким образом, многомасштабный анализ. Кроме того, в правильно построенных алгоритмах значения функций j и y почти никогда не вычисляются. Благодаря рекурсивному определению вейвлетного базиса, все операции проводятся с квадратурными зеркальными фильтрами H и G, даже если в них используются величины, связанные с j и y.
ОПЕРАТОРЫ
Сжатие операторов или, другими словами, представление их в разреженном виде в ортонормированном базисе непосредственно влияет на скорость вычислительных алгоритмов.
Нестандартная форма оператора Т с ядром K( x, y) достигается вычислением следующих выражений:
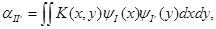 (4.1)
(4.1)
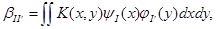 (4.2)
(4.2)
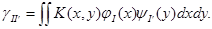 (4.3)
(4.3)
4.1 Оператор d / dx в вейвлетном базисе
Нестандартные формы некоторых часто используемых операторов могут быть вычислены явно. Построим нестандартную форму оператора d/ dx. Матричные элементы 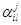 ,
, 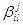 ,
, 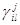 матриц
матриц 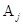 ,
, 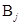 ,
, 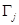 и
и 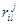 матрицы
матрицы 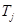 , где i, l, j Î Zдля оператора d/dx легко вычисляются как
, где i, l, j Î Zдля оператора d/dx легко вычисляются как
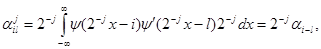 (4.4)
(4.4)
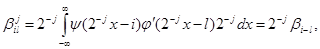 (4.5)
(4.5)
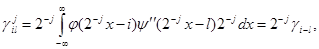 (4.6)
(4.6)
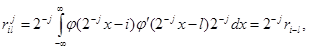 (4.7)
(4.7)
где
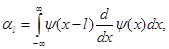 (4.8)
(4.8)
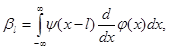 (4.9)
(4.9)
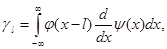 (4.10)
(4.10)
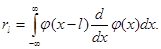 (4.11)
(4.11)
Кроме того, используя (1.8) и (1.19), имеем
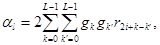 (4.12)
(4.12)
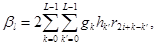 (4.13)
(4.13)
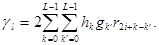 (4.14)
(4.14)
Таким образом представление d/ dx полностью определяется величинами 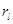 или, другими словами, отображением d/ dx на подпространство V0.
или, другими словами, отображением d/ dx на подпространство V0.
Предложение 4.1. 1. Если существует интеграл (4.11), тогда коэффициенты 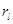 , l Î Zв (5.8) удлвлетворяют следующей системе линейных алгебраических уравнений:
, l Î Zв (5.8) удлвлетворяют следующей системе линейных алгебраических уравнений:
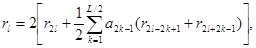 (4.15)
(4.15)
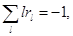 (4.16)
(4.16)
где
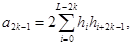
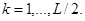 (4.17)
(4.17)
2. Если 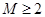 , тогда система (4.15)-(4.16) имеет единственное решение с конечным числом ненулевых
, тогда система (4.15)-(4.16) имеет единственное решение с конечным числом ненулевых 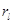 , а именно с
, а именно с  и
и 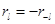 .
.
Замечание. Если М=1, тогда система (4.15)-(4.16) имеет единственное решение, но интеграл (4.11) может не быть абсолютно сходящимся. Для базиса Хаара ( 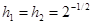 )
) 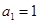 ,
, 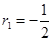 мы получаем простейший конечный дифференциальный оператор
мы получаем простейший конечный дифференциальный оператор 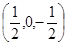 .
.
Замечание 2. Заметим, что выражения (4.12) и (4.13) для 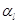 и
и 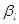 (
( 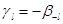 ) могут быть упрощены с помощью смены порядка суммирования в (5.10) и (5.11) и введения коэффициентов корреляции
) могут быть упрощены с помощью смены порядка суммирования в (5.10) и (5.11) и введения коэффициентов корреляции 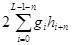 ,
, 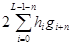 и
и 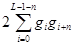 . Выражение для
. Выражение для 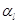 особенно просто:
особенно просто: 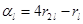 .
.
Для доказательства Предложения 4.1 можно обратиться к [2].
Для решения системы (4.15)-(4.16) можно также воспользоваться итерационным алгоритмом. Начать можно с 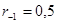 и
и 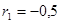 , а дальше итерировать, используя (4.15) для вычисления
, а дальше итерировать, используя (4.15) для вычисления 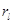 .
.
4.2 Оператор d n / dx n в вейвлетном базисе
Так же как и для оператора d/ dx, нестандартная форма оператора dn/ dxn полностью определяется своим отображением на подпространство V0, т.е. коэффициентами
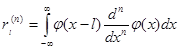 , l Î Z, (4.18)
, l Î Z, (4.18)
если интеграл существует.
Предложение 4.2. 1. Если интеграл в выражении (4.18) существует, тогда коэффициенты 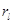 , l Î Zудовлетворяют следующей системе линейных алгебраических уравнений
, l Î Zудовлетворяют следующей системе линейных алгебраических уравнений
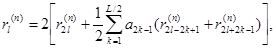 (4.19)
(4.19)
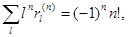 (4.20)
(4.20)
где 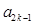 дано в формуле (4.17).
дано в формуле (4.17).
2. Пусть M ≥ ( n+1)/2, где М – число исчезающих моментов. Если интеграл в (4.18) существует, тогда система (4.19)-(4.20) имеет единственное решение с конечным числом нулевых коэффициентов 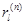 , а именно
, а именно 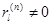 для
для 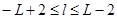 . Также для четных n
. Также для четных n
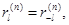 (4.21)
(4.21)
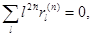
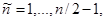 (4.22)
(4.22)
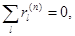 (4.23)
(4.23)
а для нечетных n
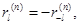 (4.24)
(4.24)
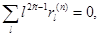
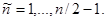 (4.25)
(4.25)
Замечание 3. Если M ≥ ( n+1)/2, тогда решение линейной системы в Предложении 2 может существовать, когда интеграл в (4.18) не является абсолютно сходящимся.
Дата добавления: 2019-07-15; просмотров: 160; Мы поможем в написании вашей работы! |

Мы поможем в написании ваших работ!
