Графіки функцій комплексної змінної
Комплексні числа можна трактувати як точки на площині. Тоді множину Мандельброта можна побудувати у просторі 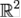 .
.
Взагалі, графік дійсної функції можна побудувати в двомірному просторі (2D), на площині xOy. Це багатьом знайомо й звично(мал.15 а,б):
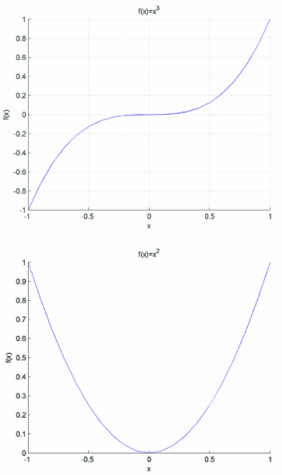
Мал.15(а,б)
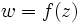 Графік комплексної функції можна було б побудувати в чотиривимірному (4D) просторі (дві координати потрібно для зображення
Графік комплексної функції можна було б побудувати в чотиривимірному (4D) просторі (дві координати потрібно для зображення 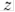 , і дві – для
, і дві – для 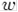 ).
).
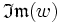
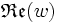
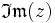
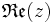 На жаль, переважна більшість людей стикаються з серйозними проблемами при уяві чотиривимірного простору... Тому, одне з хитрощів, зазвичай вживане, полягає в наступному: графік будується в тривимірному (3D) просторі. Вісь Ox відповідає за , вісь Oy – за , вісь Oz – за…….. Для зображення використовується колір отриманої 3D-крапки. Колір береться із заздалегідь сформованої кольорової шкали (градієнта).
На жаль, переважна більшість людей стикаються з серйозними проблемами при уяві чотиривимірного простору... Тому, одне з хитрощів, зазвичай вживане, полягає в наступному: графік будується в тривимірному (3D) просторі. Вісь Ox відповідає за , вісь Oy – за , вісь Oz – за…….. Для зображення використовується колір отриманої 3D-крапки. Колір береться із заздалегідь сформованої кольорової шкали (градієнта).
Ось декілька прикладів (мал.16 а,б) для 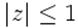 :
:
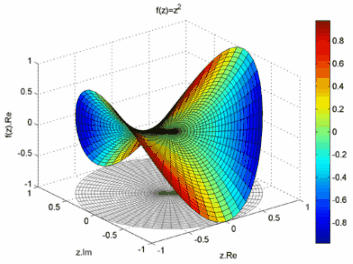
а) 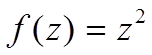
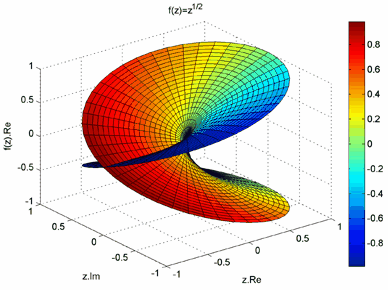
б) 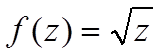
Мал.16 (а,б)
Для наочності під отриманою «поверхнею» зображено множина значень 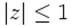 ( («кругла тінь»).
( («кругла тінь»).
Формули побудови фракталів
2.7.1 Різновид алгебраїчних фракталів — басейни Ньютона (мал.17).
p(z) = 0, p(z) = 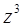 − 1,
− 1,
які будуються за формулою:
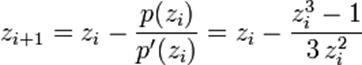
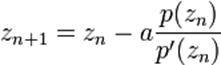
Узагальнена формула , де a — будь-яке комплексне число.

Множина Жюліа та Мандельброта
Позначимо через 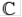 площину комплексних чисел, а через
площину комплексних чисел, а через  — риманову сферу
— риманову сферу  . Розглянемо процес
. Розглянемо процес 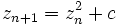 , де
, де 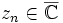 та
та 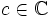 . Взявши будь-яке число
. Взявши будь-яке число 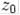 , піднесемо до квадрату та додамо константу для того, щоб отримати
, піднесемо до квадрату та додамо константу для того, щоб отримати 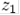 ; потім повторимо розрахунки для того, щоб отримати
; потім повторимо розрахунки для того, щоб отримати 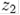 ,
, 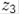 і так далі.
і так далі.
|
|
|
Почнемо з найпростішого із можливих значень константи  , тобто
, тобто 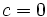 . Тоді при кожній ітерації підраховується точний квадрат числа:
. Тоді при кожній ітерації підраховується точний квадрат числа: 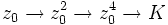 . У залежності від значення розглядається три випадки:
. У залежності від значення розглядається три випадки:
1. Якщо 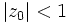 , тоді числа отримуються все менші та менші, їх послідовність прямує до нуля.
, тоді числа отримуються все менші та менші, їх послідовність прямує до нуля.
2. Якщо 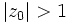 , тоді числа отримуються все більші та більші, прямуючи до нескінченності.
, тоді числа отримуються все більші та більші, прямуючи до нескінченності.
3. Якщо 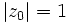 , тоді точки продовжують залишатися на відстані 1 від нуля. Їх послідовності лежать на границі двох областей тритягання, у данному випадку на колі (мал.18) з одиничним радіусом та центром у нулі.
, тоді точки продовжують залишатися на відстані 1 від нуля. Їх послідовності лежать на границі двох областей тритягання, у данному випадку на колі (мал.18) з одиничним радіусом та центром у нулі.

Мал.18
Ситуація така: площина ділиться на дві зони впливу, а границя між ними є просто коло.
Сюрприз починається, коли ми візьмемо значення параметру  не дорівнює нулю, наприклад
не дорівнює нулю, наприклад 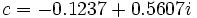 . У цьому випадку для послідновності присутні також три вищеперелічених випадків, але внутрішня точка, до якої прямує послідовність, вже не є нулем, а границя вже не є плоскою, вона надто крива(мал.19). Саме це Б. Мандельброт назвав фрактальной структурой такої границі.
. У цьому випадку для послідновності присутні також три вищеперелічених випадків, але внутрішня точка, до якої прямує послідовність, вже не є нулем, а границя вже не є плоскою, вона надто крива(мал.19). Саме це Б. Мандельброт назвав фрактальной структурой такої границі.

Мал.19
Однією з таких характерних особливостей такої границі є її самоподібність. Якщо взяти будь-яку частину границі, то можна побачити, що вона зустрічається в різних місцях границі та мають різні розміри. Границі такого виду в математиці називають множинами Жюліа.
|
|
|
Різноманітні значення параметру 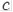 можуть створювати різноманітні множини Жюліа, причому найменші зміни цього параметру нерідко призводять до суттєвих метаморфоз.
можуть створювати різноманітні множини Жюліа, причому найменші зміни цього параметру нерідко призводять до суттєвих метаморфоз.

Деякі множини Жюліа зв’язні, інші являють собою «пилевидні» канторові множини(мал.20 а,б,в,г).
Існує правило, що з’ясовує вид множини Жюліа. Воно залежить від параметру  та пов’язано з зображенням множини Мандельброта. Множина всіх точок
та пов’язано з зображенням множини Мандельброта. Множина всіх точок 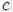 , для яких ітерації
, для яких ітерації 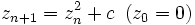 залишаються обмеженими при
залишаються обмеженими при 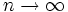 , називається множиною Мандельброта (мал.21).
, називається множиною Мандельброта (мал.21).
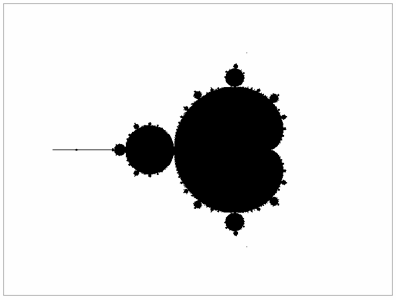
Мал.21
Цікаво, що всі значення  , при яких множини Жюлиа зв’язні, належать множині Мандельброта, тому останнє може бути визначеним і як множина всіх значень параметру
, при яких множини Жюлиа зв’язні, належать множині Мандельброта, тому останнє може бути визначеним і як множина всіх значень параметру  , при яких множина Жюліа зв’язна.
, при яких множина Жюліа зв’язна.
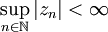
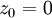 Сукупність елементів
Сукупність елементів 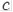 поля коплексних чисел, для яких послідовність:
поля коплексних чисел, для яких послідовність: 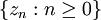 , що визначена ітераційно за правилом
, що визначена ітераційно за правилом 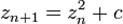 , де …… задовольняє умову . Наприклад множина Мандельброта (мал.22 а,б,в,г,д,е).
, де …… задовольняє умову . Наприклад множина Мандельброта (мал.22 а,б,в,г,д,е).

|
|
|
а) 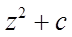 б)
б) 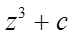 в)
в) 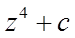

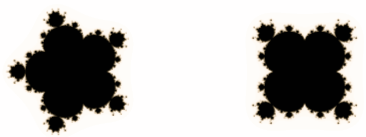
г)  д)
д) 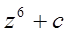 е)
е) 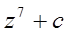
Мал.22
Висновок
Фрактал є однією з багатьох складових частин певної субстанції, тому зникнення однієї з таких складових призводить до втрати візуальної гармонії, що людське око розпізнає одразу. Присутність фрактала з першого погляду можна і не помітити, якщо не заглиблюватись у досконале вивчення математики. Ця наука, дійсно, не має меж і постійно спонукає до різноманітних досліджень.
Фрактал — це математична величина, що зустрічається досить часто. Але якщо добре не придивитися, його можна і не побачити. Абсолютно точна, алгебраїчна величина, яка творить собою неймовірні фігури, візерунки та складає цікаві орнаменти, що ми зустрічаємо кожного дня. Це і листя папороті, і маленькі сніжинки та ще багато іншого.
Галілео Галілей у 1623 році писав: “Вся наука записана у цій великій книзі, — я маю на увазі Всесвіт, — що завжди відкрита для нас, але яку неможливо зрозуміти, не навчившись розуміти мову, на якій вона написана, а написана вона на мові математики, і її лутерами є трикутники, кола і інші геометричні фігури, без яких людині не можливо розібрати жодного її слова; без них вона подібна блукаючому в пітьмі…”
Поняття фрактала змінило багато традиційних уявлень про геометрію, а в історії розвитку математики введення цього поняття стало переломним моментом. З кожним роком поняття фрактала стає відоме все більш широкому колу людей. І зараз цей термін важко залишити без належної уваги. У природі є багато чого, що має прямий зв’язок до цього терміну.
|
|
|
Займаючись цією темою напротязі двох років, я більш широко дізнався про об’єкт дослідження: його властивості, способи створення та використання. З алгебраїчних фракталів я звернув увагу на три основні їх види: множину Мандельброта, множину Жюліа, дракон Хартера-Хейтуея, які відрізняються один від одного за побудовою та своїми загальними формулами створення, на мою думку, найбільше досліджені в наш час. За допомогою їх з’являється більшість новостворених фракталів.
Знайшовши збірник зображень фракталів, що були створені небагато років тому, і серед яких провели конкурс на найкращий малюнок, мене дуже вразило розмаїття кольорів та фантазія людей. Мені стало відомо, яким чином вони створюються в наш час, що цією темою зацікавлені люди, яким до вподоби неординарне художнє мистецтво, що не рідко втілюється у комп’ютерній графіці.
Сподіваюсь, що і після закінчення гімназії, у мене залишиться велике бажання продовжити досліджувати загальні формули побудови фракталів і за допомогою цих формул створювати нові фрактали та захоплюватися їхньою незрівнянною красою.
Використана література
1. Мандельброт Б. Фрактальная геометрия природы. — М.: «Институт компьютерных исследований», 2002.
2. Пайтген Х.-О., Рихтер П. Х. Красота фракталов. — М.: «Мир», 1993.
3. Федер Е. Фракталы. — М: «Мир», 1991.
4. Фоменко А. Т. Наглядная геометрия и топология. — М.: изд-во МГУ, 1993.
5. Фракталы в физике. Труды 6-го международного симпозиума по фракталам в физике, 1985. — М.: «Мир», 1988.
6. Шредер М. Фракталы, хаос, степенные законы. Миниатюры из бесконечного рая. — Ижевск: «РХД», 2001.
7. Мандельброт Бенуа, Ричард Л. Хадсон (Не)послушные рынки: фрактальная революция в финансах = The Misbehavior of Markets. — М.: «Вильямс», 2006. — С. 400. ISBN 5-8459-0922-8
8. http://en.wikipedia.org/wiki/Fractal
9. http://en.wikipedia.org/wiki/Mandelbrot_set
10. http://en.wikipedia.org/wiki/Julia_set
11. http://en.wikipedia.org/wiki/Newton_fractal
12. http://en.wikipedia.org/wiki/Fractal_art
13. http://commons.wikimedia.org/wiki/Fractal
14.http://en.wikipedia.org/wiki/Fractal_landscape 15.http://ru.wikipedia.org/wiki/%D0%A4%D1%80%D0%B0%D0%BA%D1%82%D0%B0%D0%BB
16. http://www.fractalus.com/
Дата добавления: 2019-07-15; просмотров: 179; Мы поможем в написании вашей работы! |

Мы поможем в написании ваших работ!
