О диагональных формах и оценка снизу числа классов в роде.

⇐ ПредыдущаяСтр 3 из 3

В этом параграфе мы получим одну оценку снизу для числа классов в роде неопределенных бинарных квадратичных форм. Сначала введем соответствующие понятия.

Определение 1. Целое число 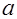, не делящееся на простое число 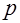называется квадратичным вычетом по модулю простого числа, если число 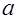сравнимо с квадратом некоторого целого числа по модулю 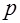, т.е. 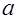- квадратичный вычет по модулю 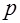, если сравнение 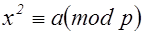имеет решение; в противном случае число 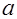называется квадратичным невычетом по модулю 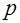. В теории квадратичных вычетов очень полезно использование так называемого символа Лежандра.

Определение 2. Символом Лежандр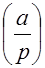а числа 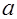по простому модулю 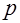, которое определяется следующим соотношением

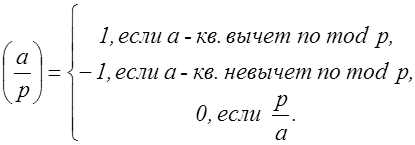
Приведем некоторые основные свойства символа Лежандра, которые нам понадобятся.

Свойство 1. 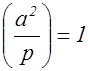, если .

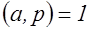Свойство 2. Если 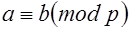, то 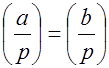(свойство периодичности).

Свойство 3. 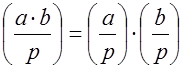(свойство мультипликативности)

Свойство 4. 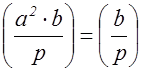, если .

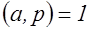Определим теперь понятие рода квадратичных форм, впервые введенное Гауссом. Совокупность классов собственно примитивного порядка данного дискриминанта 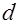Гаусс в своей арифметической теории квадратичных форм разделяет на ряды, относя в один и тот же род все те классы, формы которых имеют и тот же «характер». Под характером примитивной формы или примитивного класса форм Гаусс понимает следующее.

Пусть 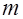- простой делитель дискриминанта 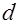, и пусть число всех этих различных модулей 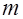равно 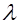. Можно показать, что если 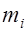- один из этих 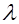модулей, то для всех чисел 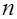, представимых данной собственно примитивной формой дискриминанта 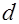и взаимно простых с 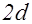, символы Лежандра 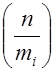имеют одно и то же значение. В самом деле, пусть

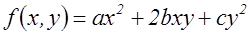- собственно примитивная форма дискриминанта 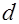и 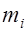- любой нечетный простой делитель числа 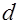и 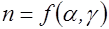, 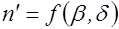- два числа, представляемых формой 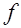и не делящихся на 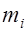. Подстановка 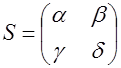определителя 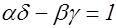переводит 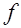в форму 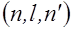(см. соотношения (3) §1), причем 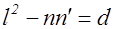, откуда 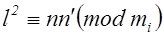, т.е. в силу определения символа Лежандра имеем 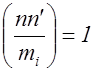. Из этого равенства в очередь на основании свойств 3 и 4следует, что 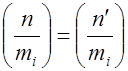. Итак, символ Лежандра 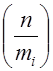имеет одно и то же значение для всех чисел 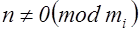, представляемых формой 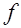. Выпишем эти символы Лежандра, которые все равны 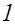или 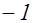для всех 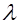указанных модулей 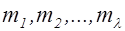, взятых в определенном выбранном порядке. Тогда для данной квадратичной формы получается некоторая определенная последовательность 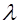чисел, равных 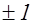. Эта последовательность чисел, равных 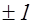и называется характером рассматриваемой собственно примитивной бинарной квадратичной формы дискриминанта 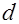или характером класса этой формы.

Так как число всех различных последовательностей, составленных из 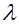членов, равных 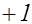или 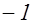равно 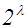, то число различных характеров форм данного дискриминанта, а следовательно и число родов не больше, чем 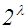. Чтобы решить вопрос о точном числе родов Гаусс вводит в рассмотрение операции композиции классов и композиции родов квадратичных форм. Не вдаваясь в эту сложную теорию Гаусса, мы приведем его результаты о числе родов и о числе классов в каждом роде.

Теорема 1 (Гаусс). Число родов бинарных квадратичных форм в данном собственно примитивном порядке дискриминанта 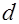равно 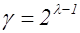, где 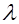определяется следующими условиями:

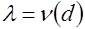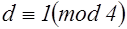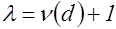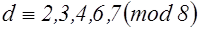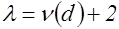при ,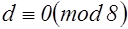

при этом 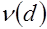- число различных простых делителей числа .

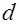Теорема 2 (Гаусс). Каждый род собственно примитивного порядка содержит одно и то же число классов, т.е.

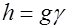где 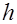- число всех классов, 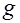- число классов в каждом роде и 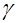-число родов.

Перейдем теперь после такого предварительного обсуждения к изложению результатов данного параграфа. Следующая теорема устанавливает существование неэквивалентных диагональных квадратичных форм данного дискриминанта.

Теорема 3. Диагональная форма 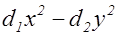дискриминанта 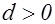не эквивалентна никакой другой диагональной форме того же дискриминанта.

Доказательство. Допустим, что диагональная форма

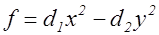(1)

дискриминанта 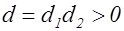собственно эквивалентна другой диагональной форме

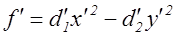(2)

того же дискриминанта 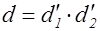. Тогда найдется целочисленная унимодулярная подстановка 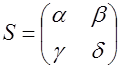, которая переводит форму 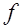в форму .

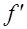Имеем

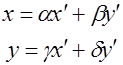(3)

где

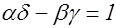(4)

Подставляя (3) в (1), получим

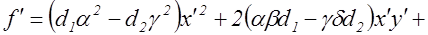
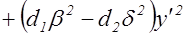Но так как, мы требуем, чтобы форма 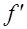была тоже диагональной, то

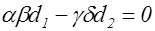. (5)

Тогда форма 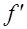перепишется в следующем виде

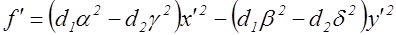. (6)

Далее, так как 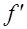имеет тот же дискриминант, что и форма 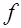, то

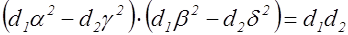, (7)

или что то же самое

;

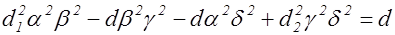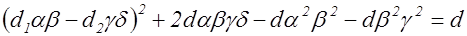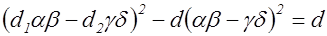(8)

откуда с учетом (5), полученное соотношение (8) перепишется в виде

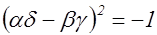что противоречит условию (4).

Значит наше допущение о том, что диагональная форма эквивалентна другой диагональной форме того же дискриминанта неверно.

Теорема 3 доказана.

Полученную теорему 3 можно применить к оценке снизу числа классов в роде неопределенных бинарных квадратичных форм собственно примитивного порядка.

Теорема 4. Если для каждого квадратного делителя 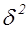дискриминанта 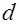выполнены условия:

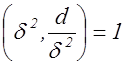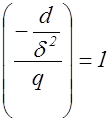
НОД , 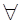простого ,

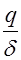то для числа 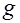классов неопределенных квадратичных форм дискриминанта 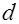в каждом роде собственно примитивного порядка выполняется неравенство

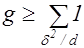Доказательство. Пусть 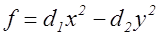- собственно примитивная форма дискриминанта 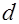, т.е. НОД 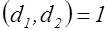и пусть она представляет целое число 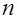, т.е. 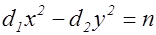при некоторых целых 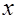и 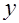. Будем считать, что 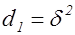, где 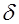- целое число. Тогда символ Лежандра числа 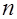по простому делителю 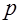числа 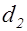равен

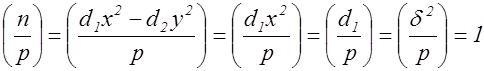Далее 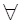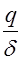по условию имеем

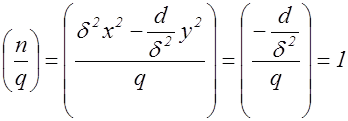Полученное означает, что форма 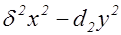принадлежит главному роду (род называется главным, если характеры его форм равны 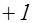). Число таких форма равно числу квадратных делителей 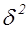дискриминанта 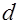с условием НОД 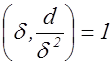и все они эквивалентны по теореме 3. Поэтому для числа классов 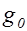в главном роде справедлива оценка снизу

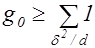с условием .

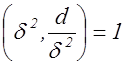В силу теоремы 2 Гаусса такая же оценка справедлива и для числа классов всех остальных родов.

Теорема 4 доказана.

ЛИТЕРАТУРА.

1. Венков Б.А. Элементарная теория чисел. М-Л., 1937, с. 218

2. Гаусс К.Ф. Труды по теории чисел. Изд-во АН СССР, М., 1959, с. 978

3. Чандрасекхаран К. Введение в аналитическую теорию чисел. Изд-во «Мир», М., 1974, с. 187

4. Виноградов И.М. Основы теории чисел. Изд-во «Наука», М., 1972 с. 267

5. Виноградов И.М. Метод тригонометрических сумм в теории чисел. М., «Наука», 1980, с. 144

6. Бухштаб А.А. Теория чисел. М., 1966, с. 384

Дата добавления: 2019-07-15; просмотров: 115; Мы поможем в написании вашей работы!

Поделиться с друзьями:

⇐ Предыдущая 1 23

Мы поможем в написании ваших работ!