Применение симплекс-метода для оптимальной организации
КОНТРОЛЬНАЯ РАБОТА
По дисциплине
« ОПТИМИЗАЦИЯ ОРГАНИЗАЦИОННЫХ РЕШЕНИЙ»
Задание №1
Решение задачи об оптимальном направлении капиталовложений в строительную отрасль и оптимизации поставки строительных грузов
Определить наиболее экономичный вариант прироста мощности (строительства или реконструкции) и одновременно рассчитать оптимальный план перевозок строительной продукции до потребителя.

Решение
Составим базисные планы:
а) метод северо-западного угла

Значение целевой функции:
L1 = 160 х 15 + 20 х 3 + 60 х 10 + 180 х 5 + 40 х 16 + 40 х 0 =
= 2 400 + 60 + 600 + 900 + 640 + 0 = 4 600 у. е.
б) метод двойного предпочтения
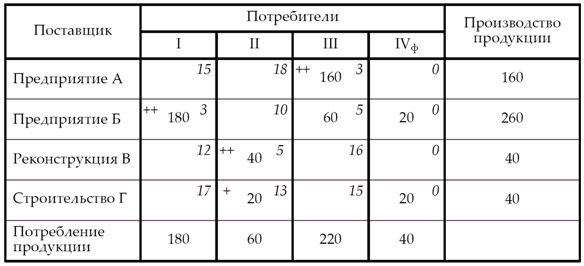
Значение целевой функции:
L2 = 180 х 3 + 160 х 3 + 60 х 5 + 20 х 0 + 40 х 5 + 20 х 13 + 20 х 0 =
= 540 + 480 + 300 + 0 + 200 + 260 + 0 = 1 780 у. е.
в) метод аппроксимации Фогеля

Значение целевой функции:
L3 = 160 х 3 + 180 х 3 + 20 х 10 + 60 х 5 + 40 х 5 + 40 х 0 =
= 480 + 540 + 200 + 300 + 200 + 0 = 1 720 у. е.
Проведем проверку матрицы на вырождение:
N – число занятых клеток матрицы, N = 6.
N = m + n – 1 = 4 + 4 – 1 = 7.
6 ≠ 7.
Следовательно, матрица – вырожденная, поэтому в одну из свободных ячеек в зоне вырождения вводим условную нулевую поставку груза.

Оптимальный план находим на основании базисного плана, построенного методом аппроксимации Фогеля, так как этот план имеет минимальную целевую функцию.
Проверим матрицу на оптимальность с помощью потенциалов строк u и столбцов v.
Потенциалы определим по занятым клеткам матрицы, тем самым соблюдая условие оптимальности (cij = u ij + vij).

Произведем проверку свободных клеток базисного плана на оптимальность.
| Коды свободных клеток | Δ = cij – ( vij + uij) | Примечание |
| A-I | 15 – (1 + 0) = 15 | >0 |
| A-II | 18 – (8 + 0) = 10 | >0 |
| A-IV | 0 – (-2 + 0) = 2 | >0 |
| B-I | 12 – (1 – 3) = 14 | >0 |
| B-III | 16 – (3 – 3) = 16 | >0 |
| B-IV | 0 – (-2 + 2) = 0 | =0 |
| Г-I | 17 – (1 + 2) = 14 | >0 |
| Г-II | 13 – (8 + 2) = 3 | >0 |
| Г-III | 15 – (3 + 2) = 10 | >0 |
В данном случае все значения Δ ≥ 0, следовательно, составленный план неоптимален, переходим к улучшенному плану перевозок. В этом случае среди незагруженных клеток, для которых Δ ≥ 0, находим клетку с наибольшей величиной превышения стоимости (B-III).
Строим замкнутый контур, начиная перемещаться из потенциальной клетки.

Контур распределения:
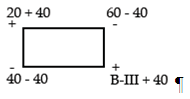
Составим новый план распределения.

Его целевая функция:
L4 = 160 х 3 + 180 х 3 + 60 х 10 + 20 х 5 + 40 х 16 + 40 х 0 =
= 480 + 540 + 600 + 100 + 640 + 0 = 2 360 у. е.
Проверяем полученную матрицу на оптимальность.
| Коды свободных клеток | Δ = cij – ( vij + uij) | Примечание |
| A-I | 15 – (1 + 0) = 15 | >0 |
| A-II | 18 – (8 + 0) = 10 | >0 |
| A-IV | 0 – (-2 + 0) = 2 | >0 |
| B-I | 12 – (1 – 3) = 14 | >0 |
| B-II | 5 – (8 + 13) = -16 | <0 |
| B-IV | 0 – (-2 + 13) = -11 | <0 |
| Г-I | 17 – (1 + 2) = 14 | >0 |
| Г-II | 13 – (8 + 2) = 3 | >0 |
| Г-III | 15 – (3 + 2) = 10 | >0 |
Наибольшее превышение стоимости наблюдаем в клетке А-I.

Контур распределения:

Новый план распределения:

Его целевая функция:
L4 = 160 х 15 + 20 х 3 + 60 х 10 + 180 х 5 + 40 х 16 + 40 х 0 =
= 2 400 + 60 + 600 + 900 + 640 + 0 = 4 600 у. е.
Проверяем полученную матрицу на оптимальность.
| Коды свободных клеток | Δ = cij – ( vij + uij) | Примечание |
| A-II | 18 – (22 + 0) = -4 | <0 |
| A-III | 3 – (17 + 0) = -14 | <0 |
| A-IV | 0 – (12 + 0) = -12 | <0 |
| B-I | 12 – (15 + 13) = -16 | <0 |
| B-II | 5 – (22 + 13) = -30 | <0 |
| B-IV | 0 – (12 + 13) = -25 | <0 |
| Г-I | 17 – (15 - 12) = 14 | >0 |
| Г-II | 13 – (22 - 12) = 3 | >0 |
| Г-III | 15 – (17 - 12) = 10 | >0 |
Данный план распределения продукции является наиболее эффективным из представленных, хотя не до конца оптимальным.
Вывод
Поскольку в оптимальном плане прирост мощности 40 тыс. у. е. продукции за счет строительства отнесен на фиктивного потребителя, то строительство нового цеха или пристройку цеха к действующему следует считать нецелесообразным, и капитальные вложения необходимо направить на реконструкцию действующего предприятия.
Задание №2
Применение симплекс-метода для оптимальной организации
Ремонтно-строительных работ
Определить максимальное количество квартир в домах кирпичных и крупнопанельных, которые можно отремонтировать из имеющихся ресурсов.
| Ресурсы | Потребность в ресурсах на одну квартиру | |||
| Наименование | Количество | кирпичный дом | панельный дом | |
| Арматура, т | 900 | 0,6 | 1,3 | |
| Пиломатериалы, м3 | 520 | 0,8 | 0,3 | |
| Цемент, т | 7 000 | 5 | 9 | |
| Керамическая плитка, тыс. шт. | 400 | 0,5 | -- | |
| Трудозатраты, чел. дн. | 55 000 | 70 | 50 | |
Решение
Для решения данной задачи применим симплекс-метод.
Обозначим:
Х1 – искомое количество квартир в кирпичном доме;
Х2 – искомое количество квартир в панельном доме.
Целевая функция:
L = Х1 + Х2  max
max
Ограничениями будут неравенства, полученные на основании исходных данных:
1. Арматура 0,6Х1 + 1,3 Х2 ≤ 900;
2. Пиломатериалы 0,8Х1 + 0,3 Х2 ≤ 520;
3. Цемент 5Х1 + 9Х2 ≤ 7 000;
4. Керамическая плитка 0,5Х1 ≤ 400;
5. Трудозатраты 70Х1 + 50Х2 ≤ 55 000;
6. Х1 ≥ 0;
7. Х2 ≥ 0.
Поскольку имеется только два неизвестных, то применим геометрическое решение. Для удобства построений преобразуем не равенства.
1. 6Х1 + 13 Х2 ≤ 9 000;
2. 8Х1 + 3 Х2 ≤ 5 200;
3. 5Х1 + 9Х2 ≤ 7 000;
4. 5Х1 ≤ 4 000;
5. 7Х1 + 5Х2 ≤ 5 500;
6. Х1 ≥ 0;
7. Х2 ≥ 0.
Геометрически ограничения неравенств выражаются в виде открытых полуплоскостей, ограниченных осями координат и линиями, описываемыми равенствами, полученными из выражений ограничений:
1. 6Х1 + 13 Х2 = 9 000;
2. 8Х1 + 3 Х2 = 5 200;
3. 5Х1 + 9Х2 = 7 000;
4. 5Х1 = 4 000;
5. 7Х1 + 5Х2 = 5 500.
Нанесем эти линии на график.

В целом условиям неравенств удовлетворяет заштрихованная область. Оптимальное решение находится на контуре этой фигуры в одной из узловых точек и определяется совместным рассмотрением выражений:
L = Х1 + Х2  max
max
6Х1 + 13 Х2 = 9 000;
8Х1 + 3 Х2 = 5 200;
5Х1 + 9Х2 = 7 000;
5Х1 = 4 000;
7Х1 + 5Х2 = 5 500.
Возрастание целевой функции направлено слева вверх под углом 45°, и последней точкой в допустимой области будет точка 1 или 2.
Точка 1 получена пересечением прямых, описываемых равенствами:
6Х1 + 13 Х2 = 9 000;
7Х1 + 5Х2 = 5 500.
Решая эти равенства, найдем координаты точки 1: Х1 = 200; Х2 = 600.
Аналогично найдем координаты точки 2 из выражений:
7Х1 + 5Х2 = 5 500;
8Х1 + 3 Х2 = 5 200.
Координаты точки 2: Х1 = 498; Х2 = 406.
Найдем, какая из указанных точек дает большее значение целевой функции.
L 1 = Х1 + Х2 = 200 + 600 = 800;
L 2 = Х1 + Х2 = 498 + 406 = 904.
Оптимальной является точка 2, дающая 498 квартир в кирпичных домах и 406 в панельных. При этом будут полностью исчерпаны такие ресурсы как пиломатериалы и трудозатраты.
Использование остальных ресурсов найдем, решая вышеуказанные равенства при зафиксированных значениях Х1 = 498; Х2 = 406.
0,6 х 498 + 1,3 х 406 = 299 + 528 = 827 (арматура), неиспользовано 73 т арматуры.
5 х 498 + 9 х 406 = 2 490 + 3 654 = 6 144 (цемент), неиспользовано 856 т.
0,5 х 498 = 249 тыс. шт. (керамическая плитка), неиспользовано 151 тыс. шт.
Полученные результаты занесем в таблицу:
| Ресурсы | Количество ресурсов | |||
| Наименование | в наличии | использованных | неиспользованных | |
| Арматура, т | 900 | 827 | 73 | |
| Пиломатериалы, м3 | 520 | 520 | - | |
| Цемент, т | 7 000 | 6 144 | 856 | |
| Керамическая плитка, тыс. шт. | 400 | 249 | 151 | |
| Трудозатраты, чел. дн. | 55 000 | 55 000 | -- | |
Вывод: Максимальное количество домов, которые можно отремонтировать, используя данные ресурсы – 498 шт. (кирпичные) и 406 шт. (панельные). При ремонте пиломатериалы и трудозатраты используются полностью, остальные ресурсы – с остатком.
Задание №3
Дата добавления: 2019-07-15; просмотров: 122; Мы поможем в написании вашей работы! |

Мы поможем в написании ваших работ!
