Визначення проблем банку. Напрямок майбутніх досліджень

Важливе місце в економіці відведена банкам, які регулюють грошовий оборот країни, акумулюють грошові ресурси і перерозподіляють їх. В процесі своєї активної діяльності банки стикаються з різного роду ризиками. Неефективне управляння ризиками в банківський діяльності може привести к банкрутству, а в силу його положення в економіці, і к цілому ряду банкрутств, зв’язаних з ним виробництв, банків та фізичних осіб.

Основним видом діяльності банка є кредитна, яка включає в середньому 50% доходності усіх активів, і як правило, висока доходність супроводжується підвищеним ризиком.

Приоритетні напрямки розвитку АКБ „Правекс-Банк”:

­ Споживче кредитування, кредитна картка „Росрочка”;

­ Пластикові картки – ЗК, часні, кредитні(універсальні, кредит під депозит, кредит під зарплату);

­ Рознічні послуги (обмін валют, „Правекс-Телеграф”, „обмін ветхої валюти”);

­ Продаж банківських металів, продаж іноземних монет;

­ Залогове кредитування;

­ Риночні послуги страхування( обов’язкове страхування граждансько-провової відповідальності власників транспортних средств)

З збільшенням об’ємів кредитування стає актуальними і задачі управляння кредитним ризиком банку. В зв’язку з цим розробка методів оцінки та механізму регулювання кредитного портфельного ризику забезпечує укріплення фінансового положення банку.

Недостатній рівень розвитку теоретичних та методологічних питань портфельного аналізу ризиків кредитних операцій в системі аналізу банківської діяльності обусловлює вибір теми роботи і свідчать о її актуальності.

Метою даної роботи є розробка економічно обоснованого механізму оцінки і регулюванні кредитним портфельним ризиком з метою задоволення інтересів банку, пов’язаних з мінімізацією ризику кредитного портфелю банка та підвищення доходності портфеля. Об’єктом даної роботи є кредитна діяльність банка, а також кредитний ризик, як основна частина кожної банківської операції. Відповідно до сучасних наукових підходів ця проблема може бути вирішена за допомогою математичних методів.

 

ЗАСТОСУВАННЯ ЕКОНОМІКО-МАТЕМАТИЧНИХ МЕТОДІВ

Методологічні підходи і проблеми щодо здійснення трансакцій

Якщо йдеться про оптимізацію траси платежів, то починати потрібно з транспортної задачі лінійного програмування, за допомогою якої загалом і здійснюється вибір найкращого шляху, в нашому випадку – фінансових платежів, при заданих умовах і обмеженнях.

 

Постановка транспортної задачі

Транспортна задача лінійного програмування формулюється так. Маємо m пунктів відправлення або банківських рахунків А₁, А₂,..,Аm, у яких знаходяться фінансові запаси відповідно а₁, а₂,..,а_m припустімо, євро. Крім того, є n пунктів призначення – банків кореспондентів В₁, В₂,...,Вn, в яких існують кореспондентські рахунки для отримання b₁, b₂,...,b_n грошових одиниць. Передбачається, що сума всіх переказів дорівнює сумі на таких рахунках, тобто

 

. (2.1)

 

Позначимо с_ij вартість переказу суми від кожного пункту відправлення, тобто нашого банку Аi до кожного пункту призначення Вj. Матриця вартостей С має вигляд

 

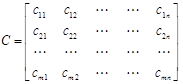. (2.2)

 

Потрібно скласти такий план переказів, при якому всі заявки були б виконані й загальна вартість усіх переказів була мінімальною. Таким чином, у якості критерію обрана вартість перевезення вантажу. Критеріями в транспортній задачі можуть бути такі показники: відстань, час, потужність та ін. Транспортна задача, в якій виконується умова, називається закритою. Задача, у якій ця умова не виконується, називається відкритою.

Ми будемо розглядати саме такий випадок, бо 95% усіх крупних банківських переказів здійснюються строго з одного рахунку на інший.

Математичне формулювання транспортної задачі може бути подано у такому вигляді: нехай x_ij – об’єм переказу, що відправляється з i-го пункту відправлення Аi в j-й пункт призначення Вj ( ), x_ij ³ 0. Змінні x_ij повинні задовольняти нерівностям (2.3. – 2.9.).

Будь-яку сукупність значень x_ij ( ) називають планом переказів. План, що задовольняє умовам (2.3) - (2.9), називають припустимим. Ранг системи (2.3) - (2.8) дорівнює r = m + n - 1, тоді в ній (m + n - 1) базисних та (m - 1)(n - 1) вільних змінних. Тому план, у якому відмінно від нуля не більш m + n - 1 змінних, а інші рівні нулю, називають опорним.

Оптимальний план - це такий план, що серед усіх припустимих має найменшу вартість перевезень. Пошук оптимального плану виконується за допомогою транспортної таблиці 2.1.

Вартість переказу поміщають у правому верхньому куті клітин таблиці. Клітини таблиці, у яких будемо записувати відмінні від нуля перевезення 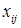 , називаються базисними. Таких клітин не більш ніж m+n - 1. Порожні клітини називаються вільними, їх не менше (m - 1)(n - 1).

 

 (2.3)

 (2.4)

 (2.5)

 (2.6)

 (2.7)

 (2.8)

. (2.9)

 

Таблиця 2.1 – Транспортна таблиця

 

Усі подальші дії по вирішенню транспортної задачі будуть зводиться до перетворення транспортної табл. 2.1, тобто до двох етапів:

а) відшукування першого розв'язання методом „північно-західного кута”;

б) пошуку оптимального розв'язання задачі за допомогою методу потенціалів.

Проте перед нами стоїть завдання залучити до математичної моделі такі обмеження, які неможливо задати в рамках транспортної задача, тому доцільним є використання іншого методу оптимізації – методу Ньютона.

Метод Ньютона

Якщо виходити з того, що необхідним етапом знаходження рішення задачі:

 

 (2.10)

 

 де f: R^m  R, є етап знаходження стаціонарних точок, тобто точок, задовольняючих рівнянню:

 

 (2.11)

 

(позначення F для f  ми зберігатимемо), тож можна спробувати вирішувати рівняння (2.11) відомим методом Ньютона рішення нелінійних рівнянь:

 

xⁿ⁺¹ = xⁿ  [F (xⁿ)]^1F(xⁿ). (2.12)

 

Для задачі (2.10) цей метод називається методом Ньютона безумовній оптимізації і задається формулою:

 

xⁿ⁺¹ = xⁿ  [f (xⁿ)]^1f (xⁿ).(2.13)

 

Формулу (2.12) можна вивести, виходячи з таких міркувань. Припустімо, що xⁿ — деяке наближене рішення рівняння (2.11). Тоді якщо замінити функцію F в рівнянні (2.11) її лінійним наближенням:

 

Стосовно задачі (2.10) ці міркування виглядають так. Нехай так само, у нас вже є деяке наближене рішення xn задачі (2.10). Замінимо в ній функцію f її наближенням другого порядку:

 

 

і як наступне наближення візьмемо рішення задачі:

 

 (2.15)

 

Та на початку для подальшого використання виведених формул, необхідно довести деякі твердження - якщо f (xⁿ) > 0, то рішення задачі (2.15) задається формулою (2.13).

 

Рисунок 2.1 - Геометрична інтерпретація формул (2.12) і (2.13) відповідно

 

Метод Ньютона відноситься до методів другого порядку, оскільки дляобчислення кожної ітерації потрібне знання другої похідної функції f. По тих же міркуваннях градієнтний метод відносять до методів першого порядку. Підкреслимо, що тут йдеться не про порядок збіжності методу, а про порядок використовуються методом похідних функції, що мінімізується.

 

---

Дата добавления: 2019-07-15; просмотров: 179; Мы поможем в написании вашей работы!

Поделиться с друзьями:

---

---

Мы поможем в написании ваших работ!