ОПИСАНИЕ ПРОГРАММНОГО ОБЕСПЕЧЕНИЯ

САМАРСКИЙ ГОСУДАРСТВЕННЫЙ АЭРОКОСМИЧЕСКИЙ УНИВЕРСИТЕТ имени академика С.П. КОРОЛЕВА

ИССЛЕДОВАНИЕ АЛГОРИТМОВ ОЦЕНКИ ПАРАМЕТРОВ БИОЛОГИЧЕСКИХ СИГНАЛОВ

Самара 2000

МИНИСТЕРСТВО ОБРАЗОВАНИЯ РОССИЙСКОЙ ФЕДЕРАЦИИ

САМАРСКИЙ ГОСУДАРСТВЕННЫЙ АЭРОКОСМИЧЕСКИЙ УНИВЕРСИТЕТ имени академика С.П. КОРОЛЕВА

ИССЛЕДОВАНИЕ АЛГОРИТМОВ ОЦЕНКИ ПАРАМЕТРОВ БИОЛОГИЧЕСКИХ СИГНАЛОВ

Методические указания

Самара 2000

Составитель В.Н. Конюхов

УДК 615.47

Исследование алгоритмов оценки параметров биологических сигналов: Метод. указания/ Самар. гос. аэрокосм. ун-т. Сост. В.Н. Конюхов. Самара, 2000. 17 с.

Изложены основные теоретические сведения об оптимальных методах оценки параметров сигнала, требованиях, предъявляемых к точечным оценкам, рассмотрены байесовские оценки при различных функциях потерь, свойства оценок максимального правдоподобия. Приведены описание программного обеспечения, реализующего алгоритмы оценки временного положения R-зубца электрокардиосигнала, и порядок выполнения работы.

Рекомендуются студентам специальности 190500. Подготовлены на кафедре радиотехники.

Печатаются по решению редакционно-издательского совета Самарского государственного аэрокосмического университета имени академика С.П. Королева.

Рецензенты: Л.М. Логвинов, В.М. Гречишников

СОДЕРЖАНИЕ

1. Краткие теоретические сведения

1.1. Общие положения

1.2. Постановка задачи оценки

1.3. Свойства оценок параметров сигнала

1.4. Методы оценки параметров

1.4.1. Байесовские оценки

1.4.2. Байесовские оценки для различных функций потерь

1.4.3. Оценка по максимуму функции правдоподобия

1.4.4. Оценка максимального правдоподобия амплитуды

детерминированного сигнала

1.4.5. Квазиоптимальные оценки параметров сигнала

2. Описание программного обеспечения

3. Описание исходных данных

4. Порядок выполнения работы

5. Содержание отчета

Контрольные вопросы

Список рекомендуемой литературы

Цель работы: изучение принципов построения оптимальных алгоритмов оценки параметров сигналов, сравнительных характеристик оптимальных и квазиоптимальных алгоритмов оценки для различных аддитивных смесей полезного сигнала и помех.

КРАТКИЕ ТЕОРЕТИЧЕСКИЕ СВЕДЕНИЯ

1.1. Общие положения

Задача оценки параметров биологических сигналов занимает одно из центральных мест во многих процедурах обработки данных в системах медико-биологического назначения. Качество оценки параметров биологических сигналов оказывает значительное влияние на достоверность и точность диагностики и, как следствие, на эффективность процесса лечения в целом. Например, постановка диагноза ишемической болезни сердца может проводиться по значению смещения ST- сегмента электрокардиосигнала (ЭКС) относительно нулевой линии. Помехи, присутствующие при регистрации ЭКС, изменяют это значение. В связи с этим возникает задача выбора таких алгоритмов обработки сигнала на фоне помех, которые обеспечивали бы наилучшую, по определенному критерию, оценку смещения ST- сегмента, снижающую вероятность неверной постановки диагноза.

Оценки параметров биологических сигналов, помимо использования в диагностических целях, применяются также для обеспечения нормальной работы отдельных функциональных узлов диагностических систем. Так, известно, что многие биологические сигналы изменяют свои амплитудные значения в широких пределах. Для согласования динамического диапазона биологических сигналов с динамическим диапазоном электронных устройств используются системы автоматической регулировки усиления, которые поддерживают уровень выходного сигнала в заданных пределах при изменениях входного сигнала. Информационным сигналом, по которому производится регулирование, в данном случае является амплитуда входного сигнала. Следовательно, необходима оценка амплитуды входного сигнала.

Кроме оценки параметров сигналов в диагностических системах медико-биологического назначения часто в качестве информационных управляющих параметров используются оценки параметров помех. Это делается для того, чтобы достоверность и точность получаемых диагностических показателей находилась в заданных пределах. Например при регистрации ЭКС амплитуда помехи от силовой сети может стать настолько велика, что вероятность правильного обнаружения R-зубцов ЭКС окажется очень мала. В результате полученные диагностические заключения окажутся недостоверными. В этом случае по результатам оценки амплитуды помехи появляется возможность выдачи предупреждающих сообщений обслуживающему персоналу в случае превышения помехой определенного уровня.

1.2. Постановка задачи оценки

В общем виде задача оценки параметра сигнала может быть поставлена следующим образом. Пусть на конечном интервале времени принимается сигнал , представляющий собой детерминированную функцию от полезного сигнала и помехи :

, (1)

где - параметры, от которых зависит сигнал. Требуется оптимальным образом, в соответствии с выбранным критерием, определить значение -го параметра сигнала . Если сигнал зависит от нескольких параметров, то аналогично может быть поставлена задача оценки двух или более параметров.

Результатом решения задачи оценки являются структурные схемы устройств оценки параметров и предельные точности измерения параметров сигнала.

Неизвестные параметры сигнала могут быть постоянными величинами, случайными величинами и случайными процессами. Различие между ними заключается в том, что

-постоянные параметры сигнала сохраняют свое значение в различных опытах; -случайные величины не изменяют своего значения в данном наблюдении, но могут принимать различные значения в различных наблюдениях;

-случайные процессы изменяются во времени при конкретном наблюдении.

Далее будем рассматривать алгоритмы оценки параметров сигнала , представляющих собой случайные величины.

Выше отмечалось, что построение алгоритма оценки опирается на выбранный критерий оптимальности. Для выбора в каждом конкретном случае критерия оптимальности необходимо определить, какие именно характеристики оценки параметра оказывают наибольшее влияние на конечный результат работы всей системы.

1.3. Свойства оценок параметров сигнала

Различают два вида оценок: интервальные (доверительные) и точечные. При интервальной оценке необходимо указать интервал, в котором с вероятностью не меньше заданной содержится истинное значение неизвестного параметра. Эта заданная вероятность называется коэффициентом доверия, а указанный интервал возможных значений - доверительным интервалом.

При точечной оценке неизвестному параметру сигнала приписывается одно значение из интервала возможных. Применительно к оценке параметров сигналов точечные оценки находят наибольшее применение.

Точечная оценка параметра из-за наличия шума является случайной величиной, изменяющейся от реализации к реализации, и наиболее полно характеризуется условной плотностью вероятности . На практике нахождение условной плотности вероятности часто затруднительно. Потому полагают, что близка к симметричной и унимодальна. В этом случае в качестве характеристик оценки вводят понятия смещения и дисперсии оценки.

Разность называется смещением или систематической ошибкой оценки. Оценка параметра называется несмещенной, если выполняется условие , где - математическое ожидание.

Дисперсия оценки определяется по формуле

. (2)

Оценка, имеющая наименьшую дисперсию, называется эффективной.

Минимально возможную дисперсию оценки параметра можно определить, воспользовавшись неравенством Рао-Крамера. Пусть необходимо оценить параметр сигнала по дискретной выборке :

, (3)

где - помеха. Тогда неравенство Рао-Крамера примет вид

, (4)

где - совместная плотность вероятности выборочных значений.

Существует несколько подходов к желательным свойствам точечной оценки.

1. Естественно пытаться построить такую оценку, чтобы условная плотность вероятности как можно теснее группировалась около истинного значения .

2. Желательно, чтобы при увеличении времени наблюдения или в отсутствии помех оценка совпадала с истинным значением оцениваемого параметра. В этом случае говорят, что оценка состоятельна.

3. Оценка должна быть несмещенной или асимптотически несмещенной. Асимптотическая несмещенность означает отсутствие смещения при или отношении сигнал/шум, стремящемся к бесконечности.

4. Оценка должна иметь минимальное значение дисперсии при нулевом или постоянном значении (эффективная оценка).

5. Оценка должна обладать свойствами достаточной статистики. Статистика называется достаточной, если все суждения об оцениваемом параметре могут быть вынесены без дополнительного обращения к реализации. Так, апостериорная плотность вероятности всегда является достаточной статистикой.

Критерий построения оценки определяется поставленной задачей. Например, выбор между смещенной оценкой с меньшей дисперсией и несмещенной с большей дисперсией зависит от того, для каких целей ищется оценка.

В зависимости от выбранного критерия и априорных сведений предложены различные методы оценки параметров сигнала.

1.4. Методы оценки параметров

1.4.1. Байесовские оценки

При любом выборе правила оценивания неизбежны ошибки из-за случайного характера наблюдаемой реализации. Вероятность появления ошибок различной величины зависит от выбранного правила оценивания. Последствия проявления ошибок в общем случае различны для каждой конкретной задачи. Чтобы учесть эти последствия вводится функция потерь. Функция потерь каждой комбинации и ставит в соответствие определенную, обычно неотрицательную, величину . Это означает, что каждой ошибке в зависимости от ее последствий приписывается определенный вес.

Наиболее часто на практике используются следующие функции потерь.

1. Простая функция потерь (рис.1), определяемая как

, (5)

где - дельта-функция Дирака.

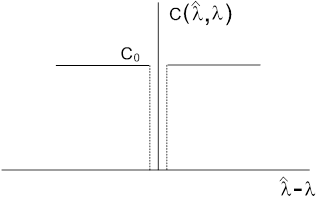
Рис. 1. Простая функция потерь

2. Квадратичная функция потерь (рис.2)

. (6)

Рис. 2. Квадратичная функция потерь

3. Линейная по модулю функция потерь (рис.3)

. (7)

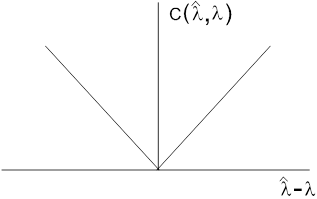
Рис. 3. Линейная по модулю функция потерь

4. Прямоугольная функция потерь (рис.4.), определяемая как

(8)

Рис. 4. Прямоугольная функция потерь

В общем случае функция потерь может быть несимметричной, например в ситуациях, когда отрицательные ошибки менее предпочтительны, чем положительные.

Так как и оценка , и оцениваемый параметр являются случайными величинами, то при любом выборе алгоритма получения оценки потери будут случайной величиной. В этом случае для того, чтобы сравнить между собой различные алгоритмы, вводят среднее значение потерь, называемое риском. При этом различают условный и безусловный риски. Условный риск определяется как

. (9)

Очевидно, что наиболее предпочтительными будут те оценки, для которых условный риск минимален. Однако при различных значениях параметра условный риск будет различным и, следовательно, будут различными предпочтительные правила оценки.

В том случае, если известна априорная плотность вероятности распределения параметра - , то наилучший алгоритм оценки необходимо искать исходя из минимума безусловного среднего риска:

, (10)

где - плотность вероятности выборки наблюдаемых данных.

Оценку, обеспечивающую минимум безусловного байесовского риска, называют байесовской оценкой, а минимальное значение безусловного среднего риска- байесовским риском.

Безусловный средний риск может быть вычислен для любого правила оценки. При этом всегда верно соотношение

, (11)

где - байесовский риск.

Вычисляя средний риск, можно судить, насколько одна оценка лучше другой и насколько какая-либо из оценок близка к оптимальной байесовской оценке.

1.4.2. Байесовские оценки для различных функций потерь

Рассмотрим байесовские оценки для линейной по модулю и прямоугольной функций потерь.

Учитывая, что в выражении (10) плотность вероятности 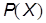является неотрицательной величиной, то минимизация выражения (10) сводится к минимизации апостериорного риска:

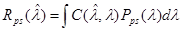. (12)

Тогда для линейной по модулю функции потерь выражение для апостериорного риска примет вид

(13)

Выражение (13) можно переписать в виде

. (14)

Находя производную по и приравнивая ее к нулю, получим

, (15)

что эквивалентно соотношению

. (16)

Отсюда следует, что минимальное значение апостериорного риска обеспечивается, если оценка параметра делит апостериорное распределение на две равные части, т.е. является медианой.

Для квадратичной функции потерь выражение апостериорного риска примет вид

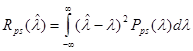. (17)

Дифференцируя по и приравнивая к нулю, получим

. (18).

Следовательно, оценка параметра, минимизирующая апостериорный риск, определится как

(19)

и будет являться математическим ожиданием апостериорного распределения параметра .

1.4.3. Оценка по максимуму функции правдоподобия

Для некоторых практических случаев априорное распределение параметра может быть неизвестно. В такой ситуации байесовский подход неприменим. В этом случае наиболее часто используют минимаксные оценки и оценки максимального правдоподобия (ОМП).

Суть минимаксного решения заключается в нахождении алгоритма , который минимизирует условный риск (9) для самого неблагоприятного случая:

. (20)

На практике отыскание минимаксного решения вызывает значительные трудности.

Другой наиболее частой оценкой при неизвестном априорном распределении параметра является ОМП. В этом случае оценкой параметра является такое число , при котором функция правдоподобия имеет максимальное значение:

. (21)

ОМП имеет ряд преимуществ по сравнению с другими, а именно:

n ОМП для широкого класса априорных распределений оцениваемого параметра близка к оценке по максимуму апостериорной вероятности, т.е. является байесовской при простой функции потерь;

n ОМП не зависит от взаимно однозначного безынерционного по оцениваемому параметру преобразования входного сигнала;

n при обработке сигнала на фоне нормального шума алгоритм ОМП не зависит от мощности помехи.

Устройство для получения ОМП параметра можно реализовать, например, следующим образом (рис.5).

Рис.5. Структурная схема устройства для получения ОМП

Здесь РУ- решающее устройство, которое выбирает максимальное значение среди m каналов. Число каналов m определяет разрешающую способность оценки параметра . Данную схему можно легко распространить на любое число оцениваемых параметров и т.д.

1.4.4. Оценка максимального правдоподобия амплитуды детерминированного сигнала

В качестве примера рассмотрим ОМП амплитуды детерминированного сигнала. Пусть обрабатываемый сигнал имеет вид

, (22)

где 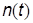- белый гауссовский шум с нулевым средним, а можно представить как

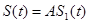. (23)

В свою очередь, - амплитуда сигнала.

Считаем, что все параметры сигнала , кроме амплитуды , известны. Тогда функционал правдоподобия примет вид

. (24)

Отсюда уравнение правдоподобия запишется как

(25)

и ОМП амплитуды детерминированного импульса определится следующим образом:

. (26)

В выражении (26) нижний интеграл представляет собой энергию сигнала. Следовательно, для того чтобы найти ОМП детерминированного сигнала, необходимо с помощью согласованного фильтра или коррелятора сформировать величину и разделить ее на энергию сигнала .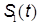

1.4.5. Квазиоптимальные оценки параметров сигнала

Из рассмотренного выше видно, что для получения оптимальных оценок необходимо иметь точную информацию о характере полезного сигнала и помех. На практике обычно такой полноты описания достигнуть не удается. Более того, часто при оценивании параметров физиологических сигналов как сами сигналы, так и помехи имеют нестационарный характер, изменяясь как во времени, так и от пациента к пациенту. В этом случае алгоритм оценки, оптимальный для одной выбранной модели смеси сигнала и помехи, становится неоптимальным при изменении параметров модели и ошибка оценки может стать существенной.

Кроме того, практическая реализация оптимальных алгоритмов оценки требует значительных аппаратных и (или) вычислительных затрат. Поэтому представляют интерес неоптимальные алгоритмы оценки параметров, которые позволяют значительно упростить реализацию устройства оценки при сохранении ошибки в заданных пределах.

Квазиоптимальные алгоритмы могут быть использованы в любом сечении устройства оценки параметров. Например, в качестве решающего устройства может использоваться пороговая схема, а за оценку неизвестного параметра принимается либо значение первого превышения 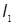порога функцией правдоподобия , либо среднее значение между двумя точками пересечения порогового уровня и (рис.6).

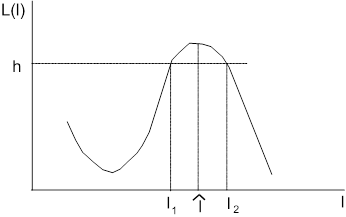
Рис. 6. Пример формирования квазиоптимальной оценки

ОПИСАНИЕ ПРОГРАММНОГО ОБЕСПЕЧЕНИЯ

Программное обеспечение представляет собой набор утилит, объединенных общим интерфейсом пользователя, и позволяет реализовать различные методы оценки длительности кардиоинтервалов (КИ) по исходному ЭКС. Кардиоинтервалом называют временной интервал между двумя соседними R-зубцами ЭКС. Внешний вид интерфейса приведен на рис 7.

Рис. 7. Внешний вид интерфейса

В папке меню «Файл» реализована функция открытия файла данных, в папке «Обработка»- функции формирования смеси сигнал+шум, получения квазиоптимальной оценки, оценки максимального правдоподобия, байесовской оценки длительности КИ при квадратичной функции потерь. Также в папке меню «Обработка» предусмотрена функция сохранения полученных результатов.

Формирование необходимой аддитивной смеси сигнала и помехи осуществляется путем выбора параметров в секциях «Тип помехи» и «Амплитуда помехи». Амплитуда помехи задается в единицах младшего разряда. Так, если АЦП имеет 8 разрядов, то максимальное число, которое соответствует данной разрядности, равно «255». Следовательно, амплитуда помехи «50» соответствует 6 разрядам.

Суть данной работы заключается в следующем. Известно, что длительности КИ не являются постоянной величиной, а меняются в каждом сердечном цикле. Изменения длительности КИ носят случайный характер. Массив КИ, полученный за определенный промежуток времени, можно охарактеризовать набором статистических характеристик (математическим ожиданием, дисперсией, среднеквадратическим отклонением и т.д.). В свою очередь, различными исследованиями показано, что даже такие простые характеристики массива КИ могут быть использованы как диагностические показатели для оценки тяжести тех или иных заболеваний. Так, например, при развитии диабетической полинейропатии уменьшается дисперсия временного ряда КИ, что позволяет оценить стадию заболевания по значениям дисперсии.

С другой стороны, оценка длительности КИ также является случайной величиной, обладающей определенной дисперсией. Если длительность КИ и оценка этой длительности являются независимыми случайными величинами, то результирующая дисперсия полученного массива КИ будет равна сумме дисперсии массива КИ, обусловленной физиологическими причинами, и дисперсии оценки. Чем больше дисперсия оценки длительности КИ, тем менее достоверно значение диагностического показателя. Следовательно, для систем, анализирующих вариабельность ритма сердца, необходимы алгоритмы, минимизирующие дисперсию оценки длительности КИ.

ОПИСАНИЕ ИСХОДНЫХ ДАННЫХ

Для исследования заданы три фрагмента записи электрокардиосигнала (ЭКС). Разные фрагменты ЭКС зарегистрированы у различных людей. Запись проводилась в специальной экранированной камере посредством прецизионного усилителя и вводилась в ПЭВМ с помощью 8 разрядного АЦП с динамическим диапазоном -5 - +5 В. Частота дискретизации для ЭКС составляет 1000 Гц. Имена файлов данных ЭКС-ecg1.dat, ecg2.dat, ecg3.dat.

ПОРЯДОК ВЫПОЛНЕНИЯ РАБОТЫ

1. С помощью папки меню «Файл» открыть файл данных ecg1. В правом верхнем углу экрана должно появиться имя открытого файла.

2. Получить оценки длительностей КИ тремя методами: пороговым методом, методом максимального правдоподобия, байесовским методом. Вычислить дисперсию массива КИ в каждом случае.

3. Повторить п.2 для смеси сигнала ecg1 и белого шума для трех амплитуд помехи. Оценить для каждой смеси сигнал+шум отношение сигнал/шум.

4. Повторить п.2 для смеси сигнала ecg1 и гармонической помехи для трех амплитуд помехи. Оценить для каждой смеси сигнал+шум отношение сигнал/шум.

5. Повторить пункты 1-4 для файлов ecg2 и ecg3.

Примечание. Оценки длительностей КИ могут быть сохранены в виде файла для автоматизированного расчета дисперсии с помощью команды меню «Сохранить полученные результаты оценок». Сохранение осуществляется в формате слова, где нечетный прочитанный байт из файла представляет собой младший байт оценки длительности КИ, а четный- старший.

СОДЕРЖАНИЕ ОТЧЕТА

Отчет должен содержать:

n наименование и цель работы;

n графики зависимости дисперсии оценки от отношения сигнал/шум для трех файлов данных и трех методов оценки. Для каждого файла данных и типа помехи строится один график для трех методов;

n Выводы.

Все рисунки и графики должны иметь надписи, поясняющие, для каких данных и при каких условиях они получены, указание, какому именно методу оценки принадлежит та или иная зависимость, а также численные значения и единицы измерения на осях.

КОНТРОЛЬНЫЕ ВОПРОСЫ

1. Приведите примеры решения задачи оценки в процедурах обработки медико-биологических сигналов.

2. Приведите в общем виде постановку задачи оценки параметров сигналов. Что является результатом решения задачи оценки?

3. Какими могут быть параметры сигнала, подлежащие оценке? В чем заключается различие между ними?

4. Какие виды оценок существуют? В чем различие между ними?

5. Что является наиболее полной характеристикой оценки?

6. Каким образом и при каких ограничениях определяются понятия смещения и дисперсии оценки?

7. Что такое эффективная оценка?

8. Приведите неравенство Рао-Крамера. Что можно определить с помощью неравенства Рао-Крамера?

9. Перечислите желательные свойства точечной оценки параметра сигнала.

10. Что такое функция потерь? В чем ее физический смысл?

11. Как определяются простая, квадратичная, линейная по модулю и прямоугольная функции потерь?

12. Приведите выражения для условного и безусловного риска. Что характеризует условный и безусловный риски?

13. Что такое байесовский риск и байесовская оценка?

14. Выведите выражение для байесовской оценки для линейной по модулю функции потерь. Что в этом случае представляет собой байесовская оценка?

15. Выведите выражение для байесовской оценки для квадратичной функции потерь. Что в этом случае представляет собой байесовская оценка?

16. В каких случаях байесовский подход неприменим? Какие оценки используют в этой ситуации?

17. В чем суть минимаксной оценки?

18. Каким образом определяется оценка максимального правдоподобия?

19. Какие преимущества имеет оценка максимального правдоподобия?

20. Приведите структурную схему устройства для получения оценки максимального правдоподобия параметра сигнала?

21. Выведите выражение для оценки максимального правдоподобия амплитуды детерминированного сигнала.

22. В чем причина использования казиоптимальных оценок сигнала? Приведите примеры квазиоптимальных оценок.

Дата добавления: 2019-02-22; просмотров: 108; Мы поможем в написании вашей работы!

Поделиться с друзьями:

Мы поможем в написании ваших работ!