МАТЕМАТИЧЕСКАЯ ЛОГИКА, БУЛЕВЫ ФУНКЦИИ
Приложение 2
Задания на защиту контрольной работы
Примечание: номер задачи со звездочкой указывает на ее повышенную сложность.
Теория множеств
1. Условимся множество, содержащее элементы 
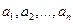 , записывать в виде A = {
, записывать в виде A = { 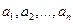 }.
}.
Дайте ответы на вопросы и обоснуйте их:
а) равны ли множества {{1, 2}} и {1, 2}? 
б) равны ли множества {{1, 2, 3}, {2, 3}} и {1, 2, 3}? 
2. Напомним, что если между элементами двух множеств можно установить взаимно однозначное соответствие, то говорят, что эти множества равномощны.
Дайте ответы на вопросы и обоснуйте их:
а) множество всех натуральных чисел равномощно множеству всех четных положительных чисел?
б) множество всех четных положительных чисел равномощно множеству всех нечетных положительных чисел?
3. Для множеств А, В, С Í U из задачи 4 определить содержательный смысл следующих множеств:
а) А Ç (В \ С); б) (А Ç В) \ С; в) В \ 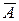 ;
;
г) (А Ç В) È С; д) А Ç (В È С).
4. Пусть U = {a, b, c, d}, X = {a, c}, Y = {a, b, d}, Z = {b, c}. Найти множества:
а) X Ç 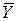 ; б) (X Ç Z) È
; б) (X Ç Z) È 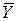 ; в) X È (Y Ç Z);
; в) X È (Y Ç Z);
г) (X È Y)Ç (X È Z); д) X È Y; е) 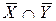 ;
;
ж) 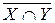 ; з) (X È Y) È Z; и) X È (Y È Z);
; з) (X È Y) È Z; и) X È (Y È Z);
к) X \ 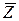 ; л) (X \ Z)È (Y \ Z).
; л) (X \ Z)È (Y \ Z).
5. Пусть U = {1, 2, 3, 4, 5, 6}; A = {1, 2, 3}; B = {1, 3, 5, 6}; C = {4, 5, 6}. Найти множества:
|
|
|
а) A \ C; б) B \ C; с) C \ B; г) A \ B; д) 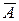 È B;
È B;
е) B Ç 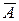 ; ж) А Ç С; з) (C È A) \ (C Ç A).
; ж) А Ç С; з) (C È A) \ (C Ç A).
6. Даны два произвольных множества А и В такие, что А Ç В = Æ. Что представляют собой множества A \ B и В \ А?
7. Даны два произвольных множества C и D такие, что C Ç 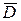 = Æ. Что представляют собой множества C Ç D, C È D ?
= Æ. Что представляют собой множества C Ç D, C È D ?
8. Представить множество А È (B Ç 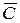 ) диаграммой Венна.
) диаграммой Венна.
9. Проиллюстрировать на конкретных множествах и с помощью диаграммы Венна справедливость соотношения
А Ç (B È C) = (А Ç B) È(А Ç C).
10. Построить диаграммы Венна, иллюстрирующие множества а) – л) из задачи 6.
11. Проиллюстрировать на конкретных множествах и с помощью диаграмм Венна справедливость соотношений:
а) (А È B)Ç C = (А Ç C) È (B Ç C);
б) А È (B Ç C) = (А È B) Ç (А È C);
в) (А Ç B)È C = (А È C) Ç (B È C).
12. Пусть А, В, С Í U . Проиллюстрировать на примере конкретных множествах и с помощью диаграмм Венна справедливость следующих соотношений:
а) А Ç (B Ç C) = (А Ç B) Ç C; б) А È (B È C) = (А È B) È C;
в) 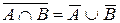 ; г)
; г) 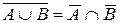 ;
;
д) А È (А Ç B) = А; е) А Ç (А È B) = А;
ж) (А Ç B) È(А Ç 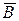 ) = А; з) А È (
) = А; з) А È ( 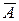 È B) = А È B .
È B) = А È B .
|
|
|
Отношения
1. Пусть X = {1, 2, 3}, Y = {a, b}. Построить декартовы произведения:
X ´ Y ; Y ´ X ; Y 3 ; X 2.
2. Пусть x, y – прямые на плоскости. Задано бинарное отношение r следующим образом r = {( x, y) | x пересекается с y}. Будем считать, что прямая x пересекается с прямой y, если они имеют по крайней мере одну общую точку. Обладает ли отношение r свойствами рефлексивности, симметричности, антисимметричности, транзитивности?
3. Пусть r = { ( x, y) | x не пересекается с y }, x, y – прямые на плоскости. Каковы свойства этого отношения?
4. Бинарному отношению R Í M ´ M, где M = {a1, a2, …, an}, соответствует квадратная матрица порядка n, в которой элемент равен
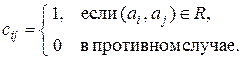

Пусть M = {1, 2, 3, 4, 5, 6}.
Составить матрицы отношений R1 , R2 , R3 Í M´M, если
а) R1 – « быть делителем »;
б) R2 – « иметь общий делитель, отличный от 1 »;
в) R3 – « иметь один и тот же остаток от деления на 3 ».
5. Для указанных ниже отношений, заданных на множестве точек действительной плоскости, привести примеры пар, для которых выполняются отношения, и пар, для которых не выполняются отношения:
а) R1 – « находиться на одинаковом расстоянии от начала координат »;
б) R2 – « находиться на разном расстоянии от начала координат »;
|
|
|
в) R3 – « находиться на одной и той же окружности с центром в начале координат »;
г) R4 – « быть симметричным относительно оси X ».
6. Множество всех подмножеств множества M обозначим через b(M). Составьте матрицы отношений, заданных на системе множеств b(M), где M = {a, b, c}:
а) R1 – « пересекаться с … » (иметь непустое пересечение);
б) R2 – « являться строгим включением ( Ì ) ».
7. Пусть M = b(А), А = {1, 2, 3, 4}. Найти все элементы (пары) отношения R на M, если R означает:
а) Ì ; б) Í ; в) « пересекаться с … »;
г) « быть дополнением к … ».
8. Пусть отношение R на M = {1, 2, 3, 4, 5, 6, 7, 8, 9}. Выписать все элементы R, если:
а) R = { (a, b): a, b Î M; (a + 1) – делитель (a + b) };
б) R = { (a, b): a, b Î M; a – делитель (a + b), a ¹ 1 }.
9. Какими признаками характеризуется матрица отношения R, если R соответственно:
1) рефлексивно; 2) антирефлексивно;
3) симметрично; 4) антисимметрично;
5) транзитивно?
10. Каковы свойства отношений, заданных на множестве натуральных чисел N: а) R1 – « быть не больше ( £ ) »; б) R2 – « быть делителем »;
в) R3 – « быть равным ».
11. Каковы свойства отношений, заданных на множестве людей:
а) R1 – « быть сыном »;
б) R2 – «жить в одном городе »;
в) R3 – « быть братом ».
|
|
|
12*. Рассмотрим отношение предшествования слов упорядоченного конечного алфавита A (обозначается как 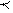 ), называемого лексикографическим упорядочением. Определим это отношение следующим образом. Пусть даны слова a1 = a11a12…a1n и a2 = a21a22…a2n , тогда a1
), называемого лексикографическим упорядочением. Определим это отношение следующим образом. Пусть даны слова a1 = a11a12…a1n и a2 = a21a22…a2n , тогда a1 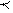 a2 тогда и только тогда, когда
a2 тогда и только тогда, когда
а) a1 = b ai g , a2 = b aj d и ai 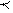 aj , где b, g, d – некоторые слова, возможно пустые, ai , aj – буквы, либо
aj , где b, g, d – некоторые слова, возможно пустые, ai , aj – буквы, либо
б) a2 = a1b, где b – непустое слово.
Является ли это отношение отношением строгого порядка (линейным)?
13. На множестве людей заданы следующие отношения:
а) быть не старше; б) быть моложе; в) быть прямым потомком.
Какие из этих отношений являются отношением строгого порядка, а какие – нестрогого порядка?
14. К каким типам отношений относятся отношения « £ » и « < » на множестве векторов длины n с целыми координатами, определяемые следующим образом:
а) (a1, a2, …, an) £ (b1, b2, …, bn) , если a1 £ b1 , …, an £ bn ;
б) (a1, a2, …, an) < (b1, b2, …, bn) , если (a1, a2, …, an) £ (b1, b2, …, bn) и хотя бы для одной координаты выполняется ai £ bi .
15. Пусть на множестве R действительных чисел задано бинарное отношение
r = { (x, y) | x 2 + x = y 2 + y } .
Докажите, что это есть отношение эквивалентности.
16*. На множестве целых чисел Z задано отношение сравнимости по модулю: x º y ( mod n ), n – натуральное число, если и только если (x – y ) делится без остатка на n . Докажите, что это есть отношение эквивалентности.
17*. На множестве N ´ N , где N – множество натуральных чисел, определено отношение r следующим образом:
r = { < x, y > , < u, v > | x v = yu } .
Докажите, что это есть отношение эквивалентности.
МАТЕМАТИЧЕСКАЯ ЛОГИКА, БУЛЕВЫ ФУНКЦИИ
1. С применением таблиц истинности для логических операций доказать, что следующие логические формулы являются тавтологиями (тождественно истиными):
а). 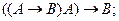 б).
б). 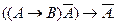
2. Вычислить значения трех представленных булевых функций на наборах значений (0,1,0), (1,0,0), (0,1,1),(1,0,1):
а). 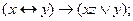 б).
б). 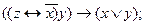 в).
в). 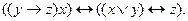
3. С применением таблиц истинности для логических операций доказать, что следующие логические формулы являются тавтологиями (тождественно истинными):
а). 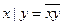 – штрих Шеффера; б).
– штрих Шеффера; б). 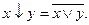 – стрелка Пирса.
– стрелка Пирса.
4. Логическую функцию трех переменных
f (x, y, z) = 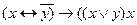 представить в виде СДНФ и СКНФ.
представить в виде СДНФ и СКНФ.
5. Доказать справедливость представления основных логических операций следующими формулами:
1). 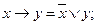 2).
2). 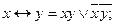 3).
3). 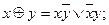 – сумма по модулю 2
– сумма по модулю 2
4). 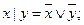 – штрих Шеффера; 5).
– штрих Шеффера; 5). 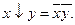 – стрелка Пирса.
– стрелка Пирса.
6. Подсчитать число различных булевых функций от двух, трех, четырех и пяти переменных соответственно.
7. Набор булевых функций { 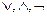 } есть функционально полная система (базис). Исходя из этого доказать, что следующие наборы функций также являются функционально полными системами:
} есть функционально полная система (базис). Исходя из этого доказать, что следующие наборы функций также являются функционально полными системами:
а). { 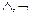 } ; б) {
} ; б) { 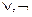 }; в). {
}; в). { 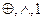 } – алгебра Жегалкина;
} – алгебра Жегалкина;
г). { 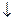 } – стрелка Пирса; д). {|} – штрих Шеффера.
} – стрелка Пирса; д). {|} – штрих Шеффера.
8. Построить СДНФ и СКНФ логической функции f (x, y, z), используя табличное представление функции, если она задана следующей логической формулой:
1). 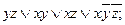 2).
2). 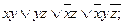 3).
3). 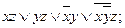
4). 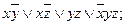 5).
5). 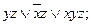 6).
6). 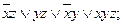
7). 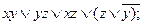 8).
8). 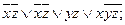 9).
9). 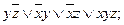
10). 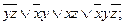 .
.
9. Упростить булевы формулы:
а). f (x, y, z) = 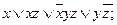
б). f (x, y, z) = 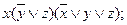 .
.
10. Построить логическую функцию от трех переменных, которая принимает значение «истина» тогда и только тогда, когда:
а) ровно одна переменная ложна;
б) ровно две переменные ложны.
11. Представить логическую формулу 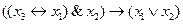 в базисах {&,
в базисах {&, 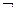 } и {
} и { 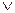 ,
, 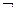 }.
}.
12. Пусть f (x, y, z) = x 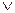 yz
yz 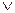
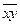 z. Требуется упростить эту формулу и получить ее СДНФ.
z. Требуется упростить эту формулу и получить ее СДНФ.
13. Привести формулу к КНФ: f (x, y, z) = x 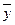
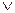
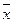 y
y 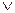
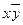 .
.
14. Пусть f (x, y, z) = x 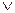 yz
yz 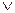
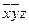 . Требуется упростить эту формулу и получить ее СКНФ.
. Требуется упростить эту формулу и получить ее СКНФ.
15. Привести следующие формулы к ДНФ:
1). 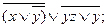 2).
2). 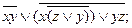 3).
3). 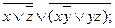
4). 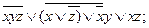 5).
5). 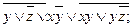 6).
6). 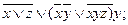
7). 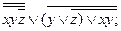 8).
8). 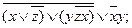 9).
9). 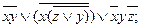
10). 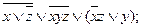
16. Пусть предикат P(x, y) описывает отношение «x любит y» на множестве людей. Привести все варианты квантификации обеих переменных. Дать словесную интерпретацию полученных высказываний.
17. Пусть предикат P(x, y) описывает отношение «x 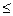 y» на множестве действительных чисел. Привести все варианты квантификации обеих переменных. Определить истинность полученных высказываний.
y» на множестве действительных чисел. Привести все варианты квантификации обеих переменных. Определить истинность полученных высказываний.
18*. Записать с использованием кванторов следующие математические утверждения:
1). По меньшей мере один объект обладает свойством Р.
2). Не более чем один объект обладает свойством Р.
3). Один и только один объект обладает свойством Р.
4).Уравнение ax = b имеет хотя бы один корень.
5). Уравнение ax = b имеет не более одного корня.
6). Уравнение ax = b имеет один и только один корень.
7). Множество М содержит по меньшей мере один элемент.
8). Множество М содержит не более одного элемента.
9). Множество М содержит ровно один элемент.
10). Уравнение f (x) =0 имеет не более двух корней.
19. Используя правила построения отрицания высказываний, начинающихся с кванторов общности и существования, сформулируйте отрицание следующих высказываний в утвердительной форме (т. е. так, чтобы они не начинались со слов «неверно, что…» или «не…»):
1). Из всякого положения есть выход.
2). В каждой стране найдется город, у всех жителей которого один и тот же цвет глаз.
3). В любой стране есть город с численностью населения более миллиона человек.
4). Существует страна, в которой нет ни одного города с миллионом жителей.
5). В любом городе есть районы, в которых дома имеют не более пяти этажей.
6). В любом городе есть школы, один из выпускников которой каждый год поступает в столичный вуз.
7). Существуют книги, в которых на каждой странице которой находится рисунок.
8). В каждой школе имеются учащиеся, выполнившие нормативы спортсмена 1 – 3 разрядов.
9). Все кошки имеют зеленый цвет глаз.
10). Все птицы имеют звонкие голоса.
Дата добавления: 2019-03-09; просмотров: 775; Мы поможем в написании вашей работы! |

Мы поможем в написании ваших работ!
