Тема 3 Принципы и технологии численного TOUGH2- моделирования (8 часов).
Численная реализация управляющих уравнений многофазной неизотермической геофильтрации. Вычислительные сетки. Модули состояния EOS .
Программное обеспечение (TOUGH2, PetraSim), модули состояния (EOS1, EOS2), генерация вычислительных сеток, задание начальных, граничных условий, материальные свойства и зонирование модели, технология выполнения моделирования (параметры выполнения и вывода результатов, анализ результатов моделирования). Интегро-конечно-разностный (ИКР) метод, уравнения массового и энергетического баланса, закон Дарси в конечно-разностном виде. Инвариантность TOUGH2-моделей по отношению к геометрии пространства и связанные с этим численные ограничения. Методы решения систем разностных уравнений, понятие сходимости в TOUGH2. Архитектура и основные модули программы TOUGH2. Модули состояния флюида (EOS), определение фазового состояния на численной модели.
Генерация полигональных и прямоугольных вычислительных сеток с учетом двойной пористости, негоризонтального залегания пластов и наличия разломов, моделирование ненарушенного состояния, задание на модели добычных и инжекционных скважин, 3D анализ результатов. Использование моделей нулевой размерности (состоящих из 1-го элемента).
Использование пре- и пост-процессоров, ГИС (Surfer-13, Grapher-8) для подготовки исходных данных и анализа результатов моделирования.
Запишем управляющие уравнения многофазной неизотермической геофильтрации (1.1 – 1.7) в конечно-разностном виде на дискретной вычислительной сетке изображенной на рисунке ниже:
|
|
|
Аккумулятивный член для компоненты К в (1.1):
(3.1)
Потоковые члены для компоненты К в (1.1):
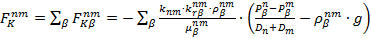(3.2)
Источники и стоки для компоненты К в (1.1):
(3.3)
Будем рассматривать процесс на дискретной последовательности времени (t1, t2, … tj, tj+1, ..). После чего уравнения сохранения (1.1) записываются для каждой компоненты К следующим образом:
(3.4)
Для численного решения системы из NEL*(NK+1) уравнений вводятся невязки (остатки) 
которые определяются для каждого элемента n и компонента К в указанном элементе:
(3.5)
Решение (3.5) находится для основных переменных модели {xi; i = 1, ..., NEL*(NК+1)} методом итераций Ньютона-Рафсона, где р – индекс итерации:
(3.6)
Для рассматриваемого нами случая система соответствующих алгебраических уравнений записывается следующим образом, где коэффициенты 
Якобианской матрицы определяются численным дифференцированием:
(3.7)
Успешное завершение итерационного процесса определяется условиями 
):
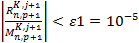(3.8)
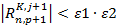(3.9)
Генерация вычислительных сеток:
PetraSimManual.pdf
Дата добавления: 2019-02-26; просмотров: 214; Мы поможем в написании вашей работы! |
Мы поможем в написании ваших работ!