Найти площадь трапеции по сторонам 4, 6,8,7.
ЭКЗАМЕНАЦИОННЫЙ билет № 15
Аксиоматический метод изложения математических теорий.
Аксиоматический метод – это способ построения научной теории, при котором в её основу кладутся некоторые исходные суждения — аксиомы, из которых все теоремы должны выводиться чисто логическим путём, посредством доказательств. Построение науки на основе аксиоматического метода обычно называется дедуктивным. Все понятия дедуктивной теории вводятся посредством определений, разъясняющих их через ранее введённые понятия.
Аксиоматический метод прошёл в своём историческом развитии 3 стадии:
Первая стадия связана с построением геометрии в Древней Греции. Основное сочинение этого периода — «Начала» Евклида, учения Пифагора, которому приписывается открытие аксиоматического метода, а затем Платон. В то время считалось, что в качестве аксиом должны выбираться суждения, истинность которых «самоочевидна», так что истинность теорем считалась гарантированностью логики.
Вторая стадия в истории аксиоматического метода связывается обычно с открытием Николаем Лобачевским, Яношем Больяй и Карлом Гауссом возможности построить непротиворечивым образом геометрию, исходя из систем аксиом, отличной от евклидовой. Это открытие разрушило убеждение в абсолютной истинности аксиом и основанных на них научных теорий.
Третья началась с эпохи деятельности Д. Гильберта, когда он выдвинул свою программу обоснования математики (1922). В этот период все выводы математической теории полностью формализованы, являются последовательностью формул, по которым из аксиом или ранее доказанных предложений выводятся другие предложения на основе списка правил. При этом ни аксиомам, ни теоремам не придается никакого конкретного смысла. Зато они обладают большой общностью.
|
|
|
Суть аксиоматического метода построения научной теории состоит в следующем: перечисляются основные (неопределяемые) понятия - все вновь возникающие понятия должны быть определены через основные понятия и понятия, определенные ранее.-- Далее формулируются аксиомы – предложения, принимаемые без доказательства. Доказывая какое-либо утверждение, опираются на некоторые предпосылки, которые считаются известными. Все остальные предложения должны являться логическим следствием аксиом или ранее доказанных утверждений.
Пример: Исходные понятия: точка, прямая, лежать на («точка лежит на прямой»).
Аксиомы: (A1) Через любые две точки проходит прямая. (A2) Любые две различные точки могут лежать не более чем одной прямой. (A3) На каждой прямой лежат по меньшей мере две точки. (A4) Существуют три точки, не лежающие на одной и той же прямой.
|
|
|
Формальная запись: 
Теоретико-групповой подход к изучению евклидовой геометрии
Во второй половине XIX века немецкий математик Феликс Клейн (1849-1925) определил геометрию как науку о свойствах фигур, не изменяющихся при всех преобразованиях некоторой группы. Свои геометрические идеи он изложил в знаменитой работе «Сравнительное обозрение новейших геометрических исследований» (1872). Он писал, что пусть даны некоторое S и группа преобразований G этого пространства. Тогда задача геометрии — изучить свойства фигур пространства S, инвариантные относительно группы G (т. е. такие свойства, которые сохраняются при любых преобразованиях из G).
Пусть дана группа преобразований G некоторого непустого множества М. Две фигуры F и F' называются G-эквивалентными, если в группе G найдётся такое преобразование f, что f(F)=F'.
Понятие G-эквивалентности является отношением эквивалентности на множестве всех подмножеств множества М. Например, если М - множество точек плоскости, а G – группа движений, то «G-эквивалентность» заменяется термином «равенство».
Пусть F – данная фигура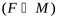 
. Те свойства фигуры F, которые сохраняются при любых преобразованиях из G, называют инвариантными свойствами фигуры F относительно группы G. Итак, в зависимости от группы , а так же видов фигур, на которые эта группа действует, возможно, множество геометрий.
|
|
|
Пример 1. Евклидова геометрия плоскости («школьная» геометрия плоскости) является геометрией группы подобия. Т. е. евклидова геометрия рассматривает свойства фигур, которые сохраняются при преобразовании подобия. Иногда о евклидовой геометрии говорят как о группе движений .
Пример 2. Аффинная геометрия плоскости – является геометрией группы аффинных преобразований плоскости.
В аффинной геометрии можно говорить о точках прямых, но так как расстояние при аффинном преобразовании может меняться, то, например, для аффинной геометрии:
1) Понятие равнобедренный, прямоугольный, равносторонний треугольник является идентичным – есть просто треугольник.
2) Нет окружностей, а есть просто эллипс.
3) Отсутствуют многие теоремы евклидовой геометрии, так нет теоремы Пифагора (она не выполняется), а теорема о делении медиан точкой их пересечения – выполняется.
Найти площадь трапеции по сторонам 4, 6,8,7.
Дата добавления: 2019-02-26; просмотров: 210; Мы поможем в написании вашей работы! |
Мы поможем в написании ваших работ!