Среднее геометрическое значение

Числовые характеристики распределений.

Для экспериментальных данных, полученных по выборке, можно вычислить ряд числовых характеристик (мер).

Центральная тенденция – то количественное (численное) значение признака, к которому тяготеет переменная величина. Поскольку понятие «тяготеет» несколько произвольно и с математической точки зрения не вполне корректно, имеет смысл рассмотреть различные меры центральной тенденции более подробно.

В психологических исследованиях в качестве мер центральной тенденции чаще всего используются мода, медиана и среднее арифметическое значение. Значительно реже используются такие меры как среднее геометрическое, среднее гармоническое, обратное среднее гармоническое значение и др.

Мода

Числовой характеристикой выборки, как правило, не требующей вычислений, является так называемая мода.

Мода — это такое числовое значение, которое встречается в выборке наиболее часто. Мода обозначается иногда как

Пример. В ряду значений (2, 6, 6, 8, 9, 9, 9, 10) модой является 9, потому что 9 встречается чаше любого другого числа. Мода представляет собой наиболее часто встречающееся значение (в данном примере это 9), а не частоту встречаемости этого значения (в данном примере равную 3).

Моду находят согласно следующим правилам:

1) В том случае, когда все значения в выборке встречаются одинаково часто, принято считать, что этот выборочный ряд не имеет моды.

Пример. 5, 5, 6, 6, 7, 7 — в этой выборке моды нет.

2) Когда два соседних (смежных) значения имеют одинаковую частоту и их частота больше частот любых других значений, мода вычисляется как среднее арифметическое этих двух значений.

Пример. В выборке 1, 2, 2, 2, 5, 5, 5, 6 частоты рядом расположенных значений 2 и 5 совпадают и равняются 3. Эта частота больше, чем частота других значений 1 и 6 (у которых она равна I)

Следовательно, модой этого ряда будет величина

В случае одной моды выборку называют мономодальной.

3)Если два несмежных (не соседних) значения в выборке
имеют равные частоты, которые больше частот любого
другого значения, то выделяют две моды.

Пример. В ряду 10, 11, 11, 11, 12, 13, 14, 14, 14, 17 модами являются значения 11 и 14.

В таком случае говорят, что выборка является бимодальной.

Могут существовать и так называемые мультимодальные (полимодальные) распределения, имеющие более двух вершин (мод).

4) Если мода оценивается по множеству сгруппированных
данных, то для нахождения моды необходимо определить
группу с наибольшей частотой признака. Эта группа называется модальной группой или модальным классом.

Мода не является достаточно строгой мерой центральной тенденции, поскольку она не учитывает характера распределения переменных, а значит может использоваться лишь в предварительных выводах и прогнозах. Кроме того, необходимо использовать моду только для больших объемов выборок, поскольку для малых она недостаточно информативна.

Медиана

Медиана (Md) – значение, которое делит упорядоченное множество данных (или ранжированный ряд) пополам так, что одна половина значений оказывается больше, а другая – меньше медианы. Медиана – среднее значение ранжированного ряда.

Если число значений нечетное, то медиана соответствует среднему члену ряда, если четное, то медиана есть среднее между двумя центральными значениями.

Мода и медиана не учитывают разброса данных, и переменные, лежащие в стороне от центра, не влияют на их величину.

Пример. Найдем медиану выборки: 9, 3, 5, 8, 4, 11, 13.

Сначала упорядочим выборку по величинам входящих в нее значений. Получим: 3, 4, 5, 8, 9, 11, 13. Поскольку в выборке семь элементов, четвертый по порядку элемент будет иметь значение большее, чем первые три, и меньшее, чем последние три. Таким образом, медианой будет четвертый элемент — 8.

Пример. Найдем медиану выборки 20, 9, 13, 1, 4, 11.

Упорядочим выборку. 1, 4, 9, 11, 13, 20. Поскольку здесь имеется четное число элементов, то существует две «середины» — 9 и 13. В этом случае медиана определяется как среднее арифметическое этих значений.

Среднее арифметическое значение

Среднее арифметическое значение,или просто среднее ( 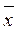), равно сумме переменных, деленной на их число.

Для несгруппированных переменных среднее арифметическое вычисляется по формуле:

Здесь величины 1, 2...,n называются индексами.

Для сгруппированных переменных можно воспользоваться другой формулой – среднее будет соответствовать сумме произведений средних значений каждого класса и частоты встречаемости значения признака в данном классе:

Среднее арифметическое может использоваться и для тех признаков, для которых не найден способ количественного измерения (шкала порядка). Для этого в качестве x_i используются ранговые числа, а среднее принято называть непараметрическим средним.

Взвешенное среднее арифметическое используется в тех случаях, когда разные составляющие имеют разный «удельный вес» в формировании общей совокупности:

или:

где n – объем выборки, N – число классов.

Пример. Средний балл аттестата учащихся выпускных классов одной из школ соответствует следующим значениям: 11-а – 4,2; 11-б – 4,0 и 11-в – 3,8. Численность этих классов составляет: 11-а – 25 человек, 11-б – 28 и 11-в – 32 человека. В данном случае средний балл аттестата по всем выпускным классам составит (4,2 × 25 + 4,0 × 28 + 3,8 × 32) : (25 + 28 + 32) = 3,98.

Среднее принято округлять с точностью до знака, следующего за последним знаком x_i (увеличение точности на порядок).

Следует подчеркнуть, что средние величины характеризуют выборку одним (средним) числом. Преимущество, или иначе, информативная значимость, средних величин заключается в их способности аккумулировать или уравновешивать все индивидуальные отклонения, в результате чего проявляется то наиболее устойчивое и типичное, что характеризует качественное своеобразие варьирующего объекта, позволяя отличить одну выборку от другой, а на этой основе, например, одно измеренное психологическое свойство от другого.

Однако среднее как статистический показатель не лишено недостатков Так, например, при определении среднего числа учеников, обучающихся в пятых классах данной школы, может быть получена величина равная 30,07 Конечно, с точки зрения статистика эти величины обычны, но для психологических задач они могут быть неприемлемы.

Кроме того, среднее оказывается достаточно чувствительным к очень маленьким или очень большим величинам, отличающимся от основных значении измеренных характеристик. Приведем пример из книги Дж Б Мангейма и Ричарда К. Рича «Политология. Методы исследования» М , 1997 г. «Пусть 9 человек имеют доход от 4500 до 5200 тыс долларов в месяц. Величина их среднего дохода равняется 4900 долларов. Если же к этой группе добавить человека, имеющего доход в 20000 тыс. долларов в месяц, то средняя всей группы сместится и окажется равной 6410 долларов, хотя никто из всей выборки (кроме одного человека) реально не получает такой суммы. Понятно, что аналогичное смещение, но в противоположную сторону можно получить и в том случае, если добавить в эту группу человека с очень маленьким годовым доходом».

Размах выборки

Разброс (размахом) выборки называют разность между максимальной и минимальной величинами данного конкретного вариационного ряда, т.е.

Среднее геометрическое значение

Среднее геометрическое значение (xg) используется для вычисления центральной тенденции, когда распределение значений переменной имеет выраженную положительную (правостороннюю) асимметрию.

Формула среднего геометрического:

Дата добавления: 2019-02-26; просмотров: 457; Мы поможем в написании вашей работы!

Поделиться с друзьями:

Мы поможем в написании ваших работ!