Осьтік екпіндік моменті. Екпіндік радиусы.
ДӘРІС ДИНАМИКА ДИНАМИКАҒА КІРІСПЕ. МАТЕРИАЛЫҚ НҮКТЕ ДИНАМИКАСЫ 11.1. Динамика мәселелері Динамикада материялық нүктелер мен материялық денелердің қозғалыстары оларды болдыратын физикалық себептермен (күштермен) тығыз байланысты қарастырылады. Денеге түсірілген күштер мен олардың әсерлерінен болатын қозғалыс арасындағы тәуелділікті зерттеу, сөйтіп қозғалыстың жалпы заңдылығын табу мәселелері қаралады. Динамиканың өзі екі бөлімге бөлінеді: бірінші бөлімі материялық нүкте динамикасы болса, екінші материялық нүктелер жүйесінің динамикасы. 11.2. Масса, материалдық нүкте, күш ұғымдарының негізгі түсініктемесі Материялық нүкте деп қозғалыстың берілген жағдайларында өлшемдерін ескермеуге болатын денені айтамыз. Мұндай дененің кеңістіктегі орны массасы дененің массасына тең массамен жабдықталған геометриялық нүкте орнымен анықталады. Сонымен динамикада, материалдық нүкте күштің әсерінен қозғалысқа ұшырауы қарастырылады. Жүйе динамикасында күштерді топқа бөлу ерекшеліктері қарастырылады. Материялық нүкте динамикасында ішкі күштер деген ұғым жоқ. Ол жерде белгілі немесе белгісіз сыртқы күштердің әсерлері зерттелінеді. Ал жүйе динамикасында олардан басқа тағы да статика бөліміндегідей реакция күштері және ішкі күштер қарастырылады. 11.3. Галилей-Ньютонның механика заңдары. Екпіндік есептеу жүйесі Динамика негізіне, аксиомалар ретінде қабылданатын, бірнеше қағидалар жатады. Бұл қағидалар табиғаттағы құбылыстарға жасал-ған көптеген жылғы бақылаулар мен тәжірибелерді және қоғамдық практика нәтижелерін жалпылап қорытындылаудан алынған. Механика аксиомаларын ең толық және ақырғы түрінде айтып берген И.Ньютон еді. Сондықтан да оларды Ньютон заңдары деп атайды. Ньютоның бірінші заңы (инерция заңы). Егер материялық нүктеге ешбір күш әсер етпесе, онда ол өзінің тыныштық күйін немесе түзу сызықты бірқалыпты қозғалысын сақтайды. Инерция заңында айтылған материялық нүктенің түзу сызықты бірқалыпты қозғалысын инерциялық қозғалыс дейміз. Ньютон заңдары әсіресе инерция заңы орынды болатын координаттар өстерінің жүйелерін инерциялық жүйелер деп атайды. Бұдан былай үнемі инерциялық жүйелер қолданылады. Мұндай жүйелерге қатысты қаралатын денелердің, материялық нүктелердің қозғалыстарын абсолют қозғалыстар деп атайды. Ньютонның екінші заңы (негізгі заң). Материялық нүктеге әсер етуші күш осы нүкте үдеуімен бағытталады және шамасы үдеуге пропорционал болады. . (11.1) Ньютонның үшінші заңы (әсер және қарсы әсер заңы). Материялық екі нүкте бір–біріне оларды қосатын түзу бойымен қарама-қарсы бағытталған, модульдері тең күштерімен әсер етеді. Екі планетаның өзара тартылу күштерін алсақ, олардың да бір біріне тең болып, бір түзудің бойымен қарама-қарсы бағытталатынын көреміз. Мысалға Ай мен Жердің өзара тартылысын алайық (11.1-сурет). Ай А-ны өзіне тартатын жердің күші мен Жер В–ны өзіне тартатын Айдың күші мынадай шартты қанағаттандырады: . Егер бір күшті әсер деп, ал екіншісін қарсы әсер деп атасақ, онда үшінші заңды басқаша былай да айтуға болады. Әрбір әсерге тең және қарама-қарсы бағытталған қарсы әсер болады. Ньютонның төртінші заңы (күш әсерінің тәуелсіздігі туралы заң). Егер материялық нүктеге бір мезгілде бірнеше күш әсер етсе, онда олардың әрқайсысының нүктеге беретін үдеуі сол күш шамасына пропорционал болып, күштердің өзгелеріне және кинематикалық күйіне тәуелсіз болады. Толық үдеу жеке күштер әсерлерінен болатын үдеулердің векторлық қосындысына тең болады. Егер материялық нүктеге бір мезгілде күштері әсер ететін болса, онда бұл күштердің әрқайсысы массасы -ге тең нүктеге өзінің шамасына пропорционал болатын үдеу береді: . Демек, үдеулерінің әрқайсысы тек өзіне сәйкес күші арқы-лы анықталады да, нүктедегі өзге күштерге тәуелсіз болып келеді. Осылайша материялық нүкте бір мезгілде үдеулері әр түрлі қозғалысқа келеді. Кинематикада тағайындалған ереже бойынша бұл қозғалыс үдеулерін өзара геометриялық әдіспен қосуға болады: . Ал мұндағы әрбір үдеудің орнына олардың күш арқылы анықталатын, жоғарыда көрсетілген өрнектерін қойсақ, сонда: . Бір нүктеге түсірілген күштердің теңәсерлі күші болады, ол күштердің геометриялық қосындысына тең: . Демек, нүктенің толық үдеуі: . Осыдан: . (11.2) Сонымен, Ньютонның екінші заңы материялық нүктеге бір мезгілде бірнеше күштер әсер еткенде де орынды болады. Ондағы күшін енді материялық нүктедегі барлық күштердің тең әсерлі күші деп түсіну керек. 11.4. Материалық нүкте динамикасы Әрбір денені материялық нүктелердің жиынтығы деп қарауға болады. Ендеше динамиканы материялық нүкте динамикасынан бастаған жөн. Динамиканың бұл бөлімінде бір ғана материялық нүкте қозғалысының заңдылығы анықталады. Материялық нүкте қозғалысы үшін анықталған заңдылықтарды бірнеше материялық нүктелер жағдайына жалпылай отырып материялық нүктелер жүйесінің заңдылығын аламыз. Осының нәтижесінде қатты дене қозғалысы толық сипаттайтын заңдылықтарды да табуға болады 11.5. Динамика есептері Нүкте динамикасында негізгі екі есеп бар. Оның біріншісінде материялық нүкте қозғалысының заңы және оның массасы m беріледі. Осы заңдылықта болатын қозғалысты тудыратын күшті табу керек болады. Екінші мәселеде берілген күш бойынша массасы m-ге тең нүкте қозғалысының заңын анықтау керек. 11.6. Материялық нүкте қозғалысының декарт координатындағы және табиғи осьтер бойынша дифференциалдық теңдеулері Радиус векторы -ге тең материялық нүктеге әсер етуші күш болсын. Нүкте қозғалысына негізгі заңды қолдансақ алатынымыз: , (11.3) мұндағы, m нүкте массасы, -оның үдеуі. (11.3.)–теңдеуі нүкте динамикасының негізгі теңдеуі деп аталады. Бұл–векторлық теңдеу. Оны әр түрлі координаттар өстеріне проекциялап жазуға болады. Мысалы, оны қозғалмайды деп алынған (3.2-сурет) декарттық координаттар жүйесіндегі өстерге проекциялайық: , немесе: , (11.4) мұндағы, , , -нүкте үдеуінің осы координаттық өстердегі проекциялары, Fx. Fy. Fz нүктеге әсер етуші күштің осы өстердегі проекциялары. (11.4) - теңдеулер материялық нүкте қозғалысының декарттық координаттар өстеріне қатысты алынған дифференциалдық теңдеулері деп аталады. Табиғи өстер бойынша дифференциалдық теңдеулері келесі түрде жазылады: (11.5) 11.7. Заттық нүктесінің бірінші динамикалық есебінің шығарылу жолы Нүкте динамикасының бірінші есебін шешу көп қиыншылық тудырмайды. Бірінші есепте нүкте массасы m және оның қозғалысының кинематикалық теңдеулері: . берілген болады. Осы берілгендер арқылы (3.7) теңдеулерінен іздеп отырған күштің проекциялары табылады: . Осы күш проекциялары арқылы күштің өзін анықтап аламыз. Мысал. Салмағы 1.02 кГ жүк жатқан горизонталь платформа 4 м/с2 үдеумен вертикаль төмен қозғалады (3.3-сурет). Олар бірге қозғалғанда жүктің платформаға түсіретін қысым күшін табу керек. Шешуі. Жүкке бір ғана актив күші түсірілген – оның салмағы . Байланыстардан босату аксиомасын пайдаланып, ойша платформаны алып тастаймыз да, оның әсерін вертикаль жоғары бағытталған реакция күшімен ауыстырамыз. x -өсін вертикаль төмен қозғалыс бағытымен бағыттаймыз (11.3-сурет). Жүктің негізгі теңдеуі мына түрде жазылады: ma = P – N, осы теңдеуден: N = P – ma = 1.02 × 9,8 – 1.02 × 4 = 5.92 Н. Яғни, жүктің платформаға түсіретін қысым күші де 5.92 Н-ға тең болады. 11.8. Екінші динамика есебінің шығарылуы Нүкте динамикасының екінші есебін шешу екінші ретті үш дифференциалдық теңдеулер жүйесі (3.7)-ні интегралдауға келтіріледі. Дифференциалдық теңдеулердің мұндай жүйесінің жалпы шешімі әлі табылмаған. Сондықтан біз ол жүйені шешудің жалпы сұлбасын көрсетіп өтейік. Бізге массасы m-ге тең материялық нүктенің берілген күші әсерінен болатын қозғалысының дифференциалдық теңдеулері (3.7) берілсін: (11.6) . Берілген әсерінен болатын нүкте қозғалысын табу (11.6) дифференциалдық теңдеулер жүйесін шешуге келтіріледі. Ол теңдеулерді түрлендіру нәтижесінде мынадай үш теңдеулер алдық дейік: (11.7) 11.9. Қарапайым интегралдау. Онда (11.7)-ды интегралдау арқылы мынадай бірінші интегралдарды алған болар едік: , , (11.8) . (11.8)-дағы -тұрақтылары интегралдаудың кез келген тұрақтылары деп аталады. (11.8) теңдеулерін тағы да бір рет интегралдап шығуымыз керек. Сол мақсатпен оларды қалай да түрлендіре отырып мынадай түрге келтіре алдық дейік: , , (11.9) . Онда бұларды оңай интегралдаған болар едік те, мынадай қатынастар алар едік: , , (11.10) . мұндағы, - интегралдау тұрақтыларының келесі үшеуі. Уақыт, координаттар, кез келген тұрақты шамалар арасындағы тәуелділікті беретін және қозғалыс теңдеулері негізінде орынды болатын, (11.10) түріндегі қатынастарды қозғалыс теңдеулерінің екінші интегралдары деп атайды. (11.10) қатынастарынан -терді табуға болады: , , (11.11) . (11.11) теңдіктері (11.6) қозғалыс теңдеулерінің жалпы шешімі болып табылады. Мұнда нүкте координаттары уақытқа және алты кез келген тұрақты шамаларға тәуелді функциялар ретінде анықталған. 11.10. Интегралдық тұрақты шамалар; бастапқы шартты қолданып, оларды табу Сонымен, жалпы жағдайда нүкте координаттары алты кез келген тұрақты шамаларға тәуелді болып шықты. Басқаша айтқанда, қозғалыс теңдеулерін интегралдау арқылы материялық нүктенің берілген күш әсерінен мүмкін болатын қозға-лыстарының барлығының да заңдарын табуға болады екен. Мысалы, біз материялық нүктені ауасыз ортада бір орыннан әр түрлі бағыттағы жылдамдықпен ұшыруымызға болады. Онда ол нүкте ауырлық күші әсерінен бастапқы жылдамдықтың қалай бағытталуына байланысты түзу сызық бойымен немесе әр түрлі параболалар бойымен қозғалуы мүмкін. Сол себепті күштің өзгеру заңдылығын: , көрсетумен қатар, нүктенің бастапқы орны мен жылдамдығын да нақтылы көрсетіп отыруымыз қажет. Уақыт болғанда, нүктенің бастапқы орнын анықтайтын координаттар мынадай болды дейік: . (11.12) Ал бастапқы жылдамдық проекциялары мынадай болсын: . (11.13) (11.12) және (1.13) қатынастарының жиынын бастапқы шарттар деп атаймыз. Осы бастапқы шарттар арқылы интегралдау тұрақтылары табылады. Ол үшін (11.8) және (11.10) теңдеулердегі айнымалылары орнына олардың (11.12) және (11.13)-теңдеулерде көрсетілген бастапқы мәндерді қоямыз. Сонда: , , , (11.14) , , . (11.14) бойынша анықталатын интегралдау тұрақтыларының мәндерін (11.11) –теңдеуге қойсақ, мынаны аламыз: , , (11.15) . (11.15)-теңдіктер берілген күш әсерінен болатын және бастапқы шарттарға сәйкес орындалатын нүкте қозғалысының заңын анықтайды. Сонымен, нүкте динамикасының екінші есебінің шешілуі осы сұлба бойынша жүргізіледі. 1-мысал. Массасы –ге тең, бойында электрдің е заряды бар материялық нүкте кернеуі болатын біртекті электр өрісінде орналасқан. Мұндағы, А және k берілген тұрақты шамалар. Электр өрісінде материялық нүктеге бағыты кернеуіне қарай бағытталған күш әсер етеді. Нүктенің бастапқы орнын координаттардың бас нүктесі ретінде қабылдап, оның қозғалысын анықтау керек. Салмақ күшінің әсерін ескермей, бастапқы жылдамдығын нөлге тең деп санауға болады (11.4-сурет). Шешуі. Материялық нүктеге әсер етуші бір ғана күш бар, ол . Нүкте қозғалысы – түзу сызықты қозғалыс. Бойымен нүкте қозғалатын түзуді өсі ретінде қабылдаймыз. Нүкте қозғалысын сипаттайтын дифференциалдық теңдеу біреу ғана: Осы дифференциалдық теңдеудің айнымалы шамаларын ажыратып жазамыз: Теңдеу бір рет интегралданғаннан кейін мына түрге келеді: ді табу үшін бастапқы мәндер шамаларын жоғарыдағы өрнегіне апарып қоямыз. Сонда: Алдыңғы теңдікке мәнін қойып оны қайта жазуға болады: Соңғы теңдеуден: , мұндағы, тұрақты -нің нөлге тең екендігін, болғанда болатын бастапқы шарттан анықтаймыз. Сонымен, М нүктенің қозғалыс заңы мына өрнекпен беріледі: . 2-мысал. Массасы тең М нүкте үйкеліссіз көлбеу жазықтық пен кедергілі ортада қозғалсын. Орта кедергісі жылдамдықтың бірінші дәрежесіне пропорционал болсын мұндағы k=2 тұрақты шама, α=300 (11.5-сурет). Нүктенің қозғалыс заңын анықтау керек. Шешуі. өсін келбеу жазықтық бойымен бағыттайық. Нүктенің қозғалыс теңдеуі: ( ) ( ) теңдеуіндегі және айнымалыларды ажыратып жазамыз: (б) (б)-теңдеуді бір рет интегралдап мынадай теңдеу аламыз: (в) болғанда, (г) Бұл бастапқы мәндерді (в) теңдеуіне қойсақ: Олай болса (в) теңдеуі мына түрде қайта жазылады: Осыдан: (ж) (ж) теңдеуді тағы бір рет интегралдап мынаны аламыз: (з) (г)-дегі бастапқы шарттарды пайдалана отырып (з) теңдеуінен Сә тұрақтысын табамыз: Осыны ескеріп (з) теңдеуін қайта жазамыз: (и) Мәндерін орнына қойсақ: аламыз. № 12 ДӘРІС. МАТЕРИЯЛЫҚ НҮКТЕНІҢ ТЕРБЕЛІСІ. 12.1. Заттық нүктенің түзу сызықты еркін тербелісі. Айталық, массасы m- ге тең болған М материялық нүктеге барлық уақытта оны теп-теңдік қалпына қарай бағыттаған күш әсер етсін және осы нүкте түзу сызықты қозғалыста болсын (15.1-сурет). 15.1 сурет Материялық нүкте координатасының функциясы ретінде алынған айнымалы және тепе-теңдік қалпына қарай бағытталған күш қайтарушы күш деп аталады. Қайтарушы күш нүктенің тұрған орнына байланысты болады, яғни: Ғ= - сх. (15.1) Мұндағы с - материялық нүктені ұзындық бірлігіне өткізу үшін қажет болатын күш, ол серпімділік коэффиценті делінеді, оның өлшем бірлігі Н/м, х- нүктенің абциссасы. Бастапқы уақытта М нүктесінің абциссасы х0 жылдамдығы V0 болсын. М нүктенің қозғалыс диффренциалдық теңдеуін құрамыз: m = - cx (15.2) Бұл өрнекке к2 = (15.3) белгілеуін енгізсек, онда (15.2) өрнегі төмендегідей жазылады: + к2х=0 (15.4) (15.4)- тің жалпы шешімі төмендегідей болады: (15.5) (15.5)-тегі С1 және С2 тұрақты шамалар бастапқы шарттардан пайдаланылып анықталады, яғни (15.6) Сонымен, М нүкте қозғалысы (15.7) теңдеуімен анықталады. Материялық нүктенің тербелмелі қозғалысын жалпы түрде зерттеу қолайлы болуы үшін С1, С2орнына а және тұрақтыларды төмендегідей таңдаймыз: (15.8) (15.8)-ді (15.5)-ке қойып, М нүктенің қозғалысын анықтайтын теңдеуді төмендегі түрге келтіреміз: (15.9) (15.8)-дегі өрнектерді квадратқа шығарып қоссақ, соңынан (15.8)-дің екіншісін біріншісіне мүшелеп бөлсек және (15.6) ны есепке алсақ, онда (15.10) келіп шығады. (15.9)-дан көретініміз, материялық нүктенің қайтарушы күш әсеріндегі қозғалысы периодтық сипатқа ие болатын еркін тербелмелі қозғалыстан тұрады екен. Олай болса (15.4) өрнегі нүктенің еркін тербелмелі қозғалысының дифферренциалдық теңдеуін береді, яғни (15.9) теңдеуі материялық нүктенің еркін тербелмелі қозғалыс заңын өрнектейді. (15.9) теңдеудегі а - нүктенің тепе-теңдік қалпыынан ең үлкен ауытқуы-тербеліс амплитудасы,кt+ - тербеліс фазасы, - бастапқы фаза, к - тербелістің бұрыштық (дөңгелектік) жиілігі делінеді. 15.2 сурет Еркін тербелмелі қозғалыс графигі 15.2 суретте көрсетілген. период аралығында тербеліс фазасының 2 -ге өзгеруін есепке алатын болсақ, (2.9)-дан төмендегі теңдеуді жазуға болады: k(t+ )+ =kt+( +2 ). Бұдан еркін тербелмелі қозғалыстың периодын анықтайтын = (15.11) формуланы шығарып аламыз. Тербеліс периодының кері мәніне тербеліс жиілігі делінеді, оны мен белгілесек, анықтамаға сәйкес: . (15.10),(15.11) дан көретініміз, тербеліс амплитудасы және бастапқы фаза қозғалыстың бастапқы шарттарына байланысты, тербеліс периоды, сондай-ақ тербеліс жиілігі нүктенің бастапқы орнына байланысты емес екен.Тербеліс периоды тербелмелі қозғалыстағы нүктенің өзгермейтін сипаттамасы. Тербеліс периодын табу үшін тербелмелі қозғалыстың дифференциалдық теңдеуін (15.4) түрінде құру және к - ны табу жеткілікті. 12.2. Кедергі жылдамдыққа үлесті (пропорционал) болғандағы кедергісіз ортада нүктенің еріксіз тербелісі. Резонанс жағдайы. Материялық нүкте қайтарушы күш және де уақыттың үздіксіз функциясы ретінде алынған айнымалы және мәжбүрлеуші (ұйытқытушы-оятушы) күш деп аталатын күш әсерінде түзу сызықты қозғалыста 15.6-сурет болсын (15.6-сурет). Оятушы үш гармоникалық заң бойынша өзгерсін,яғни: (15.34) (15.34)-де Q оятушы күштің ең үлкен мәні, р-дөңгелектік жиілігі, , pt+ - фазасы, -бастапқы фазасы.Ал, оятушы күш периоды ға тең. Бастапқы уақытта М нүкте М0 де болып,оның координатасы х0, жылдамдығы V0 болсын. Материялық нүктенің қозғалыс дифференциалдық теңдеуін құрамыз: (15.35) (15.35)-ті төмендегі түрде жазамыз: белгілеулер енгізсек, (15.36) келіп шығады. Дифференциалдық теңдеулер теориясынан, (15.36) теңдеудің шешімі төмендегідей жазылады: х=x1+x2 (15.37) (15.37)-де х1-мен (15.38) бір текті дифференциалдық теңдеудің жалпы шешімі, ал х2 арқылы (15.36)-ның дербес шешімі белгіленген. (15.38) дифференциалдық теңдеулердің жалпы шешімі (15.39) түрінде өрнектелуі белгілі. (15.36) тұрақты коэффициентті сызықты біртекті дифференциалдық теңдеудің дербес шешімін төмендегі түрде аламыз: (15.40) (15.40)- тағы В коэффициентті анықтау үшін (15.40)-тан уақыт бойынша екінші ретті туынды аламыз: (15.41) (15.40) және (15.41)-ді (15.36)-ға қоямыз: Бұл теңбе-теңдіктен: Нәтижеде (15.40) теңдеуі төмендегідей жазылады: (15.42) (15.42) теңдеуімен анықталатын қозғалыс материялық нүктенің мәжбүр болған (еріксіз) тербелмелі қозғалысы делінеді. Демек, (15.36) ның жалпы шешімі төмендегідей жазылады: (15.43) (15.43) тағы а және қозғалыстың бастапқы шарттарынан анықталады. (15.42) ден көретініміз, мәжбүр болған тербелмелі қозғалыстың амплитудасы немесе нүктенің ең үлкен динамикалық жылжыуы: (15.44) болады. (15.44) тен пайдаланып, (15.42) ні төмендегі түрде жазуымыз мүмкін: егер к>p болса; егер к<p болса Бұл қатнастарға сәйкес к>p болғанда мәжбүрлі тербеліс фазасы оятушы күш фазасымен бірдей болады. Ал к<p жағдайында мәжбүрлі тербеліс фазасы оятушы күш фазасынан - ге артта қалады. Мәжбүрлі тербеліс амплитудасы мен p/k арасындағы байланысты, қарастырайық. Бұл үшін (15.44)-ті төмендегідей түрге келтіреміз: (15.45) Мұндағы lст =P0/k2 материялық нүктенің оятушы күштің максимал мәні Q0 әсерінде алған статикалық жылжыуы белгіленген. (15.44)-тен көретініміз, мәжбүрлі тербеліс амплитудасы оятушы күшке және еркін тербелістің дөңгелектік жиілігіне байланысты екендігі. Материялық нүктенің динамикалық жылжуының статикалық жылжуына қатынасы динамикалық коэффицент делінеді. Оны мен белгілейміз. (15.46) Динамикалық коэффициент мен арасындағы (15.46) байланыс 15.7-сурет графигі 15.7 суретте бейнеленген. Бастапқы шарттар , болатын жағдайдағы қозғалысты зерттеу үшін (15.36) дифференциалдық теңдеудің жалпы шешімін төмендегі түрде жазамыз; (15.47) (15.47)-ден уакыт бойынша туынды аламыз; (15.48) Материялык нукте қозғалысының бастапқы шарттарын (15.47) және (15.48)-ге қойсақ; (15.49) келіп шығады. (15.49)-дан табылады. Демек (15.47) төмендегідей түрде жазылады; (15.50) (15.49) дан көретініміз, және де р к болғанда тербеліс өзіне тән түрге не болады. Бұл жағдай "Резонанс" жағдайы деп аталады. "Резонанс" жагдайының теңдеуі; , немесе (15.51) (15.51) теңдеуімен өрнектелетін қозғалыстың дөңгелектік жиілігі , период амплитудасы периодтық функция ретінде айнымалы тербелмелі козғалыстан тұрады деу мумкін. Бұл тербелістің амплитудасы: Бұл амплитуданың периоды Және ол T- ға қарағанда едауір үлкен болады. (15.51) графигі 15.8 суретте көрсетілген. Еріксіз және еркін тербелістердің дөңгелектік жиіліктері бірдей болған ( ) жағдай резонанс жағдайы деп аталады. 15.8 сурет болғанда (15.36) дифференциалдық теңдеу төмендегідей жазылады; (15.52) Резонанс жагдайында (15.52) теңдеудің дербес шешімін төмендегі түрде анықтаймыз: (15.53) (15.53)-тен уақыт бойынша туынды аламыз: (15.54) (15.53) және (15.54)-ті (15.52)-ге қойсақ; ) (15.55) болады. (15.55)-тен келіп шығады. Демек, (15.52) дифференциалдық теңдеудің жалпы шешімі төмендегідей болады; . (15.56) (15.56)-дан көретініміз, нуқтенің қозғалысы еркін және мәжбүрлі тербелістердің қосындысынан тұрады екен. Резонанс жагдайындағы мәжбүрлі тербелмелі қозғалыс теңдеуі (15.57) болады. (15.57)-де мәжбүрлі тербелістің амплитудасы, фазасы, ал деңгелектік жиілігі. (15.57)-ге сәйкес, резонанс жатдайындағы мәжбүрлі тербелістің фазасы оятушы күш фазасынан -ге артта қалады, ал амплитуда уақытқа пропорционал өзгереді. 15.9 сурет 15.10 сурет (15.57) теңдеуімен анықталатын козғалыс графигі 15.9-суретте бейнеленген. №13 ДӘРІС. МАТЕРИЯЛЫҚ НҮКТЕНІҢ САЛЫСТЫРМАЛЫ ҚОЗҒАЛЫСЫ. Заттық нүктенің салыстырмалы қозғалыстағы дифференциалдық теңдеулері. Көшірмелі және Кориолис екпіндік күштері. .Классикалық механикада салыстырмалық қағидасы (принципі). Салмақсыздық құбылыс. Кинематикадан бізге белгілісі, қатты дененің жазық-паралелль қозғалысы осы денеде полюc деп алынған нүктенің кез-келген уақыттағы алатын орны және дененің осы нүктеден өтетін өсь төңірегінде айналған кездегі бұрылу бұрышы арқылы анықталады. Дененің инерция центрін полюc деп қабылдасақ, жазық-паралелль қозғалатын дененің кез-келген уақытта алатын орны инерция центрінің координаттары және бұрылу бұрышы арқылы анықталады. Дене , , , ..., күштер әсерінде қозғалатын болсын (17.1-сурет). Бұл жағдайда нүктенің қозғалысын дене инерция центрінің 17.1-сурет қозғалысы туралы теоремадан пайдаланып анықтау мүмкін: (17.1) Ал, дененің полюcке қатысты қозғалысы қозғалыс жазықтығына перпендикуляр болатын және нүктеден өтетін Sz өсі төңірегіндегі айналмалы қозғалысының дифференциалдық теңдеуімен өрнектеледі: (17.2) белгілеулер енгізсек, қатты дененің жазық- паралелль қозғалысының дифференциалдық теңдеулерін төмендегідей өрнектеу мүмкін: (17.3) (17.3) көрінісіндегі дифференциалдық теңдеулер Декарттық координаттар жүйесінде төмендегідей жазылады: (17.4) Дене масса центрінің траекториясы анық болса, нүкте қозғалысын табиғи координаттар жүйесінде де анықтау мүмкін. Бұл жағдайда (17.4) дифференциал теңдеулер жүйесі (17.5) түрінде болады. Мұндағы инерция центрі траекториясының қисықтық радиусы. № 14 ДӘРІС. ЖҮЙЕ ДИНАМИКАСЫНА КІРІСПЕ.
|
|
|
|
|
|
|
|
|
|
|
|
ЕКПІНДІК МОМЕНТТЕР.
14.1. Механикалық жүйе Материялық нүктелердің механикалық жүйесі деп қозғалыс-тары өзара тәуелді болып келетін материялық нүктелер жиынтығын айтады. Мұндай жиынтықтағы әрбір жеке нүкте қозғалысы ондағы барлық басқа нүктелердің қозғалыстары мен олардың орындарына тәуелді анықталады. Материялық нүктелердің механикалық жүйесіне мысал ретінде күн жүйесін алуға болады. Күн жүйесіндегі әрбір жеке планета қозғалысы Күннің және бұл жүйе құрамына енетін барлық қалған планеталардың қозғалыстарына және орындарына байланысты анықталады.
Егер қозғалыс кезінде жүйедегі нүктелердің бір-бірінен ара қашықтықтары өзгермей сақталатын болса, онда бұл жүйені өзгермейтін механикалық жүйе дейміз. Абсолют қатты дене өзгермейтін механикалық жүйе ретінде қарастырылады. Демек, механикалық жүйенің айрықша белгісі - оның нүктелерінің арасында өзара әсерлесу күшінің бар екендігі. Осыған қарағанда материялық нүктелердің кез келген жиынтығы механикалық жүйе құра алмайтындығы белгілі. Механикалық жүйедегі әрбір нүктенің қозғалысы біріне – бірі тәуелді. Бұдан былай материялық нүктелердің механикалық жүйесі деп толық айтып жатпай, оны қысқаша нүктелер жүйесі немесе механикалық жүйе деп атайтын боламыз.
Нүктелердің кеңістікте орын ауыстыру еркіндіктері шектелмеген материялық нүктелердің механикалық жүйесін еркін жүйе дейміз. Еркін механикалық жүйе нүктелері кеңістіктің кез келген жерінде бола алады және кез келген жылдамдықты қабылдай алады. Еркін механикалық жүйенің мысалы ретінде Күн жүйесін алуға болады.
Егер нүктелердің еркін қозғалуын тежеп отыратындай алдын ала жүйеге қосымша шарттар қойылған болса, онда оны еркін емес механикалық жүйе деп атаймыз.
14.2. Жүйе массасы; масса ортасы (центрі) Механикалық жүйе динамикасында жиі қолданылатын негізгі ұғымдардың бірі массалар центрі туралы ұғым. Енді осы ұғымға тоқталып өтейік. Ол үшін материялық нүктелерден тұратын механикалық жүйе алайық. Оның қозғалысы OXYZ инерциялық өстер жүйесіне қатысты қарастырылатын болсын. Массасы  , ал радиус-векторы
, ал радиус-векторы  -ға тең,
-ға тең, 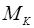 нүктесін алайық.
нүктесін алайық.
 Механикалық жүйе массасы деп ондағы нүктелер массаларының қосындысына тең болатын шаманы айтамыз:
Механикалық жүйе массасы деп ондағы нүктелер массаларының қосындысына тең болатын шаманы айтамыз: 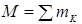 . (14.1)
. (14.1)
Механикалық жүйе массаларының центрі деп радиус векторы:  . (14.2)
. (14.2)
формуласымен анықталатын геомет-риялық нүктені (С-ны) айтамыз (14.1-сурет). Егер жүйе нүктелерінің коор-динаттарын  деп алсақ, онда оның массалары центрі С-ның коорди-наттары мынадай формулаларымен анықталады:
деп алсақ, онда оның массалары центрі С-ның коорди-наттары мынадай формулаларымен анықталады:


 . (14.3)
. (14.3)
Кейде бұл нүктені механикалық жүйенің инерциялар центрі деп атайды. Сонымен, жүйе динамикасында, статикада анықталған ауырлық центрі деген ұғымнан басқа, массалар (инерциялар) центрі-ауырлық центріне қарағанда кең мағыналы ұғым. Жоғарыдағы анықтамасына қарағанда механикалық жүйенің массалары центрінің әрбір уақыт кезеңінде кеңістіктегі орны тек жүйедегі нүктелер массалары мен ол нүктелердің кеңістіктегі орналасуларына ғана тәуелді. Егер жүйе нүктелері үшін еркін түсу үдеуі g тұрақты шама болса, онда нүктелердің массаларын олардың салмақтары арқылы анықтаймыз: 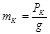
 . Жүйе массасы М және оның салмағы
. Жүйе массасы М және оның салмағы  мынадай қатынаста болатындығын, яғни
мынадай қатынаста болатындығын, яғни  формуласын ескере отырып, (14.2) формуласын мына түрге келтіре аламыз:
формуласын ескере отырып, (14.2) формуласын мына түрге келтіре аламыз:
 . (14.4)
. (14.4)
Сөйтіп, бұл дербес жағдайда (g = const) (14.2) формуласы статикада ауырлық центрін анықтайтын (14.4) формуласына айналады.
14.3. Күштерді топқа бөлу; ішікі күштер ерекшелігі Динамиканың барлық заңдары еркін материялық нүкте үшін орынды болғандықтан, олар тек еркін механикалық жүйеге ғана арнайы қолданылады. Ал оларды еркін емес механикалық жүйе динамикасының мәселелерінде де қолдану мүмкіндігін туғызу үшін жүйені байланыстардан ажырату (бастау) аксиомасын пайдалануымыз керек. Жүйені байланыстардан ажырату аксиомасын (принципін) былай айтамыз: қандай да бір қозғалыстағы еркін емес материялық нүктелердің механикалық жүйесінің әрбір нүктесінде берілген (актив) күштермен қатар байланыстар реакцияларын да түсіруіміз керек. Сонда бұл жүйені актив күштер мен байланыстар реакциялары әсер ететін еркін механикалық жүйе деп қарауға болады. Қатты денеге әсер етуші күштерді актив (берілген) және пассив (байланыстар реакциялары) күштер деп аталатын екі топқа бөліп келдік. Жүйе динамикасында күштерді топтарға бөлудің тағы бір тәсілі қолданылады. Ол – механикалық жүйе нүктелеріне әсер ететін барлық күштерді сыртқы және ішкі күштерге бөлу жөніндегі тәсіл.
Берілген механикалық жүйенің сыртқы күштері деп осы жүйе құрамына енбейтін сыртқы жүйе нүктелеріне жасайтын әсерлерінен туатын күштерді айтамыз және  деп белгілейміз.
деп белгілейміз.
Берілген механикалық жүйе нүктелерінің арасында болатын өзара әсерлесу күштерін ішкі күштер дейміз және  деп белгілейміз.
деп белгілейміз.
Ішкі күштер берілген жүйе нүктелерінің арасындағы өзара әсер етуші күштер болғандықтан оларға Ньютонның 3-ші заңын қолдана аламыз. Осыдан жүйенің қос – қостан алынған ішкі күштері шама жағынан тең, бір түзу бойымен бір-біріне қарама-қарсы бағытталған күштер жүйесінің бас векторы және кез келген центрге қатысты алынған, олардың бас моменті үнемі нөлге тең болады:
 ,
, 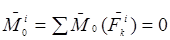 . (14.5)
. (14.5)
Бұл ішкі күштердің маңызды қасиеті, яғни ішікі күштердің ерекшелігі болып табылады.
ЕКПІНДІК МОМЕНТТЕР.
Осьтік екпіндік моменті. Екпіндік радиусы.
 Масса центрінің орны жүйеде масса үлестірімін толық сипаттамайды. Мысалы: Oz өстен h қашықтықта тұратын екі бірдей А және В шарлардың орнын бірдей қашықтыққа өзгертсек (14.2-сурет), жүйе масса центрінің орны өзгермейді. Бірақ жүйеде масса үлестірімі өзгереді, яғни А және В шарлардың Oz өсь төңірегінде айналуы жылдамдайды не баяулайды.
Масса центрінің орны жүйеде масса үлестірімін толық сипаттамайды. Мысалы: Oz өстен h қашықтықта тұратын екі бірдей А және В шарлардың орнын бірдей қашықтыққа өзгертсек (14.2-сурет), жүйе масса центрінің орны өзгермейді. Бірақ жүйеде масса үлестірімі өзгереді, яғни А және В шарлардың Oz өсь төңірегінде айналуы жылдамдайды не баяулайды.
Механикалық жүйенің (жүйеның) айланған кездегі оның массасының үлестірілуін анықтайтын шама инерция моменті деп аталады. Жүйеның
 өске, нүктеге және жазықтыққа қатысты инерция моменттері ұғымдарымен танысып шығайық. Бұл үшін кез келген О нүктеден өтетін бір-біріне перпендикуляр үш өсті және үш жазықтықты алайық (14.3-сурет). Жүйеның өске қатысты инерция моменті деп сол жүйенің әрбір бөлшегінің массасын осы бөлшектен өске дейінгі болған жақын арақашықтықтың квадратына көбейткендегі пайда болған шаманы бүтін жүйе бөлшектері бойынша алып қосқанға айтады.
өске, нүктеге және жазықтыққа қатысты инерция моменттері ұғымдарымен танысып шығайық. Бұл үшін кез келген О нүктеден өтетін бір-біріне перпендикуляр үш өсті және үш жазықтықты алайық (14.3-сурет). Жүйеның өске қатысты инерция моменті деп сол жүйенің әрбір бөлшегінің массасын осы бөлшектен өске дейінгі болған жақын арақашықтықтың квадратына көбейткендегі пайда болған шаманы бүтін жүйе бөлшектері бойынша алып қосқанға айтады.
Механикалық жүйенің Oz өсіне қатысты инерция моментін 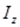 деп белгілесек, онда берген анықтамаға сәйкес
деп белгілесек, онда берген анықтамаға сәйкес
 . (14.6)
. (14.6)
Бұл жердегі  нүктеден өске дейінгі болған арақашықтық.
нүктеден өске дейінгі болған арақашықтық.
Инерция моментінің СИ жүйедағы өлшем бірлігі кгм2,техникалық жүйеде кгмс2 болады. Өске қатысты инерция моментін есептегенде жүйе бөлшектерінен өске дейінгі болған арақашықтықты осы бөлшектердің координаталары арқылы өрнектеуге болады. Егер  нүктенің координаталарын
нүктенің координаталарын  деп белгілесек, онда жүйеның Ox, Oy, Oz өстерге қатысты инерция моменттері төмендегідей жазылады:
деп белгілесек, онда жүйеның Ox, Oy, Oz өстерге қатысты инерция моменттері төмендегідей жазылады:
 (14.7)
(14.7)
Жүйеның координаталар басына қатысты инерция моменті
 (14.8)
(14.8)
болады.
Егер (14.7) өрнектерді бір-бірімен өзара қосып, табылғанды (16.11) мен салыстырсақ төмендегідей байланыс шығады:
 (14.9)
(14.9)
Жүйеның yOz, xOz және xOy жазықтықтарға қатысты инерция моменттері
 (14.10)
(14.10)
формулалардан табылады.
Бір текті дененің кез келген өске қатысты инерция моментін оның осы өске қатысты инерция радиусы деп аталатын сызықтық шама  ны пайдаланып та анықтауға болады, яғни
ны пайдаланып та анықтауға болады, яғни 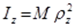 (14.11)
(14.11)
 Бір текті дененің өске қатысты иенрция радиусы тәжірибелер көмегінде анықталып, кестелерде берілген болады.
Бір текті дененің өске қатысты иенрция радиусы тәжірибелер көмегінде анықталып, кестелерде берілген болады.
Егер дененің кезкелген өске қатысты инерция моменті анық болса , оның осы өске қатысты инерция радиусын (14.11)-ке сәйкес
 (14.12)
(14.12)
формуладан анықтау мүмкін.
Қатты дененнің центрден тепкіш инерция моменттері төмендегідей табылады:
 (14.12)
(14.12)
14.5. Параллель оське қарасты екпіндік момент.
Гьюгенс-Штейнер теоремасы. Дененің берілген өске қатысты моменті массалар центрі арқылы өтетін параллель өске қатысты екпіндік моментіне дене массасын бұл екі өстің ара қашықтығының квадратына көбейтіп қосқанға тең болады (14.4-сурет).

14.6. Қарапайым денелердің екпіндік моменті.
| Дене түрі | Дене формасы | Инерция моменті | Дене түрі | Дене формасы | Инерция моменті |
| 1 | 2 | 3 | 1 | 2 | 3 |
| Жіңішке стержень | 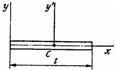
| 
| Тік бұрышты пирамида | 
| 
|
| Тік төртбұрыш | 
| 
| Дөнгелек цилиндр | 
| 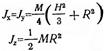
|
| Эллипс | 
| 
| Дөңгелек конус | 
| 
|
| Тік бұрышты паралле-лепипед | 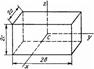
| 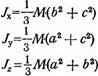
| Эллипсоид | 
| 
|
№15 ДӘРІС. МАТЕРИЯЛЫҚ НҮКТЕ ЖӘНЕ МАТЕРИЯЛЫҚ ЖҮЙЕ ДИНАМИКАСЫНЫҢ ЖАЛПЫ ТЕОРЕМАЛАРЫ.
15.1. Механикалық жүйе қозғалысының дифференциалдық теңдеулері
1. Еркін механикалық жүйе. Қандайда инерциялық координаттар жүйесіне қатысты алынған n материялық нүктелерден тұратын механикалық жүйе қозғалысын қарастырайық. Осындағы массасы  -ға тең нүкте
-ға тең нүкте  -ны жекелеп алайық та, оған әсер ететін сыртқы күштер мен ішкі күштердің тең әсерлі күштерін
-ны жекелеп алайық та, оған әсер ететін сыртқы күштер мен ішкі күштердің тең әсерлі күштерін 
 және бұл нүктенің радиус-векторы
және бұл нүктенің радиус-векторы  болсын.
болсын.  – нүктесінің қозғалыс теңдеуін вектор түрінде жаза аламыз:
– нүктесінің қозғалыс теңдеуін вектор түрінде жаза аламыз:
 . (15.1)
. (15.1)
Мұндай теңдеу жүйедегі әрбір нүкте үшін де жазылады. Сонда (3.59) – теңдеулер жүйесі еркін механикалық жүйе қозғалысының векторлық түрдегі дифференциалдық теңдеулері. Егер осы векторлық теңдеулердің әрқайсысын OX, OY, OZ қозғалмайтын координаттық өстерге проекциялайтын болсақ, онда еркін механикалық жүйе қозғалысының координаттық түрдегі дифференциалдық теңдеулерін аламыз:
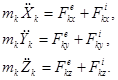
 (15.2)
(15.2)
2. Еркін емес механикалық жүйе. Бізге n материялық нүктелердің еркін емес механикалық жүйесі берілген болсын. Оның қандайда бір  нүктесіне әсер ететін сыртқы және ішкі актив күштердің тең әсерлі күшін
нүктесіне әсер ететін сыртқы және ішкі актив күштердің тең әсерлі күшін  -деп алайық. Байланыстардан ажырату туралы аксиомаға сүйене отырып берілген еркін емес механикалық жүйенің әрбір нүктесіне байланыстар реакцияларын түсіреміз.
-деп алайық. Байланыстардан ажырату туралы аксиомаға сүйене отырып берілген еркін емес механикалық жүйенің әрбір нүктесіне байланыстар реакцияларын түсіреміз.  нүктесіне түсетін байланыстар реакцияларының барлығына тең әсерлі күш
нүктесіне түсетін байланыстар реакцияларының барлығына тең әсерлі күш  болсын. Жүйе нүктелерінің әрқайсысына актив күштерге қоса осылайша байланыстар реакцияларын түсіргеннен соң оны еркін механикалық жүйе деп алуға болады. Сол себепті бұл механикалық жүйенің әрбір нүктесіне Нъютонның II және III заңдарын қолдана аламыз. Сонда еркін емес механикалық жүйе қозғалысының векторлық теңдеулері мына түрде жазылады:
болсын. Жүйе нүктелерінің әрқайсысына актив күштерге қоса осылайша байланыстар реакцияларын түсіргеннен соң оны еркін механикалық жүйе деп алуға болады. Сол себепті бұл механикалық жүйенің әрбір нүктесіне Нъютонның II және III заңдарын қолдана аламыз. Сонда еркін емес механикалық жүйе қозғалысының векторлық теңдеулері мына түрде жазылады:  ,
,  (15.3)
(15.3)
Бұл векторлық теңдеулердің әрбіреуінің екі жағын да қозғалмайтын O X , O Y , O Z координаттар өстеріне проекциялау арқылы еркін емес механикалық жүйе қозғалысының дифференциалдық теңдеулерін координаттық түрде аламыз:
 ,
,
 ,
,  (15.4)
(15.4)

15.2. Жүйенің массалар ортасы қозғалысы туралы теорема. Бұл теореманы дәлелдеу үшін механикалық жүйе қозғалысының дифференциалдық теңдеулерін еске түсірейік:

 .
.
Осы теңдеулердің барлығын бір-біріне қосайық, сонда алатынымыз:
 . (15.5)
. (15.5)
Бұл теңдіктің оң жағындағы қосындылардың екіншісі, ішкі күштер қосындысы, нөлге тең. Ал оның сол жағындағы қосындыны (14.2) формуласын ескере отырып, мына түрге келтіре аламыз:
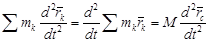 . (15.6)
. (15.6)
Сондықтан (15.5) – теңдеуден іздеп отырған теореманың өрнегі мына түрге келеді:
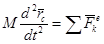 немесе
немесе 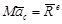 . (15.7)
. (15.7)
(15.7) теңдігі жүйенің массалар центрінің қозғалысы туралы теореманы өрнектейді. Ол теорема былай айтылады: механикалық жүйенің массалары центрі материялық нүкте сияқты қозғалады. Бұл нүктенің массасы тұтас жүйенің массасына тең, ал оған әсер етуші күш механикалық жүйенің сыртқы күштерінің бас векторына тең болады. (15.7) векторлық теңдеуді координаттық өстерге проекцияласақ, мынадай үш скаляр теңдеу аламыз:
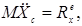

 , (15.8)
, (15.8)
мұндағы, Xc, Yc, Zc – массалар центрінің үдеуінің координаттар өстеріндегі проекциялары. (15.8) үш скаляр теңдеу -массасы М-ге тең және 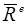 күші әсер ететін массалар центрі С нүктесі қозғалысының дифференциалдық теңдеулері. Өзінің құрамы жағынан бұл теңдеулер нүкте динамикасының осыған сәйкес теңдеулерінен ешқандай айырмашылығы жоқ. Сондықтан да жүйе массалары центрінің қозғалысын зерттеу мәселесі нүкте динамикасының мәселесіне жатады.
күші әсер ететін массалар центрі С нүктесі қозғалысының дифференциалдық теңдеулері. Өзінің құрамы жағынан бұл теңдеулер нүкте динамикасының осыған сәйкес теңдеулерінен ешқандай айырмашылығы жоқ. Сондықтан да жүйе массалары центрінің қозғалысын зерттеу мәселесі нүкте динамикасының мәселесіне жатады.
Массалар ортасы қозғалысының сақталу заңы. Егер жүйенің сыртқы күштерінің бас векторы нөлге тең болса, онда массалар центрі тұрақты жылдамдықпен қозғалады. Шынында  болса, (15.8) - теңдіктен:
болса, (15.8) - теңдіктен:
 . (15.9)
. (15.9)
Осыдан:  . (15.10)
. (15.10)
(15.10) – векторлық теңдікті жүйенің массалары центрі С-ның жылдамдығының сақталу заңы деп атайды.
1-мысал. Біртекті конус горизонталь жазықтықтың бетінде дөңгелеп қозғалады (15.1-сурет). Конустың 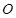 төбесі қозғалмайды, ал оның биіктігі
төбесі қозғалмайды, ал оның биіктігі  вертикаль
вертикаль  өсін бірқалыпты
өсін бірқалыпты  жиілікпен айнала қозғалады. Конустың салмағы
жиілікпен айнала қозғалады. Конустың салмағы  , ал биіктігі
, ал биіктігі 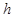 . Конустың биіктігі мен жасаушысының арасындағы бұрыш
. Конустың биіктігі мен жасаушысының арасындағы бұрыш  .
.
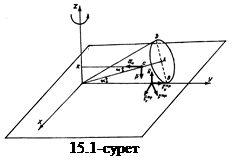 Жазықтық пен конустың арасындағы үйкеліс күшін анықтау керек.
Жазықтық пен конустың арасындағы үйкеліс күшін анықтау керек.
Шешуі. Конустың массалар центрінің қозғалысын қарастырамыз. Конус біртекті болғандықтан, оның ауырлық центрі  биіктігі
биіктігі  -ның бойында орналасқан және
-ның бойында орналасқан және  . Есептің берілгені бойынша ауырлық центрінің
. Есептің берілгені бойынша ауырлық центрінің  үдеуі
үдеуі  өсіне қарай, осы өске перпендикуляр
өсіне қарай, осы өске перпендикуляр  бойымен бағытталады.
бойымен бағытталады.  үдеудің шамасы:
үдеудің шамасы:  , мұндағы
, мұндағы 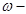 конус биіктігі
конус биіктігі  -ның
-ның 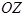 өсін айнала қозғалысының бұрыштық жылдамдығы.
өсін айнала қозғалысының бұрыштық жылдамдығы.
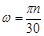 ,
,  теңдіктерін ескере отырып мына теңдікті аламыз:
теңдіктерін ескере отырып мына теңдікті аламыз:
 .
.
Конусқа түсірілген сыртқы күштер: салмақ күші  , жазықтықтың нормаль реакциясы
, жазықтықтың нормаль реакциясы  және үйкеліс күші
және үйкеліс күші  .
.  және
және  күштері
күштері  өсіне параллель, ал
өсіне параллель, ал  күшінің әсер ету сызығы жазықтықта жатыр.
күшінің әсер ету сызығы жазықтықта жатыр.
Массалар центрінің қозғалысы туралы теореманы пайдаланып, мынадай векторлық теңдеуді құрамыз:
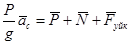 .
.
Теңдіктің екі жағын координаттар өстеріне проекциялаймыз:
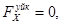


Осыдан: 
 .
.
 ал
ал  болғандықтан үйкеліс күші
болғандықтан үйкеліс күші  жасаушы бойымен
жасаушы бойымен  төбесіне қарай бағытталады.
төбесіне қарай бағытталады.
 1-мысал. Паром палубасындағы жүк жүкшығыр бойымен тұмсығынан құйрығына қарай қозғалады (15.2-сурет). Жүктің және паромның салмақтары
1-мысал. Паром палубасындағы жүк жүкшығыр бойымен тұмсығынан құйрығына қарай қозғалады (15.2-сурет). Жүктің және паромның салмақтары  және
және  . Егер жүк палубаның бойымен
. Егер жүк палубаның бойымен  аралыққа орын ауыстыратын болса, онда паром қандай аралыққа орын ауыстырады?
аралыққа орын ауыстыратын болса, онда паром қандай аралыққа орын ауыстырады?
Шешуі. Паром және жүкті бір жүйе ретінде қарастырамыз. Бұл жүйеге келесі сыртқы күштер түсірілген: паромның салмағы  , жүктің салмағы
, жүктің салмағы  және гидростатикалық су қысымы
және гидростатикалық су қысымы  . Барлық сыртқы күштердің горизонталь
. Барлық сыртқы күштердің горизонталь 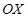 өсіне проекциялары нөлге тең болғандықтан, массалар центрі жылдамдығының сақталу заңы бойынша:
өсіне проекциялары нөлге тең болғандықтан, массалар центрі жылдамдығының сақталу заңы бойынша:
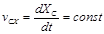 .
.
Бастапқы уақыт мезгілінде жүйе тыныштықта болады, сондықтан:  .
.
Осыдан:  .
.
Яғни, қарастырып отырған жүйенің массалар центрі өзінің орнын өзгеріссіз сақтайды. Координаттың бас нүктесі ретінде жүйе қозғалып бастағанға дейінгі паромның құйрығындағынүкте О-ны қабылдаймыз. Онда, жүйенің бастапқы және соңғы орын ауыстыруларының массалар центрі асциссалары үшін келесі теңдіктер сәйкес келеді:
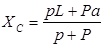 ,
,  ,
,
мұндағы,  паромның ұзындығы;
паромның ұзындығы;  паромның ауырлық центрінен, құйрығы арқылы жүргізілген вертикаль түзуге дейінгі ара қашықтық;
паромның ауырлық центрінен, құйрығы арқылы жүргізілген вертикаль түзуге дейінгі ара қашықтық;  анықталатын паромның орын ауыстыру аралығы.
анықталатын паромның орын ауыстыру аралығы.
Алдыңғы теңдіктердің оң жақтарын теңестіреміз:
 .
.
Осыдан: 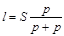 .
.
Орын ауыстыру 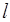 шамасы паромның өлшеміне және ауырлық центрінің орнына байланыссыз екенін көреміз.
шамасы паромның өлшеміне және ауырлық центрінің орнына байланыссыз екенін көреміз.
Сұрақ. Паром қайсы бағытта қозғалады?
Жауап.  0 болғандықтан паром оңға орын ауыстырады (15.2-сурет). Егер
0 болғандықтан паром оңға орын ауыстырады (15.2-сурет). Егер  <0 болса, онда паром қарама-қарсы бағытта қозғалған болар еді.
<0 болса, онда паром қарама-қарсы бағытта қозғалған болар еді.
15.4. Материалдық нүкте мен механикалық жүйенің қозғалыс мөлшері. Күштің элементар және толық импульсі.
 1. Материялық нүктенің қозғалыс мөлшері. Анықтама. Материялық нүктенің m массасы мен
1. Материялық нүктенің қозғалыс мөлшері. Анықтама. Материялық нүктенің m массасы мен  жылдамдығының көбейтіндісіне тең
жылдамдығының көбейтіндісіне тең  =m
=m  векторын оның қозғалыс мөлшері деп атаймыз.
векторын оның қозғалыс мөлшері деп атаймыз.  -векторы нүктеге түсірілген
-векторы нүктеге түсірілген  - күші әсерінен уақыт өткен сайын өзгеріп отырады (15.3-сурет).
- күші әсерінен уақыт өткен сайын өзгеріп отырады (15.3-сурет).
 dt көбейтіндісін күштің элементар импульсі деп атайды
dt көбейтіндісін күштің элементар импульсі деп атайды
Анықтама. Элементар импульстерден t = to уақыт аралығында алынған интегралмен анықталатын  векторын күштің сол уақыт аралығындағы импульсі деп атайды:
векторын күштің сол уақыт аралығындағы импульсі деп атайды:
 . (15.11)
. (15.11)
 2. Механикалық жүйенің қозғалыс мөлшері. Берілген механикалық жүйе n материялық нүктелерден құралады. Жүйенің массасы
2. Механикалық жүйенің қозғалыс мөлшері. Берілген механикалық жүйе n материялық нүктелерден құралады. Жүйенің массасы 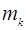 және жылдамдығы
және жылдамдығы  тең
тең  нүктесінің қозғалыс мөлшері
нүктесінің қозғалыс мөлшері 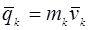 векторымен беріледі (15.4-сурет). Жүйедегі нүктелер қозғалыс мөлшері
векторымен беріледі (15.4-сурет). Жүйедегі нүктелер қозғалыс мөлшері  векторларының бас векторы механикалық жүйенің қозғалыс мөлшері ретінде алынады.
векторларының бас векторы механикалық жүйенің қозғалыс мөлшері ретінде алынады.
Басқаша айтқанда, механи-калық жүйенің қозғалыс мөлшері деп, ондағы барлық материялық нүктелердің қозғалыс мөлшерлерінің геометриялық қосындысына тең болатын  векторын айтамыз:
векторын айтамыз:
 . (15.12)
. (15.12)
 векторының координаттар өстеріндегі проекцияларын (15.12) –векторлық теңдікті сәйкес өстерге проекциялау арқылы табамыз:
векторының координаттар өстеріндегі проекцияларын (15.12) –векторлық теңдікті сәйкес өстерге проекциялау арқылы табамыз:


 . (15.13)
. (15.13)
Жүйенің қозғалыс мөлшері мен массалар центрінің жылдамдығы арасында тәуелділік бар. Оны табу үшін жүйе массаларының центрін анықтайтын қатынастың екі жағынан да уақыт бойынша туынды табамыз:
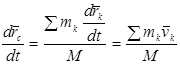 .
.
Осы теңдіктен мынау шығады: 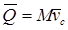 . (15.14)
. (15.14)
15.5. Материалық нүктенің және механикалық жүйенің қозғалыс мөлшерінің өзгеруі туралы теорема.
1. Материялық нүктенің қозғалыс мөлшерінің өзгеруі туралы теорема.
Нүкте динамикасының үш жалпы теоремасы бар. Олардың бәрі де осындағы негізгі заңнан қорытылып шығарылады. Осы теоремаларға тоқталайық.
Бұл вектордың бір уақыт ішіндегі өзгерісінің әсер етуші күшпен қандай байланыста болатындығын табайық. Ол үшін негізгі теңдеуді түрлендіреміз:
 , немесе
, немесе  . (15.15)
. (15.15)
Бұл теңдеудің екі жағын да dt-ға көбейтеміз:
 . (15.16)
. (15.16)
Теорема 1 материялық нүктенің қозғалыс мөлшерінің дифференциалы күшінің элементар импульсіне тең.
(15.16)-теңдеудің оң жағындағы Уақыт t = to болғанда нүкте жылдамдығы  =
= 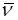 0 болады дейік. (15.16)-теңдіктің сол жағынан
0 болады дейік. (15.16)-теңдіктің сол жағынан  0-ден
0-ден  -ға дейінгі шектерде, ал оң жағынан t0-ден t-ға дейінгі шектердегі интегралдар алайық:
-ға дейінгі шектерде, ал оң жағынан t0-ден t-ға дейінгі шектердегі интегралдар алайық:
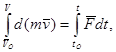
 . (15.17)
. (15.17)
Күш импульсінің координаттар өстеріндегі проекциялары мынадай теңдіктермен анықталынады: 
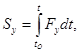
 . (15.18)
. (15.18)
(15.18) күштің толық импульсі, (15.17) келесі түрде жазылады:
 . (15.19)
. (15.19)
Теорема 2 . Қандай да уақыт аралығындағы нүктенің қозғалыс мөлшерлерінің өзгеруі сол уақыт аралығындағы күш импульсіне тең (15.18) және (15.19).
Векторлық теңдеу (15.19)-ді координаттық өстерге проекциялары:


 . (15.20)
. (15.20)
Күш импульсінің координаттық өстердегі проекцияларының (15.18) теңдеулерінде көрсетілген анықтамаларын пайдалансақ, онда соңғы скалярлық теңдеулерді мына түрде жазамыз:
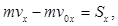

 . (15.20’)
. (15.20’)
Теореманың координаттық өстерге проекциясы былай айтылады: нүктенің қозғалыс мөлшерінің берілген өстегі проекциясының қандайда бір уақыт аралығындағы өзгеруі сол уақыт аралығындағы күш импульсінің осы өстегі проекциясына тең.
 2-мысал. Материялық нүкте М шеңбер бойымен бірқалыпты қозғалады (15.5-сурет). Нүктенің массасы
2-мысал. Материялық нүкте М шеңбер бойымен бірқалыпты қозғалады (15.5-сурет). Нүктенің массасы  және оның жылдамдығы
және оның жылдамдығы  .
.
Нүкте жарты шеңбер жол жүріп,  орнынан
орнынан  орнына орын ауыстырған уақыт аралығындағы нүктеге түсірілген күштің
орнына орын ауыстырған уақыт аралығындағы нүктеге түсірілген күштің  импульсін анықтау керек.
импульсін анықтау керек.
Шешуі. Материялық нүктенің қозғалыс мөлшерінің өзгеруі туралы теореманы пайдаланамыз:  ,
,
мұндағы, 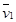 және
және  сәйкес
сәйкес  және
және  нүктелерінің жылдамдық векторлары.
нүктелерінің жылдамдық векторлары.
Есептің берілгені бойынша  , яғни:
, яғни:  , импульс
, импульс 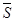 -тің бағыты
-тің бағыты  -нің бағытымен бағыттас, ал оның шамасы:
-нің бағытымен бағыттас, ал оның шамасы:
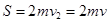 .
.
2. Механикалық жүйенің қозғалыс мөлшерінің өзгеруі туралы теорема. Жүйенің қозғалысы кезінде оның  қозғалысы мөлшері күштердің әсерінен уақыт өткен сайын өзгеріп отырады.
қозғалысы мөлшері күштердің әсерінен уақыт өткен сайын өзгеріп отырады.  векторы өзгеруінің жүйеге әсер етуші күштерге тәуелділігі мынадай теоремамен анықталады:
векторы өзгеруінің жүйеге әсер етуші күштерге тәуелділігі мынадай теоремамен анықталады:
Теорема 3. Механикалық жүйенің қозғалыс мөлшерінен уақыт бойынша алынған туынды жүйеге әсер етуші барлық сыртқы күштердің бас векторына тең.
Бұл теореманы дәлелдеу үшін механикалық жүйе қозғалысының дифференциалдық теңдеулерін еске түсірейік:

 .
.
Осы теңдеулердің барлығын бір-біріне қосайық, сонда алатынымыз:
 . (15.21)
. (15.21)
Бұл теңдіктің оң жағындағы қосындылардың екіншісі, ішкі күштер қосындысы, нөлге тең. Ал оның сол жағындағы қосынды  векторынан уақыт бойынша алынған туындыға тең:
векторынан уақыт бойынша алынған туындыға тең:
 . (15.22)
. (15.22)
Сондықтан (15.21) –теңдеуден іздеп отырған теореманың өрнегі мына түрге келеді:
 немесе
немесе  . (15.23)
. (15.23)
Осымен, жоғарыда айтылған теорема дәлелденді (15.23) теңдігі жүйенің қозғалыс мөлшерінің өзгеруі туралы теореманың дифференциалдық өрнегін береді. Векторлық теңдеу (15.23) декарттық координаттар өстеріне проекциялаудан 3 скаляр теңдеу аламыз:
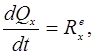

 . (15.24)
. (15.24)
(15.24) – теңдеулер, механикалық жүйенің қозғалыс мөлшерінің координаттық өстердегі проекцияларынан уақыт бойынша алынған туындылары жүйенің сыртқы күштерінің бас векторының сол өстердегі проекцияларына тең болатындығын көрсетеді.
Қозғалыс мөлшерінің өзгеруі туралы теореманың дифференциалдық теңдеуінің интегралдық өрнегі:
 .
.
Бұдан:  , (15.25)
, (15.25)
мұндағы,  -
-  уақытқа, ал
уақытқа, ал  уақытқа сәйкес келетін жүйенің қозғалыс мөлшері
уақытқа сәйкес келетін жүйенің қозғалыс мөлшері  векторының мәндері. (15.25) теңдігіндегі интеграл сыртқы күштердің бас векторы
векторының мәндері. (15.25) теңдігіндегі интеграл сыртқы күштердің бас векторы  -нің
-нің  уақыт аралығындағы импульсі деп аталады. Оны
уақыт аралығындағы импульсі деп аталады. Оны 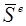 деп белгілейік, сонда алатынымыз:
деп белгілейік, сонда алатынымыз:
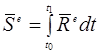 . (15.26)
. (15.26)
Бұл анықтаманы әрбір жеке  сыртқы күштердің импульстері арқылы да өрнектей аламыз:
сыртқы күштердің импульстері арқылы да өрнектей аламыз:
 .
.
Оң жақтағы қосындының белгісі ішіндегі интегралды жүйенің  -шы нүктесіне әсер ететін,
-шы нүктесіне әсер ететін, 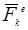 сыртқы күшінің
сыртқы күшінің  уақыт аралығындағы импульсі деп атаймыз:
уақыт аралығындағы импульсі деп атаймыз:
 .
.
Бұл теңдікті ескере отырып, (4.21) – анықтаманы мына түрде жазуға болады:
 . (15.27)
. (15.27)
(15.27) теңдігі сыртқы күштердің бас векторының қандай да бір уақыт аралығындағы импульсі (15.26) жүйеге әсер етуші сыртқы күштердің сол уақыт аралығындағы барлық импульстерінің геометриялық қосындысына тең екендігін көрсетеді. Егер күштер импульсінің анықтамасы болып табылатын (15.26) немесе (15.27) теңдіктерін пайдалансақ, онда (15.25) – теореманы былай жазамыз:
 немесе
немесе  . (15.28)
. (15.28)
(15.25) немесе (15.28) жүйенің қозғалыс мөлшерінің өзгеруі туралы теореманы береді. Теорема 4. Жүйенің қозғалыс мөлшерінің қандай да бір уақыт аралығындағы өзгеруі, сыртқы күштердің бас векторының сол уақыт аралығындағы импульсіне тең. (15.28) векторлық үш скаляр теңдеуге эквивалентті:


 , (15.29)
, (15.29)
немесе: 
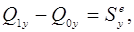
 . (15.30)
. (15.30)
Сақталу заңы. Егер механикалық жүйеге әсер ететін сыртқы күштерінің бас векторы нөлге тең болып келетін болса 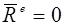 , онда теорема өрнегі (15.25) теңдеуінен мынадай теңдік шығады:
, онда теорема өрнегі (15.25) теңдеуінен мынадай теңдік шығады:
 , (15.31)
, (15.31)
мұндағы,  жүйенің қозғалыс мөлшерінің бастапқы мәні. (15.31) –теңдік қозғалыс мөлшерінің сақталу заңының теоремасын береді.
жүйенің қозғалыс мөлшерінің бастапқы мәні. (15.31) –теңдік қозғалыс мөлшерінің сақталу заңының теоремасын береді.
Теорема 5. Егер сыртқы күштердің бас векторы  болып келсе, онда механикалық жүйенің
болып келсе, онда механикалық жүйенің  векторы қозғалыс кезінде өзінің шамасы мен бағытын өзгертпей сақтайды.
векторы қозғалыс кезінде өзінің шамасы мен бағытын өзгертпей сақтайды.
 3-мысал. Вертикаль жазықтыққа қатысты симметриялы
3-мысал. Вертикаль жазықтыққа қатысты симметриялы  каналымен сұйық
каналымен сұйық  жылдамдықпен ағады (15.6-сурет).
жылдамдықпен ағады (15.6-сурет).
Каналдың көлденең қимасы тұрақты және 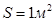 -қа тең. Сұйықтың түйіршігінің жылдамдық векторы каналға кірерде горизонтпен
-қа тең. Сұйықтың түйіршігінің жылдамдық векторы каналға кірерде горизонтпен  , ал каналдан шығарда горизонтпен
, ал каналдан шығарда горизонтпен  бұрыш жасайды.
бұрыш жасайды.
Сұйықтың канал қабырғасына түсіретін қысым күшінің горизонталь құраушысын анықтау керек.
Шешуі. Мәселені шешу үшін, жүйенің қозғалыс мөлшерінің өзгеруі туралы теореманы пайдаланамыз. Механикалық жүйе ретінде каналдың қабырғаларымен, 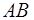 және
және  қималарымен шектелген,
қималарымен шектелген,  уақыт сәтіндегі көлемді толтыратын сұйық түйіршіктерінің жүйесін қарастырамыз.
уақыт сәтіндегі көлемді толтыратын сұйық түйіршіктерінің жүйесін қарастырамыз.
Қандай да  уақыт аралығында сұйық түйіршіктері орын ауыстырады және
уақыт аралығында сұйық түйіршіктері орын ауыстырады және 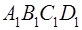 көлемді толтырады. Механикалық жүйенің қозғалыс мөлшері
көлемді толтырады. Механикалық жүйенің қозғалыс мөлшері  уақыт мезгілінде
уақыт мезгілінде 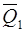 , ал
, ал  уақыт мезгілінде
уақыт мезгілінде  болады. Айырмасы:
болады. Айырмасы: 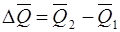 ,
,
 уақыт аралығындағы жүйе қозғалыс мөлшерінің өсімшесіне тең.
уақыт аралығындағы жүйе қозғалыс мөлшерінің өсімшесіне тең.
Қозғалыс мөлшері 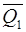 ,
,  және
және  көлемдерді толты-ратын сұйық түйіршіктерінің
көлемдерді толты-ратын сұйық түйіршіктерінің  және
және  қозғалыс мөлшерінің қосындысына тең, яғни:
қозғалыс мөлшерінің қосындысына тең, яғни:
 .
.
Дәл осы сияқты, 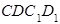 көлемді толтыратын сұйық түйіршіктерінің қозғалыс мөлшерін
көлемді толтыратын сұйық түйіршіктерінің қозғалыс мөлшерін  деп белгілейміз, онда:
деп белгілейміз, онда:  .
.
Сұйықтың каналмен біркелкі қозғалысында  уақыт аралығында қозғалыс мөлшері
уақыт аралығында қозғалыс мөлшері  өзгермейді:
өзгермейді:  , немесе:
, немесе: 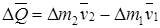
 (
( 
мұндағы,  және
және  сұйық түйіршіктерінің
сұйық түйіршіктерінің 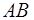 және
және  қимала-рындағы сәйкес жылдамдықтары;
қимала-рындағы сәйкес жылдамдықтары;  және
және  -
-  және
және 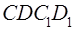 көлемдердегі сұйықтың массалары.
көлемдердегі сұйықтың массалары.
Есептің берілгені бойынша каналдың көлденең қималары тұрақты, сондықтан:
 .
.
Сұйықтың тығыздығын  , ал
, ал  уақыт аралығында сұйық түйіршіктерінің орын ауыстыруын
уақыт аралығында сұйық түйіршіктерінің орын ауыстыруын  деп белгілейміз.
деп белгілейміз.
Каналдың кез келген екі қимасы арқылы бір уақыт мезгілінде бірдей сұйық ағып өтеді, сондықтан:  .
.
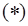 теңдігін горизонталь
теңдігін горизонталь  өсіне проекциялаймыз:
өсіне проекциялаймыз:
 .
.
Теңдіктің екі жағын  -ға бөліп, туындының анықтамасын пайдалансақ, алатынымыз:
-ға бөліп, туындының анықтамасын пайдалансақ, алатынымыз:
 . (
. ( 
Теорема бойынша:
 ,
, 
мұндағы,  жүйеге түсірілген сыртқы күштердің негізгі векторы-ның
жүйеге түсірілген сыртқы күштердің негізгі векторы-ның 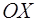 өсіне проекциясы.
өсіне проекциясы.
 және
және  теңдіктерінің оң жақтарын теңестіру арқылы алатынымыз:
теңдіктерінің оң жақтарын теңестіру арқылы алатынымыз:
 .
.
Судың тығыздығы  . Онда:
. Онда:  .
.
4-мысал. Массалары  және
және  екі шар горизонталь жазықтықтың бетінде дөңгелеп қозғалады (15.7-сурет). Шарлар біртекті және олардың диаметрлері тең. Шарлардың жылдамдықтары
екі шар горизонталь жазықтықтың бетінде дөңгелеп қозғалады (15.7-сурет). Шарлар біртекті және олардың диаметрлері тең. Шарлардың жылдамдықтары  және
және  .
.
 Шарлардың соқтығысынан соң 1-шар центрінің жылдамдығы
Шарлардың соқтығысынан соң 1-шар центрінің жылдамдығы  -ке тең болады, ал оның бағыты өзгермейді.
-ке тең болады, ал оның бағыты өзгермейді.
Соқтығыстан соң  -шар центрі қандай жылдамдықпен қозғала-тынын анықтау керек. Шарлар мен жазықтықтың арасындағы үйкеліс есепке алынбайды.
-шар центрі қандай жылдамдықпен қозғала-тынын анықтау керек. Шарлар мен жазықтықтың арасындағы үйкеліс есепке алынбайды.
Шешуі. Шарларды жүйе ретінде қарастырамыз. Бұл жүйе үшін, соқтығыс кезіндегі шарлардың өзара әсер күштері ішкі күштер болады. Сыртқы күштердің  өсіне проекциялары нөлге тең, яғни жүйенің қозғалыс мөлшерінің сақталу заңы бойынша:
өсіне проекциялары нөлге тең, яғни жүйенің қозғалыс мөлшерінің сақталу заңы бойынша:
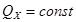 немесе
немесе  ,
,
мұндағы, 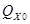 және
және  соқтығысқа дейінгі және соқтығыстан кейінгі жүйе қозғалыс мөлшерінің
соқтығысқа дейінгі және соқтығыстан кейінгі жүйе қозғалыс мөлшерінің 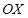 өсіне проекциялары.
өсіне проекциялары.
 және
және  -шарлар центрлерінің жылдамдықтарын
-шарлар центрлерінің жылдамдықтарын  және
және  деп белгілейміз. Сонда:
деп белгілейміз. Сонда:
 ,
,
 .
.
 және
және  теңдіктерін ескере отырып, алдыңғы
теңдіктерін ескере отырып, алдыңғы
екі теңдіктің екі жағын теңестіреміз:
 .
.
Осыдан:
 ,
,
 болғандықтан
болғандықтан  -шар қозғалысының бағыты өзгермейді.
-шар қозғалысының бағыты өзгермейді.
15.6. Нүктеге және өске қатысты материялық нүктенің қозғалыс мөлшерінің моменті
Материялық нүктенің қозғалыс мөлшерінің қандайда бір центрге қатысты алынған моментін оның сол центрге қатысты қозғалыс мөлшері моменті деп атайды.
 О центріне қатысты алынған кинетикалық моментін
О центріне қатысты алынған кинетикалық моментін  0 әрпімен белгілейік. Сонда ол
0 әрпімен белгілейік. Сонда ол  0 =
0 =  немесе
немесе  түріндегі өрнекпен беріледі.
түріндегі өрнекпен беріледі.
Ескерту: қозғалыс мөлшері моменті және кинетикалық момент екеуі бір ұғым.
15.7. Механикалық жүйенің нүктеге және оське қатысты қозғалыс мөлшері моментінің бас векторы
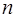 материялық нүктеден тұратын механикалық жүйе қозғалысын OXYZ инерциялық өстер жүйесіне қатысты қарастырайық (15.8-сурет). Жүйедегі әрбір нүктенің козғалыс мөлшері:
материялық нүктеден тұратын механикалық жүйе қозғалысын OXYZ инерциялық өстер жүйесіне қатысты қарастырайық (15.8-сурет). Жүйедегі әрбір нүктенің козғалыс мөлшері:
 . (15.32)
. (15.32)
және оның О центріне қатысты алынған кинетикалық моменті:
 (15.33)
(15.33)
 векторы О нүктесінде
векторы О нүктесінде  және
және  -векторларының жазықтығына перпендикуляр бағытталады.
-векторларының жазықтығына перпендикуляр бағытталады.  векторларының бас векторын алайық.
векторларының бас векторын алайық.
Анықтама. Жүйе нүктелерінің О центрге қатысты алынған кинетикалық моменттерінің бас векторын (геометриялық қосындысын) сол О центріне қатысты алынған механикалық жүйенің қозғалыс мөлшер моменті деп атаймыз. Жүйенің О центріне қатысты қозғалыс мөлшер моментін  деп белгілесек, онда ол анықтама бойынша мынаны аламыз:
деп белгілесек, онда ол анықтама бойынша мынаны аламыз:
 , (15.34)
, (15.34)
немесе (15.33) теңдігін ескерсек шығатыны:
 . (15.35)
. (15.35)
векторының бас нүктесі О центрінде жатады. Қозғалыс мөлшер моменті механикалық жүйенің айнала қозғалысын сипаттайды.
Жүйенің  кинетикалық моментін OXYZ координаттық өстерге проекциялайық:
кинетикалық моментін OXYZ координаттық өстерге проекциялайық:
 (15.36)
(15.36)
Проекциялары (3.87) теңдіктерімен анықталатын векторының модулі мынадай:
 . (15.37)
. (15.37)
Оның бағыттаушы косинустары:


 (15.38)
(15.38)
15.8. Материялық нүктенің және механикалық жүйенің қозғалыс мөлшері моментінің өзгеру туралы теорема
 1. Материялық нүктенің қозғалыс мөлшері моментінің өзгеруі туралы теоремасы
1. Материялық нүктенің қозғалыс мөлшері моментінің өзгеруі туралы теоремасы
Қозғалыс мөлшер моменті (кинетикалық момент) күш әсерінен уақыт өткен сайын өзгеріп тұрады (15.9 -сурет).
Оның өзгерісінің күшке тәуелділігін табайық. Ол үшін негізгі теңдеудің екі жағын да нүктенің  радиус-векторына векторлық түрде көбейтейік:
радиус-векторына векторлық түрде көбейтейік:
 . (15.39)
. (15.39)
Бұл теңдеудің сол жағындағы векторлық көбейтіндіні түрлендірейік:
 . (15.40)
. (15.40)
Бұл арада азайтқыш векторлық көбейтіндінің нөлге айналатынын ескердік. Ол екі коллинеарлық вектордың векторлық көбейтіндісі болуы себепті нөлге айналады. (15.39) - теңдіктің сол жағындағы векторлық көбейтіндіні (15.40) түрінде аламыз:
 . (15.41)
. (15.41)
Осы теңдік материялық нүкте қозғалыс мөлшері моментінің өзгеруі туралы немесе басқаша айтқанда, нүктенің кинетикалық моментінің өзгеруі туралы теореманы өрнектейді. Жоғарыда берілген материялық нүктенің кинетикалық моменті деген анықтаманы қолдану арқылы (15.41) теңдігін басқа түрде де жазуға болады:
 . (15.42)
. (15.42)
(15.41) не (15.42) теңдігімен өрнектелетін теореманы сипаттайды
Теорема 6. Қандай да бір центрге қатысты алынған нүкте кинетикалық моментінің уақыт бойынша туындысы сол центрге қатысты күш моментіне тең.
(15.42)-теңдеуді координаттық үш өске проекциялап жазайық:


 . (15.43)
. (15.43)
(15.36)-теңдіктері нүктенің координаттар өстеріне қатысты алынған кинетикалық моменттерінің өзгеруін сипаттайды:
Теорема 7. Координаттар өстеріне қатысты алынған нүкте кинетикалық моменттерінің уақыт бойынша туындылары сол өстерге қатысты алынған күш моменттеріне тең.
 5-мысал. Жердің айналасында спутник эллипс траекториясын сыза қозғалады. Эллипстің бір фокусында жердің центрі орналасқан. Спутниктің жерге жақын нүктесіндегі уақыт мезгілінде жылдамдығы
5-мысал. Жердің айналасында спутник эллипс траекториясын сыза қозғалады. Эллипстің бір фокусында жердің центрі орналасқан. Спутниктің жерге жақын нүктесіндегі уақыт мезгілінде жылдамдығы  -ға тең (15.10-сурет).
-ға тең (15.10-сурет).
Спутниктің жерден ең алыс нүктесіндегі 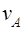 жылдамдығын анықтау керек.
жылдамдығын анықтау керек.
Шешуі. Спутникке әсер ететін  күші бүкіл әлемдік тартылыс күші болғандықтан, әсер ету сызығы жердің центріне бағытталады.
күші бүкіл әлемдік тартылыс күші болғандықтан, әсер ету сызығы жердің центріне бағытталады.
Сондықтан, жердің центріне қатысты спутниктің қозғалыс мөлшерінің моменті тұрақты болады. Яғни, спутниктің  және
және 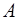 нүктелеріндегі қозғалыс мөлшерлерінің моменттері өзара тең:
нүктелеріндегі қозғалыс мөлшерлерінің моменттері өзара тең:
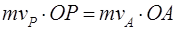 , мұндағы,
, мұндағы, 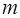 -спутниктің массасы;
-спутниктің массасы;
 -жердің центрі О-дан перигей Р-ға дейінгі ара қашықтық;
-жердің центрі О-дан перигей Р-ға дейінгі ара қашықтық;
 -жердің центрі О-дан апогей А-ға дейінгі ара қашықтық.
-жердің центрі О-дан апогей А-ға дейінгі ара қашықтық.
Осыдан:  .
.
Перигейде спутниктің жылдамдығы ең кіші шамаға, ал апогейде ең үлкен шамаға тең.
2. Механикалық жүйенің қозғалыс мөлшері моментінің өзгеруі туралы теорема
Теорема 8. Қандай да бір қозғалмайтын центрге қатысты алынған механикалық жүйенің кинетикалық моментінің уақыт бойынша алынған туындысы сол центрге қатысты алынған жүйедегі сыртқы күштердің бас моментіне тең.
Теореманы дәлелдеу мақсатымен берілген механикалық жүйенің қандай да бір нүктесін  алайық та, оған әсер ететін сыртқы
алайық та, оған әсер ететін сыртқы  және ішкі
және ішкі  күштерді ескере отырып оның қозғалысының дифференциалдық теңдеуін құрайық:
күштерді ескере отырып оның қозғалысының дифференциалдық теңдеуін құрайық:
 . (15.44)
. (15.44)
Мұндай теңдеулерді әрбір нүкте үшін құруға болатындықтан олардың жалпы саны  жүйедегі нүктелер санына тең болады. Осы (15.44) – тегі
жүйедегі нүктелер санына тең болады. Осы (15.44) – тегі  теңдеудің әрқайсысын сәйкес нүктелердің радиус-векторлары
теңдеудің әрқайсысын сәйкес нүктелердің радиус-векторлары  -ге векторлық түрде көбейтіп, оларды бір-біріне қосамыз:
-ге векторлық түрде көбейтіп, оларды бір-біріне қосамыз:
 . (15.45)
. (15.45)
(3.91)-теңдіктің сол жағындағы қосындыны түрлендіреміз:
 . (15.46)
. (15.46)
Жүйенің ішкі күштерінің қасиеті бойынша ішкі күштердің бас моменті әр уақытта нөлге тең болады. Сондықтан да (15.46)-теңдіктің оң жағындағы екінші қосындысы нөлге тең:
 . (15.47)
. (15.47)
(15.46) және (15.47) теңдіктерін пайдалана отырып (15.45)-теңдігін мына түрге келтіреміз:
 . (15.48)
. (15.48)
Егер (15.48) теңдігінің сол жағындағы қосынды жүйенің кинетикалық моменті  -ге, ал оның оң жағындағы қосынды сыртқы күштердің О центріне қатысты алғандағы бас моменті
-ге, ал оның оң жағындағы қосынды сыртқы күштердің О центріне қатысты алғандағы бас моменті 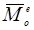 векторына тең екенін ескерсек, онда бұл теңдікті мына түрде ықшамдап жазуға болады:
векторына тең екенін ескерсек, онда бұл теңдікті мына түрде ықшамдап жазуға болады:
 . (15.49)
. (15.49)
Осымен теорема дәлелденді. Теорема (15.48) немесе (15.31) түріндегі бір векторлық теңдікпен беріледі.
Жоғарыдағы тағайындалған (15.30) және (15.49) векторлық теңдіктерді координаттық түрге келтірейік. Ол үшін кинетикалық моментті және күштер бас моментін үш құраушыға жіктейміз.
 және
және  . (15.50)
. (15.50)
Енді (15.50) теңдіктеріне сүйене отырып (15.49) векторлық теңдікті мынадай үш скаляр теңдіктерімен алмастыра аламыз:


 . (15.51)
. (15.51)
3. Сақталу заңы. Егер О нүктесіне қатысты алынған сыртқы күштер бас моменті  болса, онда жүйенің сол нүктеге қатысты алынған қозғалыс мөлшері моментінің шамасы да, бағыты да өзгермейді, тұрақты қалпында қалады.
болса, онда жүйенің сол нүктеге қатысты алынған қозғалыс мөлшері моментінің шамасы да, бағыты да өзгермейді, тұрақты қалпында қалады.

 . (15.52)
. (15.52)
Бұл (15.52) теңдігі О центріне қатысты алынған қозғалыс мөлшері моменттің сақталу заңын сипаттайды.
Егер сыртқы күштердің О центріне қатысты алғандағы бас моменті нөлге тең болса, онда оның осы центрден өтетін координаттар өстеріндегі проекциялары да нөлге тең болады: 

 .
.
Сол себепті (15.51)-теңдіктерінен алатынымыз:

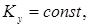
 . (15.53)
. (15.53)
15.9 Материялық нүктенің және механикалық жүйенің кинетикалық энергиясы. Анықтама. Нүктенің кинетикалық энергиясы деп оның массасы мен жылдамдығының квадратының көбейтіндісінің жартысына тең болатын скаляр шаманы айтады. Нүктенің кинетикалық энергиясы:
 . (15.54)
. (15.54)
Күш әсерінен нүктенің жылдамдығы  өзгерді. Сол себепті кинетикалық энергия да уақыт өткен сайын өзгеріп отырады.
өзгерді. Сол себепті кинетикалық энергия да уақыт өткен сайын өзгеріп отырады.
Анықтама. Механикалық жүйенің кинетикалық энергиясы деп ондағы барлық материялық нүктелердің кинетикалық энергияларының қосындысына тең скаляр шаманы айтамыз.
Массасы  әрбір материялық нүктенің кинетикалық энергиясы:
әрбір материялық нүктенің кинетикалық энергиясы:

 (15.55)
(15.55)
Онда, анықтама бойынша, n материялық нүктеден тұратын механикалық жүйенің кинетикалық энергиясы осылардын арифметикалық қосындысына тең:
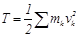 , (15.56)
, (15.56)
немесе:
 . (15.57)
. (15.57)
Кинетикалық энергия қозғалыс мөлшерімен қатарлас келетін жүйе қозғалысының негізгі екі өлшемінің бірі болып табылады. Жоғарыда айтқанымыздай, жүйенің қозғалыс мөлшері оның ілгерілемелі қозғалысын сипаттайды. Ал кинетикалық энергия механикалық қозғалысты толық көлемінде тереңірек сипаттайды.
Өзгермейтін механикалық жүйенің (абсолют катты дене) қозғалысы үшін (15.55) өрнегін қолдануға ыңғайлы түрге келтіруге болады.
15.10. Қатты дененің ілгерілмелі, айналмалы және жазықпараллель қозғалыстағы кинетикалық энергиясы
1. Ілгерілемелі қозғалыстағы катты дененің кинетикалық энергиясы
Ілгерілемелі қозғалыстағы дене нүктелерінің жылдамдықтары өзара тең болғандықтан (15.55) формуладағы жылдамдық квадратын ортақ көбейткіш ретінде қосынды белгісінің алдына шығады:
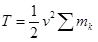 .
.
Дене нүктелерінің массаларының қосындысы  дене массасын береді. Олай болса ілгерілемелі қозғалыстағы қатты дене кинетикалық энергиясы:
дене массасын береді. Олай болса ілгерілемелі қозғалыстағы қатты дене кинетикалық энергиясы:
 . (15.58)
. (15.58)
Сонымен, ілгерілемелі қозғалыстағы қатты дененің кинетикалық энергиясы дененің массасы мен оның жылдамдығының квадратының көбейтіндісінің жартысына тең.
2. Қозғалмайтын өсті айнала қозғалатын қатты дененің кинетикалық энергиясы. Айналмалы қозғалыстағы дене нүктеле-рінің жылдамдықтары олардың айналу өсінен қашықтықтарына пропорционал болып келеді:  .
.
Осыларды (3.112) формуласына қойсақ алатынымыз:  .
.
Мұндағы,  ортақ қөбейткішті қосынды белгісінің алдына шығарсақ және дене нүктелерінің массалары мен олардың айналу өсінен қашықтықтарының квадраттары көбейтінділерінің қосындысы
ортақ қөбейткішті қосынды белгісінің алдына шығарсақ және дене нүктелерінің массалары мен олардың айналу өсінен қашықтықтарының квадраттары көбейтінділерінің қосындысы  – айналу өсіне қатысты алынған дененің инерция моментін анықтайтынын ескерсек, онда мынадай формула аламыз:
– айналу өсіне қатысты алынған дененің инерция моментін анықтайтынын ескерсек, онда мынадай формула аламыз:  . (15.59)
. (15.59)
Айналмалы қозғалыстағы қатты дененің кинетикалық энергиясы дененің айналу өсіне қатысты алынған инерция моменті мен оның бұрыштық жылдамдығының квадратына көбейтіндісінің жартысына тең.
3. Кенигтің теоремасы. Механикалық жүйенің күрделі қозғалы-сының кинетикалық энергиясын есептеуде Кенигтің теоремасы қолданылады. Механикалық жүйенің күрделі қозғалысын екі жәй қозғалысқа жіктеуге болады. Оның бірі – массалар центрінің қозғалысымен анықталатын ілгерілемелі қозғалыс, ал екіншісі жүйенің массалар центрі төңірегіндегі салыстырмалы қозғалысы. Осыған байланысты  нүктенің жылдамдығы да екі жылдамдық қосындысына тең болады:
нүктенің жылдамдығы да екі жылдамдық қосындысына тең болады:
 , (15.60)
, (15.60)
мұндағы,  – жүйенің массалары центрінің жылдамдығы,
– жүйенің массалары центрінің жылдамдығы,  – жүйе-мен бірге массалар центрі төңірегіндегі қозғалуынан туатын
– жүйе-мен бірге массалар центрі төңірегіндегі қозғалуынан туатын  нүк-тенің жылдамдығы. Бұл (3.116) формуламен анықталатын жылдамдықтарды (3.112) теңдігіне апарып қою арқылы мынадай нәтиже аламыз:
нүк-тенің жылдамдығы. Бұл (3.116) формуламен анықталатын жылдамдықтарды (3.112) теңдігіне апарып қою арқылы мынадай нәтиже аламыз:
 . (15.61)
. (15.61)
Бұл (3.117) -теңдігіндегі:
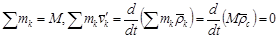 . (15.62)
. (15.62)
Мұндағы  , өйткені массалар центрі С –қозғалмалы
, өйткені массалар центрі С –қозғалмалы  координаттық өстер жүйесінің бас нүктесі. Осы (15.62) теңдіктерін еске ала отырып, (15.61) теңдігін ақырғы түрде былай жазамыз:
координаттық өстер жүйесінің бас нүктесі. Осы (15.62) теңдіктерін еске ала отырып, (15.61) теңдігін ақырғы түрде былай жазамыз:
 . (15.63)
. (15.63)
Соңғы қосынды механикалық жүйенің массалар центріне, яғни ілгерілемелі қозғалыстағы  -санақ жүйесіне қатысты алынғандағы салыстырмалы қозғалыстың кинетикалық энергиясы, сондықтан оны
-санақ жүйесіне қатысты алынғандағы салыстырмалы қозғалыстың кинетикалық энергиясы, сондықтан оны 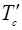 деп белгілейік, ол:
деп белгілейік, ол:
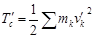 . (15.64)
. (15.64)
Сонда (15.63) теңдігін қысқаша мына түрде жазуға болады:
 . (15.65)
. (15.65)
Кенигтің теоремасы былай айтылады: күрделі қозғалыстағы механикалық жүйенің кинетикалық энергиясы массалар центрінің қозғалысымен анықталатын ілгерілемелі қозғалыстың кинетикалық энергиясына, жүйенің массалар центрінің төңірегінде орындалатын салыстырмалы қозғалысының кинетикалық энергиясын қосқаннан шығатын қосындыға тең.
4. Жазық-параллель қозғалыстағы қатты дененің кинетикалық энергиясы. Дененің жазық параллель қозғалысын массалар центрінің қозғалысымен анықтайтын ілгерілемелі қозғалыс пен массалар центрі төңірегіндегі, 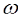 лездік бұрыштық жылдамдықпен орындалатын, лездік айналыстан тұрады деп есептеуге болады. Массалар центрі С арқылы өтетін және қозғалыс жазықтығына үнемі перпендикуляр болып келетін дененің лездік айналу өсін CZ деп белгілесек, онда (15.64) формуласы бойынша анықталатын
лездік бұрыштық жылдамдықпен орындалатын, лездік айналыстан тұрады деп есептеуге болады. Массалар центрі С арқылы өтетін және қозғалыс жазықтығына үнемі перпендикуляр болып келетін дененің лездік айналу өсін CZ деп белгілесек, онда (15.64) формуласы бойынша анықталатын 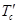 бұл жолы мынадай болады:
бұл жолы мынадай болады:
 . (15.66)
. (15.66)
 табылған мәнін (3.122) формуласындағы Кенигтің (15.65) теорема-сындағы орнына апарып қойсақ, жазық параллель қозғалыстағы қатты дененің кинетикалық энергиясын есептеуге қолданылатын формула аламыз:
табылған мәнін (3.122) формуласындағы Кенигтің (15.65) теорема-сындағы орнына апарып қойсақ, жазық параллель қозғалыстағы қатты дененің кинетикалық энергиясын есептеуге қолданылатын формула аламыз:
 . (15.67)
. (15.67)
5. Еркін қозғалыстағы қатты дененің кинетикалық энергиясы. Еркін қатты дененің массалар центрі жанында орындалатын қозғалыстары С нүктесінен өтетін лездік айналыстарға келтірілгендіктен  салыстырмалы қозғалыс энергиясы мынадай формула-мен анықталады:
салыстырмалы қозғалыс энергиясы мынадай формула-мен анықталады:
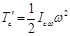 , (15.68)
, (15.68)
мұндағы  – массалар центрі С нүктесінен өтетін және
– массалар центрі С нүктесінен өтетін және  лездік бұрыштық жылдамдық векторымен бірдей бағытталатын лездік айналу өсіне қатысты алынған дененің инерция моменті. (15.67) теңдігін Кенигтің теоремасын өрнектейтін (15.63) формуладағы орнына қойсақ, онда мынаны аламыз:
лездік бұрыштық жылдамдық векторымен бірдей бағытталатын лездік айналу өсіне қатысты алынған дененің инерция моменті. (15.67) теңдігін Кенигтің теоремасын өрнектейтін (15.63) формуладағы орнына қойсақ, онда мынаны аламыз:
 . (15.69)
. (15.69)
Сонымен, еркін қозғалыстағы қатты дененің кинетикалық энергиясы (15.69) формуласымен анықталады. Жалпы алғанда, 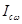 инерция моменті айнымалы шама болып келеді.
инерция моменті айнымалы шама болып келеді.
15.10.3. Күштің элементар және толық жұмысы. Күшінің d 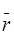 элементар орын ауыстыруға көбейтіндісін күштің элементар жұмысы деп атайды. Элементар жұмысты d’А деп белгілейміз:
элементар орын ауыстыруға көбейтіндісін күштің элементар жұмысы деп атайды. Элементар жұмысты d’А деп белгілейміз:
 , (15.70)
, (15.70)
векторлардың проекциялары арқылы жазылуы:
 . (15.71)
. (15.71)
Элементар жұмысты жолдың dS дифференциалы және күш  пен
пен  -ның нүкте жылдамдығы бағытының арасындағы α бұрышы арқылы да өрнектей аламыз (15.11-сурет):
-ның нүкте жылдамдығы бағытының арасындағы α бұрышы арқылы да өрнектей аламыз (15.11-сурет):  . (15.72)
. (15.72)
 Бұл формуладағы F және dS оң шамалар
Бұл формуладағы F және dS оң шамалар  элементар жұмыс-тың таңбасы cosα таңбасымен бірдей. Егер α сүйір болса,
элементар жұмыс-тың таңбасы cosα таңбасымен бірдей. Егер α сүйір болса,  оң, α доғал болса,
оң, α доғал болса,  теріс таңбалы болады.
теріс таңбалы болады.
Күштің элементар жұмысын есептеу үшін керекті тағы бір формуланы көрсетейік. Бұл арада d  =
=  dt екенін еске аламыз да, элементар жұмыс өрнегін жаңа түрге келтіреміз:
dt екенін еске аламыз да, элементар жұмыс өрнегін жаңа түрге келтіреміз:
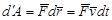 . (15.73)
. (15.73)
Элементар жұмыстың әр түрлі өрнегіне сәйкес, күштің толық жұмысы да әр түрлі формулалармен сипатталады:


 . (15.74)
. (15.74)
Жұмыс өлшемінің бірлігі үшін (БҚЖ) жүйесінде 1 Джоуль алынады (1ДЖ = 1Нм), ал техникалық жүйеде –1кГм (1кГм = 9,81ДЖ).
 жолындағы күштің толық жұмысы А қисықтың
жолындағы күштің толық жұмысы А қисықтың  доғасы бойындағы элементар жұмыстарынан алынған қисық сызықты интегралға тең:
доғасы бойындағы элементар жұмыстарынан алынған қисық сызықты интегралға тең:
 . (15.75)
. (15.75)
6-мысал. Салмағы 2т жүкті горизонтпен 30° бұрыш құратын көлбеу жазықтықтың бойымен 5м биіктікке көтеру үшін жұмсалатын ең аз жұмысты анықтау қажет. Үйкеліс коэффициенті 0.5-ке тең (15.12-сурет).
Шешуі. Жүкке түсірілген күштер: оның салмақ күші –  , үйкеліс күші –
, үйкеліс күші – 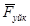 , көлбеу жазықтықтың нормаль реакция күші
, көлбеу жазықтықтың нормаль реакция күші  .
.
 x
x

s

h
a
O a 
15.12-сурет
Көлбеу жазықтыққа параллель, бас нүктесі қозғалыс басталатын нүкте болатын жоғары бағытта x өсін бағыттаймыз.
Жүкті жоғары көтеруге жұмсалатын жұмыс, түсірілген күштердің жұмыстарының қосындысына тең:

Салмақ күшінің жұмысы теріс шамаға тең, себебі жүк жер бетінен жоғары көтеріледі:  .
.
Үйкеліс күшінің жұмысын мынадай формула арқылы анықтаймыз:
 .
.
Егер жүк h=5м биіктікке көтерілетін болса  , онда:
, онда:
 .
.
Орын ауыстыру бағытына перпендикуляр болғандықтан нормаль реакция  -нің жұмысы нөлге тең, яғни
-нің жұмысы нөлге тең, яғни  .
.
Сонымен, жүкке түсірілген күштер жұмыстарының қосындысы:

 Дж. Модулін қабылдаймыз. А = 183 кДж.
Дж. Модулін қабылдаймыз. А = 183 кДж.
7 -мысал. Шахта лифтісі v0 =12 м/с жылдамдықпен төмен қарай қозғалады. Лифтінің массасы 6т. Егер лифтіні ұстап тұратын арқан үзілетін болса, онда лифтіні s=10 м жолда тоқтату үшін, сақтан-дырушы парашют лифті мен шахтаның арасында қандай шамада үйкеліс күшін пайда болдыруы қажет? Үйкеліс күшін тұрақты деп санаймыз.
 Шешуі. Материялық нүктеге түсірілген
Шешуі. Материялық нүктеге түсірілген 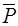 салмақ күшін және
салмақ күшін және  күшін көрсетеміз (15.13-сурет). Материялық нүктенің кинети-калық энергиясының өзгеруі туралы теореманы пайдаланамыз:
күшін көрсетеміз (15.13-сурет). Материялық нүктенің кинети-калық энергиясының өзгеруі туралы теореманы пайдаланамыз:
 .
.
Материялық нүктеге түсірілген күштердің  орын ауыстыруында жұмысын есептейміз:
орын ауыстыруында жұмысын есептейміз:
 .
.
Материялық нүкте төмен қарай қозғалатын болғандықтан салмақ күшінің жұмысы оң шама болады:
 .
.
Үйкеліс күшінің жұмысы теріс шамаға тең, себебі үйкеліс күші мен орын ауыстыру бағыттары қарама-қарсы: 
Соңғы уақыт мезгілінде лифтінің тоқтайтынын есепке ала отырып  , кинетикалық энергияның өзгеруі туралы теоремаға қоямыз:
, кинетикалық энергияның өзгеруі туралы теоремаға қоямыз:

Осыдан: 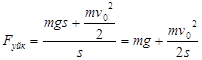 ;
;
 кН.
кН.

15.10.5. Ауырлық күштің серіппе күштің және тартылу күшінің жұмыстары.
1-есеп. Ауырлық күшінің жұмысы. Ауырлық күші әсеріндегі  нүкте
нүкте  жағдайға өткен болсын (15.14-сурет). Ауырлық күшінің жұмысы неге тең?
жағдайға өткен болсын (15.14-сурет). Ауырлық күшінің жұмысы неге тең?
Шешуі. Ауырлық күші  ның координат өстеріндегі проекцияларды төмендегідей болады:
ның координат өстеріндегі проекцияларды төмендегідей болады:

ауырлық күшінің элементар жұмысы: 
 Ал, нукте
Ал, нукте  ден
ден 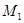 жағдайға келгенде
жағдайға келгенде  күштің жұмысы:
күштің жұмысы:

 деп белгілесек.
деп белгілесек.
 (15.76)
(15.76)
Егер механикалық жүйе қозғалысы қарастырылып жатқан болса, жүйе ауырлық күшінің жұмысы осы жүйе ауырлық күшімен инерция центрі вертикаль көшуінің көбейтіндісіне тең, яғни: 
Бұл жерде  инерция (масса) центрінің вертикаль көшуін өрнектейді.
инерция (масса) центрінің вертикаль көшуін өрнектейді.
2-есеп. Серпімділік күшінің жұмысы. А ұшы бекітілген серіппенің деформацияланбаған жағдайдайдағы ұзындығы 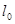 болсын. Санақ басы деп серіппенің деформацияланбаған В ұшын аламыз (15.15-сурет). Серпімділік күшінің жұмысы неге тең?
болсын. Санақ басы деп серіппенің деформацияланбаған В ұшын аламыз (15.15-сурет). Серпімділік күшінің жұмысы неге тең?
Шешуі. Серіппені шамалы созсақ, серіппенің серпімділік күші 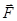 келіп шығады. Бұл күш серіппенің һ созылуына пропорционал:
келіп шығады. Бұл күш серіппенің һ созылуына пропорционал:  . Мұндағы х-серіппе деформациясы.
. Мұндағы х-серіппе деформациясы.
Серпімділік күшінің жұмысы (15.74) формулаға сәйкес төмендегідей анықталады:
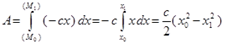 (15.77)
(15.77)
15.10.4. Қуат. Уақыт бірлігіне қатысты алынған жұмыс қуат деп аталады. Қуатты N деп алсақ, онда оны мына формуламен анықтаймыз:
 . (15.78)
. (15.78)
Мұндағы  элементар жұмысты (3.45) формуласымен алатын болсақ, онда қуат күш пен жылдамдықтың скалярлық көбейтіндісіне тең:
элементар жұмысты (3.45) формуласымен алатын болсақ, онда қуат күш пен жылдамдықтың скалярлық көбейтіндісіне тең:
 . (15.79)
. (15.79)
Қуат бірлігі үшін (БХЖ) жүйесінде 1-ватт (1Вт =1Дж/сек) алы-нады. Практикада қуаттың ірі бірлік өлшемі киловатт (1квт = 103 Вт) жиі қолданылады.
15.10. Жылжымайтын осьті айналатын қатты денеге әсер ететін күштің жұмысы мен қуаты.
3-есеп. Айналып тұрған денеге қойылған күштің жұмысы неге тең?
 Шешуі. Oz қозғалмайтын өсь төңірегінде айналатын дененің М нүктесіне
Шешуі. Oz қозғалмайтын өсь төңірегінде айналатын дененің М нүктесіне 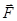 күші әсер ететін болсын (16.24-сурет). М нүктеден Oz -ке дейінгі қашықтықты h-пен белгілейміз. (15.74) формулаға сәйкес
күші әсер ететін болсын (16.24-сурет). М нүктеден Oz -ке дейінгі қашықтықты h-пен белгілейміз. (15.74) формулаға сәйкес 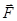 күштің
күштің  элементар доғаны өткендегі орындаған жұмысы
элементар доғаны өткендегі орындаған жұмысы 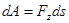 , немесе
, немесе 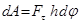 болады. Бірақ,
болады. Бірақ, 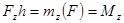
Сондықтан,  (15.80)
(15.80)
Демек, қозғалмайтын өсь төңірегінде айналып тұрған денеге қойылған күштің элементар жұмысы күштің айналу өсіне қатысты моменті мен элементар бұрылу бұрышының көбейтіндісіне тең (15.15-сурет). Дене шектелген  , бұрышқа айналғандағы күштің жұмысы
, бұрышқа айналғандағы күштің жұмысы
 (15.81)
(15.81)
Егер  болса (15.81) төмендегідей жазылады.
болса (15.81) төмендегідей жазылады.
 (15.82)
(15.82)
Осы денеге қойылған күштің қуатын анықтайық:
 (15.83)
(15.83)
Демек, айналып тұрған денеге қойылған күштің қуаты оның айналу өсіне қатысты моменті мен дененің бұрыштық жылдамдығының көбейтіндісіне тең.
15.10. Материялық нүктенің және механикалық жүйенің кинетикалық энергиясының өзгеруі туралы теорема
1. Материялық нүктенің кинетикалық энергиясының өзгеруі туралы теорема
Енді кинетикалық энергияның өзгерісінің күшпен байланысын беретін теоремаға тоқталайық. Ол теореманы негізгі теңдеуден қорытып шығарамыз. Сол мақсатпен негізгі теңдеуді алайық та оның екі жағын да d  элементар орын ауыстыруға көбейтейік:
элементар орын ауыстыруға көбейтейік:
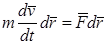 .
.
Бұл теңдеудің сол жағын түрлендірейік:  .
.
Осы түрлендіру нәтижесін пайдаланып алдыңғы теңдеуді мына түрде қайта жазайық:
 , (15.84)
, (15.84)
мұндағы штрих элементарлық жұмыстың жалпы жағдайда қандай да бір фунқцияның толық дифференциалы емес екендігін көрсетеді.
Кинетикалық энергия мен элементар жұмыс белгілеулерін пайдаланып (15.84) теңдігін қайта жазайық:
dT = d'A. (15.85)
(15.84) не болмаса (15.85) теңдігі дифференциалдық түрдегі теореманың өрнегін береді.
Теорема 10. Материялық нүктенің кинетикалық энергиясының дифференциалы оған әсер ететін күштің элементар жұмысына тең.
Енді материялық нүкте өзінің траекториясы, АВ қисығы бойымен М0М1 жолын жүріп өтсін. Бұл жолда материялық нүкте жылдамдығы  0-ден
0-ден  1-ге дейін өзгереді. (15.58) теңдігінің екі жағынан да
1-ге дейін өзгереді. (15.58) теңдігінің екі жағынан да  доғасы бойымен қисық сызықты интеграл алайық:
доғасы бойымен қисық сызықты интеграл алайық:
 .
.
Бұл теңдіктің сол жағындағы қисық сызықты интеграл кинетикалық энергияның соңғы және бастапқы мәндерінің айырмасына тең:
 . (15.86)
. (15.86)
Егер материялық нүктенің бастапқы орындағы кинетикалық энергиясын T0 деп, ал соңғы орындағысын T1 деп белгілесек және күш жұмысының (15.75) – теңдіктегі анықтамасын ескерсек, (15.75) теңдігін қысқа түрде былай жазамыз:
 . (15.87)
. (15.87)
Теорема 11. Нүктенің қандай да бір орын ауыстыруындағы кинетикалық энергиясының өзгеруі сол орын ауыстырудағы оған әсер етуші күштің жұмысына тең.
Кинетикалық энергияның өзгеруі туралы теоремадан қай жағдайда бірінші интеграл алуға болатынын анықтау үшін алдымен күш жұмысының негізгі қасиеттерін зерттеп білуіміз керек.
2. Механикалық жүйенің кинетикалық энергиясының өзгеруі туралы теорема
Бізге n материялық нүктелердің механикалық жүйесі берілсін жүйенің  нүктесіне әсер етуші барлық сыртқы күштердің теңәсерлі күшін
нүктесіне әсер етуші барлық сыртқы күштердің теңәсерлі күшін  деп, ал ондағы ішкі күштердің теңәсерлі күшін
деп, ал ондағы ішкі күштердің теңәсерлі күшін 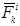 деп белгілейміз. Сонда массасы
деп белгілейміз. Сонда массасы  -ға тең, бұл
-ға тең, бұл  нүктесінің қозғалысының дифференциалдық теңдеуін мынадай түрде жаза аламыз:
нүктесінің қозғалысының дифференциалдық теңдеуін мынадай түрде жаза аламыз:
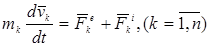 . (15.88)
. (15.88)
Бұл теңдеудің әрқайсысын  шамасына көбейтіп, өзара қоссақ, сонда:
шамасына көбейтіп, өзара қоссақ, сонда:
 . (15.89)
. (15.89)
Бұл соңғы теңдеудің сол жағындағы қосынды:
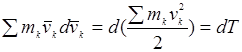 .
.
Болғандықтан (15.89) теңдігін мына түрде аламыз:
 . (15.90)
. (15.90)
Егер  күштерінің элементар жұмыстарына сәйкес
күштерінің элементар жұмыстарына сәйкес

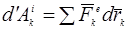 , (15.91)
, (15.91)
деп белгілесек, онда (15.90) теңдігін қайтадан мына түрде жазған болар едік:
 . (15.92)
. (15.92)
(15.90) немесе (15.92) формуласы механикалық жүйенің кинети-калық энергиясының өзгеруі туралы теореманың дифференциалдық түрдегі математикалық өрнегін көрсетеді.
Теорема 12. Механикалық жүйенің кинетикалық энергиясының дифференциалы жүйеге әсер етуші барлық сыртқы және ішкі күштердің элементарлық жұмыс-тарының қосындысына тең болады.
Жүйенің алғашқы орналасу жағдайына сәйкес кинетикалық энергиясын  деп, ал оның ақырғы жағдайындағы кинетикалық энергиясын
деп, ал оның ақырғы жағдайындағы кинетикалық энергиясын  деп белгілейік. (15.92) теңдігінің екі жағынан да жүйенің осы екі орналасу аралығында сәйкес шектерде интеграл алайық:
деп белгілейік. (15.92) теңдігінің екі жағынан да жүйенің осы екі орналасу аралығында сәйкес шектерде интеграл алайық:
 . (15.93)
. (15.93)
немесе,
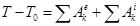 . (15.94)
. (15.94)
Бұл теңдіктегі 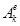 және
және 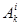 жүйенің
жүйенің  нүктесіндегі
нүктесіндегі  және
және  - күштердің сол нүктенің траектория бойымен жүрген
- күштердің сол нүктенің траектория бойымен жүрген  жолындағы жұмысы:
жолындағы жұмысы:

 . (15.95)
. (15.95)
Сөйтіп, жүйенің кинетикалық энергиясының өзгеруі туралы теореманың интегралдық түрдегі өрнегі (15.93) немесе (15.94) теңдігімен беріледі. Теорема бұл түрінде былай айтылады:
Теорема 13. механикалық жүйенің бір орналасу жағдайынан екінші бір орналасу жағдайына көшу кезінде жасаған орын ауыстыруындағы кинети-калық энергиясының өзгеруі жүйеге әсер етуші барлық сыртқы және ішкі күштердің сол орын ауыстыруындағы жұмыстарының қосындысына тең болады.
 8-мысал. Салмағы
8-мысал. Салмағы  пойыз өрге қарай түзу сызықты, ілгерілемелі қозғалады;
пойыз өрге қарай түзу сызықты, ілгерілемелі қозғалады; 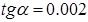 . Оның қозғалысына кедергі күші пойыздың салмағының
. Оның қозғалысына кедергі күші пойыздың салмағының  -ның
-ның  -ын құрайды. 750м жол жүргенде жылдамдығы 18-ден 36 км/сағ-қа өзгереді (15.16-сурет).
-ын құрайды. 750м жол жүргенде жылдамдығы 18-ден 36 км/сағ-қа өзгереді (15.16-сурет).
Локомотивтің тұрақты тарту күшін анықтау керек.
Шешуі. Пойыздың ілгерілемелі қозғалысын материялық нүктенің қозғалысы ретінде қарастырып, 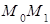 орын ауыстыруында нүктенің кинетикалық энергиясының өзгеруі туралы теореманы пайдаланамыз. Осы орын ауыстыруда пойыздың жылдамдығы
орын ауыстыруында нүктенің кинетикалық энергиясының өзгеруі туралы теореманы пайдаланамыз. Осы орын ауыстыруда пойыздың жылдамдығы 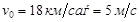 -тан
-тан 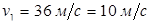 -қа өседі.
-қа өседі.
Пойызға әсер ететін күштер: локомотивтің тарту күші  , пойыздың салмақ күші
, пойыздың салмақ күші  , рельстің нормаль реакция күші
, рельстің нормаль реакция күші  және қозғалысына кедергі күші
және қозғалысына кедергі күші 
 , ал
, ал 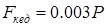 .
.
 тарту күшінің
тарту күшінің  орын ауыстырғандағы жұмысы мынаған тең:
орын ауыстырғандағы жұмысы мынаған тең:
 .
.
Пойыздың  салмақ күшінің жұмысы, вертикаль
салмақ күшінің жұмысы, вертикаль  орын ауыстыруына байланысты және мынаған тең:
орын ауыстыруына байланысты және мынаған тең:  ,
,
мұндағы  -бұрышы өте аз болғандықтан
-бұрышы өте аз болғандықтан  және:
және:
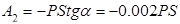 .
.
 жылдамдығына перпендикуляр, рельстің реакция
жылдамдығына перпендикуляр, рельстің реакция  күшінің жұмысы нөлге тең.
күшінің жұмысы нөлге тең.
Кедергі  күшінің
күшінің  орын ауыстырғандағы жұмысы мынаған тең:
орын ауыстырғандағы жұмысы мынаған тең:
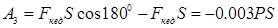 .
.
Пойыздың  массасының шамасын және барлық күштер жұмыстарының шамаларын (3.132)-теңдеуге қойып алатынымыз:
массасының шамасын және барлық күштер жұмыстарының шамаларын (3.132)-теңдеуге қойып алатынымыз:
 .
.
Локомотивтің тарту күшінің шамасын табамыз:
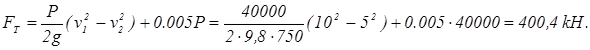
№16. ДӘРІС ДИНАМИКАНЫҢ ЖАЛПЫ ТЕОРЕМАЛАРЫН ҚАТТЫ ДЕНЕ ДИНАМИКАСЫНА ҚОЛДАНУ.
1. Қозғалмайтын өс төңірегінде айналатын қатты дененің қозғалыс мөлшерінің моменті. Қатты дене қозғалмайтын OZ өсін  бұрыштық жылдамдықпен айнала қозғалатын болсын (16.1-сурет). Осы дененің О центріне қатысты кинетикалық моментін анықтайық. Анықтама бойынша:
бұрыштық жылдамдықпен айнала қозғалатын болсын (16.1-сурет). Осы дененің О центріне қатысты кинетикалық моментін анықтайық. Анықтама бойынша:
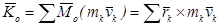 . (16.1)
. (16.1)
 Координаттық өстердегі
Координаттық өстердегі 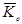 векторының проекциялары (15.36) формулаларымен анықталады. Жылдамдық
векторының проекциялары (15.36) формулаларымен анықталады. Жылдамдық  векторының проекцияларын анықтауға Эйлер формуласын қолдануға болады:
векторының проекцияларын анықтауға Эйлер формуласын қолдануға болады:
 . (16.2)
. (16.2)
Осы теңдіктен: 

 . (16.3)
. (16.3)
жылдамдықтар проекцияларының өрнектерін (15.36) формуладағы орындарына қоямыз:
 . (16.4)
. (16.4)
Осы (3.103) формуладағы қосындыларды мына төмендегідей етіп белгілейміз:


 . (16.5)
. (16.5)
Осыларға ұқсас формулалармен анықталатын, бірақ (3.104) өрнегінде жоқ тағы бір үш шаманы көрсетейік:


 . (16.6)
. (16.6)
(16.5), (16.6) теңдіктерімен анықталатын шамалар инерция моменттері деп аталады. Олардың ішіндегі  үш шаманы дененің центрден тепкіш инерция моменттері деп, ал қалғандары
үш шаманы дененің центрден тепкіш инерция моменттері деп, ал қалғандары  дененің өстік инерция моменттері деп аталады.
дененің өстік инерция моменттері деп аталады.
Енді осы анықтамаларды пайдалансақ (16.4) формулаларын мына түрге келтіреміз: 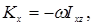

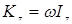 . (16.7)
. (16.7)
2. Қатты дененің жылжымайтын осьті айналып қозғалуының дифференциалдық теңдеуі
Дененің қозғалмайтын өс төңірегіндегі айналмалы қозғалысының дифференциалдық теңдеуін алу үшін қозғалыс мөлшер моментінің өзгеруі туралы теореманы (15.51) теңдеулерінің үшінші түріне сәйкес қолдануымыз керек:
 . (16.8)
. (16.8)
Дененің Z айналу өсіне қатысты алынған қозғалыс мөлшер моменті (16.7) формулаларының 3 – сі бойынша анықталады:
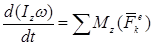 . (16.9)
. (16.9)
Дене абсолют қатты дене болған жағдайда  инерция моменті тұрақты шама болады. Олай болса (16.9) теңдеуін былайша өзгерте аламыз:
инерция моменті тұрақты шама болады. Олай болса (16.9) теңдеуін былайша өзгерте аламыз:
 , (16.10)
, (16.10)
немесе  . (16.11)
. (16.11)
 Осы соңғы теңдеу қатты дененің қозғалмайтын өс төңірегіндегі айналмалы қозғалысының дифференциалдық теңдеуі болып табы-лады.
Осы соңғы теңдеу қатты дененің қозғалмайтын өс төңірегіндегі айналмалы қозғалысының дифференциалдық теңдеуі болып табы-лады.
1-мысал. Горизонталь  өсті айнала қозғалатын радиусы
өсті айнала қозғалатын радиусы  , салмағы
, салмағы  -ге тең шкивке трос оралған. Тростың соңына салмағы
-ге тең шкивке трос оралған. Тростың соңына салмағы  -ға тең жүк ілінген. Шкивке тұрақты айналдырушы момент түсірілген (16.2-сурет).
-ға тең жүк ілінген. Шкивке тұрақты айналдырушы момент түсірілген (16.2-сурет).
Көтерілетін жүктің  үдеуін табу керек.
үдеуін табу керек.
Шешуі. Жүктің  жылдамдығына тең шкивтің бетіндегі кез келген нүктесінің жылдамдығын
жылдамдығына тең шкивтің бетіндегі кез келген нүктесінің жылдамдығын 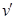 деп белгілеп, жүк және шкивтен құрылған механикалық жүйенің
деп белгілеп, жүк және шкивтен құрылған механикалық жүйенің  өсіне қатысты кинетикалық моментін анықтаймыз:
өсіне қатысты кинетикалық моментін анықтаймыз:
 ,
,
мұндағы:  шкивтің
шкивтің  өсіне қатысты инерция моменті;
өсіне қатысты инерция моменті; 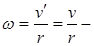 шкивтің бұрыштық жылдамдығы;
шкивтің бұрыштық жылдамдығы; 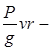 жүктің
жүктің  өсіне қатысты қозғалыс мөлшер моменті.
өсіне қатысты қозғалыс мөлшер моменті.
Мәндерін орындарына қоямыз:  .
.
Жүйеге түсірілген сыртқы күштердің  өсіне қатысты негізгі моменті мына түрде анықталады:
өсіне қатысты негізгі моменті мына түрде анықталады: 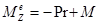 .
.
Механикалық жүйенің өске қатысты кинетикалық моментінің өзгеруі туралы теореманы пайдаланамыз:
 ,
, 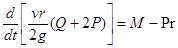 ,
,  ,
,
мұндағы, 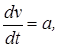 сондықтан:
сондықтан: 
 2-мысал. Салмағы Р, радиусы
2-мысал. Салмағы Р, радиусы 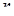 шкивті айналмалы қозғалысқа келтіретін белдіктің тартылыс күштері Т1 және Т2 (16.3-сурет).
шкивті айналмалы қозғалысқа келтіретін белдіктің тартылыс күштері Т1 және Т2 (16.3-сурет).
Бұрыштық жылдамдығы 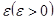 тұрақты болатын шкивке түсірілген Мкед кедергі моментін анықтау керек. Шкив біртекті дөңгелек диск.
тұрақты болатын шкивке түсірілген Мкед кедергі моментін анықтау керек. Шкив біртекті дөңгелек диск.
Шешуі. Шкивтің OZ өсін айнала қозғалысының
дифференциалдық теңдеуін құрамыз:  ,
,
мұндағы,  – шкивтің айналу өсіне қатысты инерция моменті.
– шкивтің айналу өсіне қатысты инерция моменті.
Осыдан, белгісіз кедергі моментін анықтаймыз:  .
.
№ 17. Материялық нүкте және механикалық жүйе үшін Даламбер принципі. Заттық нүкте мен механикалық жүйеге Даламбер қағидасын қолдану.
17.1 Материялық нукте үшін Даламбер принципі.
Динамиканың мәселелерін шешкен кезде барлық әдістер Ньютон заңдарынан келіп шығатын теңдеулерге немесе динамиканың жалпы теоремаларына негізделеді.
Техникада кездесетін көптеген мәселелерді шешкен кезде механиканың жалпы принциптерінен пайдалану өте қолайлы. Бұл принциптердің бірі Даламбер принципі. Даламбер принципінде динамика теңдеулеріне статика теңдеулерінің түрі беріледі.
Еркін материялық нүкте үшін Даламбер принципін келтіріп шығару үшін
динамиканың негізгі теңдеуінен пайдаланамыз:
 ,
,
немесе
 . (17.1)
. (17.1)
Шамасы материялық нүктенің массасы мен оның үдеуінің көбейтіндісіне тең болып, бағыты үдеу векторының бағытына қарама-қарсы бағытталған вектор инерция күші деп аталады, яғни
 (17.2)
(17.2)
(17.2) ні (17.1) ге қойсақ
 (17.3)
(17.3)
келіп шығады.
 (17.3) өрнегі еркін қозғалатын материялық нүкте үшін Даламбер принципін анықтайды: Материялық нүктеге әсер ететін актив күш инерция күшімен бірге тепе-теңдікте тұрған күштер жүйесін құрайды (17.1- сурет).
(17.3) өрнегі еркін қозғалатын материялық нүкте үшін Даламбер принципін анықтайды: Материялық нүктеге әсер ететін актив күш инерция күшімен бірге тепе-теңдікте тұрған күштер жүйесін құрайды (17.1- сурет).
Егер материялық нүкте қисық сызық бойлап қозғалатын болса, онда инерция күші жанама және нормал құраушыларға ажратылады:
 .
.
17.1-сурет
Мұнда
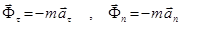 ,
,
немесе
 ,
, 
Егер материялық нүкте түзу сызық бойлап қозғалатын болса, онда 
Еркін емес материялық нүкте үшін Даламбер принципі төмендегідей жазылады:
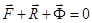 (17.4)
(17.4)
Бұл өрнектегі  байланыс реакция күшін білдіреді.
байланыс реакция күшін білдіреді.
17.2 Система үшін Даламбер принципі
Механикалық жүйе бір-бірімен байланыста болған  материялық нүктелер құрамынан тұрсын. Бұл системаға әсер ететін күштерді сыртқы және ішкі күштерге ажыратсақ, онда жүйенің әр-бір нүктесі үшін Даламбер принципін төмендегідей көріністе жазамыз:
материялық нүктелер құрамынан тұрсын. Бұл системаға әсер ететін күштерді сыртқы және ішкі күштерге ажыратсақ, онда жүйенің әр-бір нүктесі үшін Даламбер принципін төмендегідей көріністе жазамыз:
 (17.5)
(17.5)
Демек, механикалық жүйенің әр-бір нүктесіне әсер ететін сыртқы және ішкі күштер инерция күшімен бірге алынғанда олар әр кезде тепе-теңдікті құрайды. (17.5) арқылы өрнектелген теңдеулерді бірме-бір қоссақ, онда
 (17.6)
(17.6)
келіп шығады. (17.6) өрнектегі  сыртқы күштердің бас векторы,
сыртқы күштердің бас векторы,  ішкі күштердің бас векторы,
ішкі күштердің бас векторы,  инерция күштерінің бас векторы.
инерция күштерінің бас векторы.
Ішкі күштердің қасиетіне сәйкес 
Нәтижеде (17.6) өрнегін төмендегідей көріністе жазуға болады, яғни
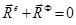 . (17.7)
. (17.7)
Сонымен: Системаға әсер етуші сыртқы күштердің бас векторы мен инерция күштерінің бас векторының геометриялық қосындысы нольге тең.
Егер (17.6) - өрнекті нүктелердің  радиус-векторларына векторлік көбейтіп бұдан пайда болған натижелерді бір-біріне қоссақ, онда
радиус-векторларына векторлік көбейтіп бұдан пайда болған натижелерді бір-біріне қоссақ, онда
 (17.8)
(17.8)
келіп шығады. Бұл жердегі  О нүктеге қатысты сыртқы күштердің моменті;
О нүктеге қатысты сыртқы күштердің моменті;  инерция күштерінің бас моменті;
инерция күштерінің бас моменті; 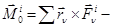 ішкі күштердің бас моменті; бірақ ішкі күштердің қасиеттерінен
ішкі күштердің бас моменті; бірақ ішкі күштердің қасиеттерінен  . Бұл жағдайда (17.8) - өрнекті төмендегідей көріністе жазуға болады:
. Бұл жағдайда (17.8) - өрнекті төмендегідей көріністе жазуға болады:
 . (17.9)
. (17.9)
Яғни, системага әсер етуші сыртқы күштер мен оның нүктелерінің инерция күштерінен бірер-бір орталыққа қатысты алынған моменттерінің қосындысы нөлге тең. Біргелікте алынған (17.7) және (17.9) теңдеулері механикалық жүйе үшін Даламбер принципінің векторлік көрінісін береді.
Бұл өрнектерді Декарт координата өстеріне проекцияласақ, онда механикалық жүйе үшін Даламбер принципінің аналитикалық шартын өрнектейтін теңдеулерді табамыз:
 (17.10)
(17.10)
Егер біз системаның масса орталығының қозғалысы және кинетикалық моментінің өзгеруі жөніндегі теоремаларды
 (17.11)
(17.11)
 (17.12)
(17.12)
(17.7),(17.9) өрнектермен салыстырсақ, онда инерция күштерінің бас векторы және бірер-бір орталыққа қатысты олардың бас моментін анықтайтын формулаларды анықтаймыз, яғни
 (17.13)
(17.13)
 (17.14)
(17.14)
(17.13) мен (17.14) өрнектерден инерция күштерінің бас векторі дененің массасы мен инерция орталығының үдеу-векторінің көбейтіндісіне тең болып, бағыты үдеу-вектордің бағытына қарама-қарсы екені көрінеді. Инерция күштерінің бірер-бір орталыққа қатысты бас моменті системанинг осы орталыққа қатысты кинетикалық моментінен уақыт бойынша алынған бірінші туындысына тескері таңбалы өрнекке тең. (17.13) пен анықталатын векторлық шаманың жанама және нормаль құраушылары төмендегідей формулалардан табылады
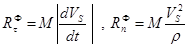 (17.15)
(17.15)
Енді кейбір жеке жағдайлар үшін (17.13), (17.14) формулаларынан пайдаланып инерция күштерінің бас векторі мен бас моментінің есептелетін формулаларын келтіріп шығарайық.
1.Дене ілгерілемелі қозғалыста болсын. Бұл жағдайда дене инерция орталығы төңірегінде айланбайды. Демек  болып, инерция күштері тең әсер етуші күшке келтіріледі және ол инерция күштерінің бас векторы сияқты анықталады .
болып, инерция күштері тең әсер етуші күшке келтіріледі және ол инерция күштерінің бас векторы сияқты анықталады .
2.Қозғалыстағы дене симметрия жазықтығына ие болып, ол осы жазықтыққа тік бағытталған қозғалмайтын өсь төңірегінде айналып тұрған болсын. Онда инерция күштерінің бас векторы (17.13), ал инерция күштерінің бас моменті (17.14) теңдеулерін қозғалмайтын өске проекциялаудан анықталады:
 . (17.16)
. (17.16)
17.2- сурет 
| Егер айлану өсі дене массасының орталығынан өтсе, онда  болады.
3.Дене симметрия жазықтығына ие болып, оған параллель қозғалатын болса, онда инерция күштерінің бас векторі болады.
3.Дене симметрия жазықтығына ие болып, оған параллель қозғалатын болса, онда инерция күштерінің бас векторі  болады. Оның өстерге болған проекциялары болады. Оның өстерге болған проекциялары
 , ал бас моменті , ал бас моменті 
|
Бұл жердегі  дененің инерция орталығына қатысты инерция моменті.
дененің инерция орталығына қатысты инерция моменті.
Демек, жазық-параллель қозғалатын денеге қойылатын инерция күштері бір бас вектор мен бір бас моментке келтіріледі (17.2-сурет).
Даламбер принципін динамикаға қатысты есептерге қолданған кезде олар төмендегідей тәртіпте шешіледі.
1.Санақ жүйесі енгізіледі.
2.Денеге әсер етуші актив (сыртқы) және пассив (реакция) күштері суретте көрсетіледі.
3.Инерция күштерінің бас векторы мен бас моменті анықталады. Сонымен қатар инерция күштерінің бас векторының қойылу нүктесі табылады.
4.Анықталған күштер жүйесінің «тепе-теңдік» теңдеулері түзіледі.
5.Түзілген теңдеулерден белгісіздер анықталады.
Мысал . Массасы m=60 кг болған B жүгі радиусы r=0,4 м барабанға  оралған жіпке асылған. Барабан
оралған жіпке асылған. Барабан  заң бойынша айланады. Жіптің кернеу күші анықталсын (18.3-сурет).
заң бойынша айланады. Жіптің кернеу күші анықталсын (18.3-сурет).
Шешуі. Санақ системасы үшін 18.3-суретте көрсетілгендей табиғи координата жүйесін таңдаймыз. B жүкті материалды нүкте ретінде қабылдасақ, онда оған ауырлық күші  ,
,
жіптің кернеу күші  әсер етеді. Жүктің
әсер етеді. Жүктің  үдеуі барабанның бойындағы нүктенің жанама үдеуімен шама жағынан бірдей болғандықтан жүктің инерция күші
үдеуі барабанның бойындағы нүктенің жанама үдеуімен шама жағынан бірдей болғандықтан жүктің инерция күші
18.3-сурет
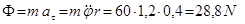 болады.
болады.
Жүктің инерция күшін  ті нүктеге әсер етуші күштер қатарына қосып қарасақ, онда нүкте үшін Даламбер принципін төмендегідей түрде жазамыз
ті нүктеге әсер етуші күштер қатарына қосып қарасақ, онда нүкте үшін Даламбер принципін төмендегідей түрде жазамыз
 ,
,
Немесе
 .
.
Бұл жерден

келіп шығады.
Өрнектің сан мәндерін қойсақ
T=616,8 Н.
шығады.
№18. ДӘРІС ҚОЗҒАЛУ МҮМКІНШІЛІК ПРИНЦИПІ
Байланыстар классификациясы
Бірнеше денеден құрылған жүйенің тепе-теңдігін қарастырғанда Лагранждың Қозғалу мүмкіншілік принціпінен пайдалану мақсатқа сай. Қозғалу мүмкіншілік принципін беруден алдын біз байланыс түрлерімен танысайык.
Жүйе нүктелерінің қозғалысын шектейтін (яғни жүйені еріксіз ететін) шарт байланыс деп аталады. Жүйеге қойылған байланыстардың себебінен жүйе нүктелерінің координаттары, жылдамдықтары еркін өзгере алмайды. Байланыстардың жүйеге немесе оның нүктелерінің қозғалысына тигізетін әсерін схемалық түрде геометриялық сызықтар, беттер арқылы елестете аламыз. Осыған сәйкес байланыстардың денеге көрсеткен әсерлерін математикалық теңдеулер түрінде өрнектеу мүмкін. Бұл теңдеулер байланыс теңдеулері деп аталады. Байланыс теңдеулері жүйеге қатысты нүктелердің координаталары, олардың жылдамдықтары және уақыт арқылы өрнектелуі мүмкін. Жүйе нүктелерінің тек координаталарына ғана шек қоятын байланыстар геометриялық байланыстар деп аталады және төмендегідей көріністегі теңдеулер арқылы өрнектеледі:
 ,
,  (18.1)
(18.1)
 (18.2)
(18.2)
Егер байланыс жүйе нүктелерінің тек координаталарына ғана шек қоймай олардың жылдамдықтарына да шек қоятын болса, онда мұндай байланыс кинематикалық (дифференциалды) байланыс деп аталады. Бұл байланыстың теңдеуі
 (18.3)
(18.3)

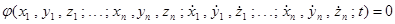 (18.4)
(18.4)
көріністерінде жазылады.
Егер (18.3) және (18.4) теңдеулер интегралланатын болса, онда ол голономды, олай болмаған жағдайда голономды емес байланыс делінеді.
Байланыс теңдеуі уақытқа тікелей
тәуелді болмаса, онда мұндай байланыс стационар байланыс, ал уақытқа тікелей байланысты болса, онда мұндай байланыс стационар емес байланыс деп аталады. Демек (18.1) және (18.3) стационар, (18.2) мен (18.4) стационар емес байланыстардың теңдеулерін береді. Мәселен, 18.1-суретте көрсетілген кривошип-шатунды механизмнің кез-келген уақытта алатын орнын оның O , A және B нүктелерінің алатын орындары арқылы анықтау үшін байланыстардың төмендегідей теңдеулерін жазамыз:
 (18.5)
(18.5)
(18.5) байланыс теңдеулері О нүктенің қозғалмайтындығын , ОА және АВ стержендердің ұзындықтарының өзгермейтіндігін, сонымен қатарВ нүктенің  өсі бойымен жылжуын сипаттайды. (18.5) арқылы анықталатын байланыс теңдеулері уақытқа тікелей байланысты емес. Сол үшін себептен де олар стационар байланыстарды өрнектейді.
өсі бойымен жылжуын сипаттайды. (18.5) арқылы анықталатын байланыс теңдеулері уақытқа тікелей байланысты емес. Сол үшін себептен де олар стационар байланыстарды өрнектейді.
 Енді кривошип-шатунды механизмнің ползуны еденнің бетінде сырғанай отырып вертикаль бағытта
Енді кривошип-шатунды механизмнің ползуны еденнің бетінде сырғанай отырып вертикаль бағытта  заңы бойынша гармоникалық тербелісте болсын. Онда
заңы бойынша гармоникалық тербелісте болсын. Онда  қарастырылып жатқан жүйенің байланыс теңдеулері төмендегідей:
қарастырылып жатқан жүйенің байланыс теңдеулері төмендегідей:
 (18.6)
(18.6)
(18.6) теңдеудің екіншісі уақытқа байланысты. Демек , бұл байланыс стационар емес байланыс.
Жүйеге қойылған байланыстар босатылатын және босатылмайтын болып бөлінеді. Егер байланыс теңдік арқылы өрнектелсе босатылмайтын, ал байланыс теңдеуі теңсіздік түрінде өрнектелетін болса, онда ол босатылатын байланыс делінеді.
2. Ортақталған координаттар. Жүйенің еркін қозғалу дәрежесі
Еріксіз механикалық жүйе нүктелерінің көшуі еркін болмастан, қандайда бір себеппен шегараланатыны белгілі. Бұл жүйе нүктелерінің барлық координаттары еркін түрде өзгермейтінін көрсетеді. Ал еріксіз координаталар байланыс теңдеулерінен табылады.
Айталық, жүйе  нүктелерден құралған болып, оған s голономды байланыс қойылған:
нүктелерден құралған болып, оған s голономды байланыс қойылған:

Демек, жүйе нүктелерінің 3n координаттары арасында s байланыс бар, яғни s координат еріксіз. Ал, жүйе нүктелерінің еркін координаттар саны k=3n-s координат арқылы анықталады.
Голономды байланыста болған жүйенің бірден-бір орнын анықтайтын өзара тәуелді болмаған параметрлер саны жүйенің еркіндік дәрежесі деп аталады.
Мысалы, 18.1-суретте көрсетілген кривошип-шатунды механизмді алатын болсақ, оның кез-келген уақытта алатын орнын  арқылы анықтауға болады. Егер механизмнің орнын x2арқылы анықтайтын болсақ, онда x3және y2 лерді (18.5) теңдеулер жүйесінен табуға болады. Механизмнің кез-келген уақытта алатын орнын анықтау үшін OAкривошиптің айналу
арқылы анықтауға болады. Егер механизмнің орнын x2арқылы анықтайтын болсақ, онда x3және y2 лерді (18.5) теңдеулер жүйесінен табуға болады. Механизмнің кез-келген уақытта алатын орнын анықтау үшін OAкривошиптің айналу  бұрышын алуға да болады. Демек, бұл механизмнің еркіндік дәрежесі бірге тең.
бұрышын алуға да болады. Демек, бұл механизмнің еркіндік дәрежесі бірге тең.
Жүйенің кеңістіктегі алатын орнын бірден-бір анықтайтын өзара тәуелді болмаған параметрлер Ортақталған координаталар делінеді және оларды  деп белгілейді. Ортақталған координаталардың өлшем бірлігі әртүрлі болуы мүмкін ( мәселен, метр, радиан, м2 , м3 ). 18.1-суретте көрсетілген кривошип-шатунды механизмнің кез-келген уақытта алатын орнын бір ғана координата
деп белгілейді. Ортақталған координаталардың өлшем бірлігі әртүрлі болуы мүмкін ( мәселен, метр, радиан, м2 , м3 ). 18.1-суретте көрсетілген кривошип-шатунды механизмнің кез-келген уақытта алатын орнын бір ғана координата  арқылы анықтауға болады.
арқылы анықтауға болады.
Демек, голономды байланыстағы жүйенің еркіндік дәрежесі оның Ортақталған координаталар санына тең. Біз бұл бөлімде тек голономды байланыстағы жүйе ны қарастырамыз.
Егер жүйе ға  голономды болмаған байланыс қойылған болса, оның Ортақталған координаталар арасында белгілі бір қатынас болады. Мұндай жүйенің еркіндік дәрежесі
голономды болмаған байланыс қойылған болса, оның Ортақталған координаталар арасында белгілі бір қатынас болады. Мұндай жүйенің еркіндік дәрежесі  ге тең.
ге тең.
Голономды стационар байланыста болған механикалық жүйе n нүктеден тұрады деп есептейік және оның еркіндік дәрежесі k ға тең болсын. Бұл голономды жүйенің Ортақталған координаталарын  десек, онда қарастырылып жатқан жүйе нүктелерінің радиус-векторларын немесе Декарт өстеріндегі координаталарын Ортақталған координаталар арқылы төмендегідей өрнектермен өрнектеуге болады, яғни:
десек, онда қарастырылып жатқан жүйе нүктелерінің радиус-векторларын немесе Декарт өстеріндегі координаталарын Ортақталған координаталар арқылы төмендегідей өрнектермен өрнектеуге болады, яғни:
 (18.7)
(18.7)
 (18.8)
(18.8)
Олай болса, голономды байланыста тұрған механикалық
жүйенің қозғалыс теңдеулерін Ортақталған координаталар арқылы төмендегідей түрде жазуға болады:
 (18.9)
(18.9)
Ортақталған координаталардан уақыт бойынша алынған бірінші туынды Ортақталған жылдамдық, екінші туынды Ортақталған үдеу
деп аталады және олар былай жазылады:  (18.10)
(18.10)
Ортақталған жылдамдықтың өлшем бірлігі Ортақталған координатаның өлшем бірлігі мен уақыт бірлігінің қатынасына тең.
3 Мүмкін болған көшу. Мүмкін болған көшудегі жұмыс. Идеал байланыстар
 Жүйе ға қойылған байланыстардың шарттарын қанағаттандырушы кез-келген шексіз орын ауыстырулар жиыны мүмкін болған көшулер делінеді және олар
Жүйе ға қойылған байланыстардың шарттарын қанағаттандырушы кез-келген шексіз орын ауыстырулар жиыны мүмкін болған көшулер делінеді және олар  көріністе
көріністе
өрнектеледі.
Мәселен, OAB кривошип-шатунды механизмдегі Bползунының мүмкін бўлган көшуі оның горизонтал бойлап  шексіз кіші шамаға орын ауыстыруы (18.3-сурет). OA кривошиптің A нүктесінің мүмкін бўлган көшуі OA ға тік болған
шексіз кіші шамаға орын ауыстыруы (18.3-сурет). OA кривошиптің A нүктесінің мүмкін бўлган көшуі OA ға тік болған 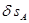 шексіз кіші шамаға орын ауыстыруы. 18.3-сурет
шексіз кіші шамаға орын ауыстыруы. 18.3-сурет
OA кривошиптің мүмкін болған көшуі, оның O нүктесінің төңірегінде шексіз кіші 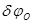 бұрышқа бұрылуынан тұрады. AB шатунның мүмкін болған көшуі P лездік орталық төңірегінде шексіз кіші
бұрышқа бұрылуынан тұрады. AB шатунның мүмкін болған көшуі P лездік орталық төңірегінде шексіз кіші  бұрышқа бұрылуы.
бұрышқа бұрылуы.
Стационар байланыстағы жүйенің негізгі көшуі осы мүмкін болған көшулердің бірімен сәйкес келеді. Еге жүйеге стационар болмаған байланыс қойылған болса, онда жүйе нүктесінің негізгі көшуі мүмкін болған көшулердің бірімен де дәлме-дәл түспеуі мүмкін. Мәселен,  өсь төңірегінде айланып тұрған дисктің радиусы бойлап қозғалатын K нүктенің негізгі көшуін тексерейік (18.4-сурет). K нүктенің негізгі көшуі төмендегідей болады:
өсь төңірегінде айланып тұрған дисктің радиусы бойлап қозғалатын K нүктенің негізгі көшуін тексерейік (18.4-сурет). K нүктенің негізгі көшуі төмендегідей болады:
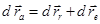
 Мұндағы K нүктенің салыстырмалы қозғалысындағы негізгі көшуін оның мүмкін болған
Мұндағы K нүктенің салыстырмалы қозғалысындағы негізгі көшуін оның мүмкін болған  көшуі арқылы өрнектеуге болады. Бұл жағдайда негізгі көшу мүмкін болған көшумен дәлме-дәл түседі.
көшуі арқылы өрнектеуге болады. Бұл жағдайда негізгі көшу мүмкін болған көшумен дәлме-дәл түседі.
18.4-сурет
Жүйенің бірер-бір нүктесіне қойылған күштің осы нүктенің Қозғалу мүмкіншілік кезіндегі атқарған жұмысы күш векторы мен Қозғалу мүмкіншілік векторының скаляр көбейтіндісіне тең, яғни

Егер жүйеге бір емес бірнеше күштер әсер етсе, онда олардың атқарған мүмкін болған жұмыстары төмендегідей формула арқылы анықталады:
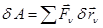 , (18.11)
, (18.11)
немесе
 . (18.12)
. (18.12)
Жүйе ға қойылған байланыстардың реакция күштерінің жүйенің мүмкін болған орын ауыстыруының кезіндегі атқарған жұмыстарының қосындысы нөлге тең болса, онда мұндай байланыстар идеал байланыстар деп аталады. Жүйе нүктелеріне қойылған байланыстардың реакция күштерін 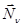 деп белгілесек, онда идеал байланыстың шартын былай жазуға болады:
деп белгілесек, онда идеал байланыстың шартын былай жазуға болады:
 (18.13)
(18.13)
4. Ортақталған координат пен ортақталған күштер
Сонымен, жүйе га қойылған күштердің Қозғалу мүмкіншілік кезіндегі атқарған жұмыстарының қосындысы (18.11) формуласымен анықталады екен. Егер (18.11) өрнекте (18.7) ні назарға алсақ, жүйе  нүктесінің мүмкін болған
нүктесінің мүмкін болған 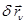 көшуі Ортақталған координаталар арқылы төмендегідей жазылады:
көшуі Ортақталған координаталар арқылы төмендегідей жазылады:
 (18.14)
(18.14)
(18.14) ті (18.11) ге апарып қойсақ:
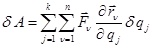 . (18.15)
. (18.15)
Төмендегідей белгілеу енгізейік:
 . (18.16)
. (18.16)
(18.16) - белгілеуге байланысты (18.15) өрнек
 (18.17)
(18.17)
көрініске ие болады.
(18.16) тенгликпен анықталушы  өрнегі
өрнегі  Ортақталған координатаға сәйкес келетін Ортақталған күш деп аталады.
Ортақталған координатаға сәйкес келетін Ортақталған күш деп аталады.
Ортақталған күшті есептеген кезде мынандай әдісті де қолдануға болады. Ортақталған  күшті есептеу үшін мүмкін болған көшудің тек
күшті есептеу үшін мүмкін болған көшудің тек  ге сәйкес келетін Ортақталған координатасы
ге сәйкес келетін Ортақталған координатасы  ғана өзгереді деп қабылданады, қалған Ортақталған координаталар бойынша Қозғалу мүмкіншілік нөлге тең деп қаралады және орын ауыстыру кезінде мүмкін болған жұмыс есептелінеді:
ғана өзгереді деп қабылданады, қалған Ортақталған координаталар бойынша Қозғалу мүмкіншілік нөлге тең деп қаралады және орын ауыстыру кезінде мүмкін болған жұмыс есептелінеді:
 .
.
Ол жағдайда
 . (18.18)
. (18.18)
Сондай-ақ Ортақталған күшті аналитикалық тәсілмен төмендегідей есептеу мүмкін:
 (18.18)
(18.18)
(18.18) ден көретініміз, Ортақталған күштің өлшемі жұмыс өлшем бірлігінің Ортақталған координат өлшем бірлігінің бөлінгеніне тең. Егер Ортақталған координат ұзындық бірлігінде өлшенсе, жалпылаған күш Ньютонда өрнектеледі, Ортақталған координата үшін бұрыш алынса, Ортақталған күш бірлігі күш моментінің бірлігі Нм- ден тұрады.
Жүйеге әсер ететін күштер потенциалдық болғанда Ортақталған күш қалай есептелінетін көрейік.
Жүйеге әсер ететін күштер потенциалдық болса,
 (18.20)
(18.20)
(18.8) формулаға сәйкес:

Сол үшін (18.20) ны төмендегідей түрде жазу мүмкін:
 (18.21)
(18.21)
(18.17) мен (18.21) ді салыстырсақ :

Немесе
 (18.22)
(18.22)
келіп шығады.
Бірақ жүйе потенцалдық энергиясы 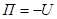 болғандығы себепті Ортақталған күш потенциалдық энергия арқылы төмендегідей өрнектеледі:
болғандығы себепті Ортақталған күш потенциалдық энергия арқылы төмендегідей өрнектеледі:
 (18.23)
(18.23)
5. Қозғалу мүмкіншілік принципі
Қозғалу мұмкіншілік принципі принципі механикалық жүйенің тепе-теңдігінің қажетті және жеткілікті шарттарын анықтайды.
Теорема. Идеал, босатпайтын, стационар байланыстар қойылған жүйе өзінің тепе-теңдік күйін сақтау үшін жүйеның кез-келген мүмкін болған өте кіші орын ауыстыруында оған қойылған актив күштердің атқарған жұмыстарының қосындысы нөлге тең болуы қажетті және жеткілікті. Қозғалу мұмкіншілік принципі принципінің математикалық өрнегі:
 (18.27)
(18.27)
(18.27) шарттың қажеттілігін дәлелдейік. Жүйе тепе-теңдік күйін сақтағандығы үшін оның әрбір  нүктесіне әсер етуші актив күштер және реакция күштерінің геометрик қосындысы нөлге тең болады:
нүктесіне әсер етуші актив күштер және реакция күштерінің геометрик қосындысы нөлге тең болады:
 (18.28)
(18.28)
Енді жүйеның әрбір нүктесіне 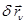 Қозғалу мұмкіншілік принципі береміз.
Қозғалу мұмкіншілік принципі береміз.
(18.28) ді 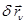 ге скаляр көбейтіп, кейін олардың қосындысын алсақ
ге скаляр көбейтіп, кейін олардың қосындысын алсақ

келіп шығады.
Байланыс идеал болғандықтан
 .
.
Нәтижеде

болады. Демек, (18.27) -теңдеудің қажеттілігі дәлелденді. Енді (18.27) шарттың жеткілікті екенін дәлелдейік. Бұл үшін (18.27) - шарт орындалғанымен жүйе тепе-тепеңдікте болмасын дейік. Бұл жағдайда жүйеның  нүктелері қозғалыста болады. Нәтижеде бұл нүктелерге әсер етуші күштердің тең әсер етушісі нөлге тең болмайды. Бастапқы кезде жүйе өзінің тыныштық күйін сақтағаны үшін оны құраушы
нүктелері қозғалыста болады. Нәтижеде бұл нүктелерге әсер етуші күштердің тең әсер етушісі нөлге тең болмайды. Бастапқы кезде жүйе өзінің тыныштық күйін сақтағаны үшін оны құраушы  нүктелері әсер етуші күштерден сәйкес
нүктелері әсер етуші күштерден сәйкес 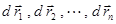 нақты өздерінің көшулерін алады. Жүйеға қойылған байланыс стационар болғаны себепті
нақты өздерінің көшулерін алады. Жүйеға қойылған байланыс стационар болғаны себепті  нақты көшулер
нақты көшулер  мүмкін болған көшулермен дәлме-дәл түседі.
мүмкін болған көшулермен дәлме-дәл түседі.
Бұл жағдайда:

Бұларды қоссақ,

келіп шығады.
Байланыс идеал болғандықтан
 .
.
Нәтижеде

табылады. Бұл біздің қойған шартымыздың дұрыс еместігін көрсетеді. Демек, жүйе өзінің тыныштық күйін сақтайды.
Қозғалу мұмкіншілік принципі принципін Лагранж ашқан. Сондықтан да бұл
принцип Лагранж принципі делінеді.
Қозғалу мұмкіншілік принципі принципінің аналитикалық өрнегі төмендегідей түрде жазылады:
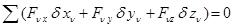 .
.
4. динамиканың жалпы теңдеуі
Динамиканың жалпы теңдеуін келтіріп шығару үшін идеал және босатпайтын байланыстағы механикалық жүйе нүктелері үшін Даламбер принципін жазамыз:
 (18.29)
(18.29)
Жүйе нүктелеріне мүмкін болатын көшулер беріп (18.29) теңдеулерді сәйкес  терге скаляр көбейтіп, алынған өрнектерді мүшелеп қоссақ,
терге скаляр көбейтіп, алынған өрнектерді мүшелеп қоссақ,
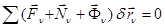
келіп шығады. Жүйе идеал байланыста болғандықтан
 .
.
Сонымен,
 (18.30)
(18.30)
өрнекке ие боламыз.
(20.2) теңдеу аналитикалық тәсілде Декарт координат өстеріндегі проекциялары арқылы төмендегідей жазылады:
 (18.31)
(18.31)
(18.30) немесе (18.31) динамиканың жалпы теңдеуі делінеді және келесі теоремамен баяндалады:
Идеал және босатпайтын байланыстар қойылған механикалық жүйеге әсер ететін актив күштердің және инерция күштерінің әр қандай мүмкін болатын көшудегі элементтер жұмыстарының қосындысы нөлге тең.
Динамиканың жалпы теңдеуі Даламбер және Лагранж принциптерін бірге қарастырудан келіп шыққандығы себепті, (18.30) Даламбер- Лагранж теңдеуі деп те аталады.
Дата добавления: 2019-02-22; просмотров: 893; Мы поможем в написании вашей работы! |

Мы поможем в написании ваших работ!
