Геометрические построения на чертежах.

⇐ ПредыдущаяСтр 4 из 4

Для того чтобы построить чертёж детали, провести плоскостную разметку для изготовления или обработки детали, необходимо выполнить ряд геометрических построений.

Геометрическим построением называют способ решения задачи, при котором все действия производятся чертёжными или разметочными инструментами.

Рассмотрим деление окружности графическим построением на равные части.

Деление окружности на три равные части.

Из точки О пересечения центровой линии с окружностью (рисунок 27) делают на окружности две засечки радиусом R, равным радиусу окружности. Полученные точки пересечения засечек с окружностью и точка О₁, противоположная точке О, делят окружность на три равные части.

Рисунок 27. Деление окружности на три равные части.

Деление окружности на пять равных частей.

Из точки О делают засечку на окружности радиусом окружности R (рисунок 28). Из точки пересечения засечки и окружности опускают перпендикуляр на центровую линию. Полученная точка О₁ является серединой радиуса окружности. Из точки О₁ радиусом R₁, делают засечку на диаметре. Радиус R₂равен одной пятой части окружности. Сделав радиусом R₂ засечки на окружности, получают точки деления окружности на пять равных частей.

Рисунок 28. Деление окружности на пять равных частей.

Деление окружности на шесть равных частей.

Сторона правильного шестиугольника, вписанного в окружность равна радиусу окружности.

Для деления окружности на шесть равных частей надо из точек О и О₁ пересечения центровой линии с окружностью сделать на окружности по две засечки радиусом R, равным радиусу окружности (рисунок 29). Соединив полученные точки отрезками прямых, получим правильный шестиугольник.

Рисунок 29. Деление окружности на шесть равных частей.

Деление окружности на семь равных частей.

Для того, чтобы разделить окружность на семь равных частей, из точки О делают засечку на окружности радиусом окружности R (рисунок 30). Из точки А пересечения засечки и окружности опускают перпендикуляр на центровую линию. Длина построенного перпендикуляра АВ равна стороне вписанного в данную окружность правильного семиугольника. Сделав засечки радиусом АВ, получают точки деления окружности на семь частей.

Рисунок 30. Деление окружности на семь равных частей.

Проецирование. Основные виды и их расположение на чертеже

Основным методом изображения предметов на чертеже является проекция (от латинского projectio – бросание вперёд, вдаль).

Основные элементы и сущность метода проецирования рассмотрим на примере точки (рисунок 31):

· плоскость проекций П’ – плоскость, на которую производится проецирование;

· центр проецирования S – точка из которой производится проецирование;

· точки А, В - объекты проецирования;

· проецирующие лучи SA и SB – воображаемые прямые, при помощи которых производится проецирование.

Рисунок 31. Метод проецирования.

Проведя через центр проекций S и точку А прямую линию до пересечения с плоскостью П’ получим точку А’. Точка А’ – проекция точки А на плоскость П’. Символически это .

Проведя через центр проекций S и точку В прямую линию до пересечения с плоскостью П’ получим точку В’. Точка В’ – проекция точки В на плоскость П’. Символически это .

Если центр проекций S находится на конечном расстоянии (т.е. все лучи проекций выходят из неё), то проецирование называется центральным.

Если центр проекций S бесконечно удалённая точка, то в обозримом пространстве проецирующие лучи будут параллельны. В этом случае проецирование называется параллельным (рисунок 32).

Если проецирующие прямые перпендикулярны плоскости проекций, то проецирование называют ортогональным или прямоугольным (рисунок 33).

Если проецирующие лучи не перпендикулярны к плоскости проекций, то проецирование называют косоугольным.

В процессе проецирования происходит изменение фигуры, которую проецируют, она теряет свои свойства и приобретает новые. Некоторые свойства остаются неизменными:

1. Проекция точки есть точка.

2. Если одна фигура принадлежит другой фигуре, то проекция первой фигуры принадлежит проекции второй фигуры.

Рисунок 32. Параллельное Рисунок 33. Ортогональное

проецирование проецирование

3. Если фигура принадлежит плоскости, параллельной плоскости проекций, то проекция фигуры на эту плоскость проекций равна самой фигуре, т.е. в натуральную величину.

Чертёж, состоящий из проекций объекта, называют комплексным чертежом. Для получения комплексного чертежа пользуются следующим алгоритмом:

1. Объект проецируют ортогонально на три взаимно перпендикулярные плоскости (рисунок 34).

2. Эти плоскости совмещают в одну путём поворота вокруг линии пересечения этих плоскостей (рисунок 35).

Для построения третьей проекции по двум данным необходимо выполнить следующее:

1. Через фронтальную проекцию А₂ провести перпендикуляр к оси z.

2. На проведённом перпендикуляре от оси z отложить отрезок равный расстоянию от горизонтальной проекции А₁ до оси х.

Рисунок 34. Проецирование точки на три плоскости проекций.

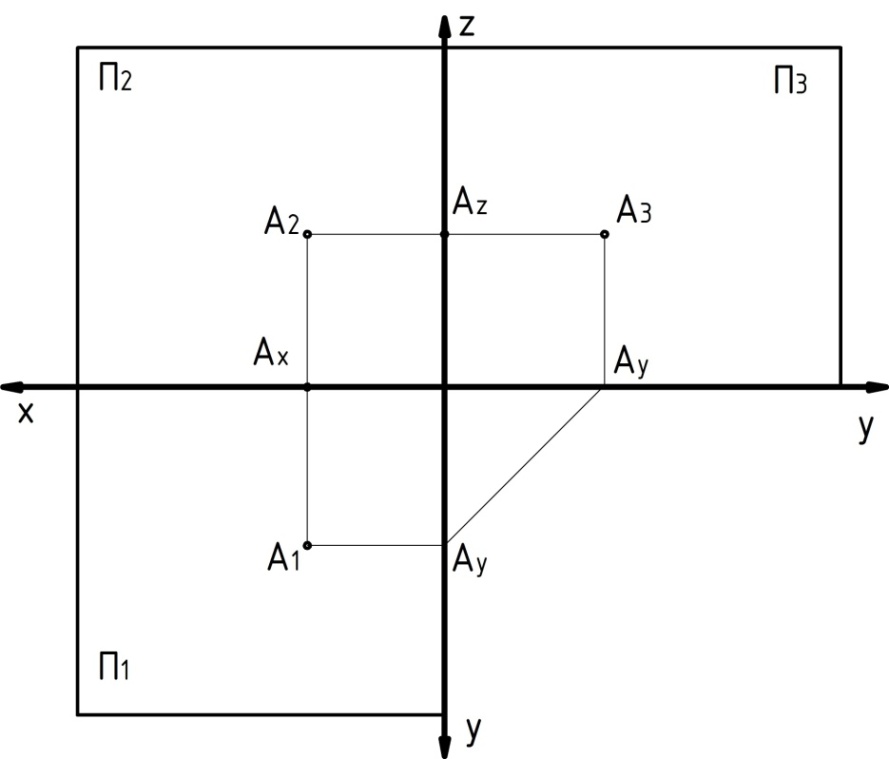
Рисунок 35. Комплексный чертёж точки.

При выполнении машиностроительных чертежей пользуются правилами прямоугольного проецирования. Предмет проецируют на 6 граней пустотелого куба, располагая его между наблюдателем и соответствующей гранью куба. Грани куба принимаются за основные плоскости проекций. Следовательно, имеется 6 основных плоскостей проекций (рисунок 36). Эти плоскости совмещаются разворотом в одну плоскость вместе с полученными на них изображениями.

Изображение на фронтальной плоскости проекций на чертеже принимается за главное. Предмет располагают так, чтобы изображение на фронтальной плоскости давало наиболее полное представление о форме и размерах предмета.

В инженерной графике изображения предметов называют видами.

Вид – изображение, обращённой к наблюдателю видимой части поверхности предмета.

В целях уменьшения количества изображений допускается показывать на видах невидимые контуры предмета штриховыми линиями.

Все виды на чертеже должны располагаться в проекционной связи. Это облегчает чтение чертежей. В этом случае не наносятся какие-либо надписи, разъясняющие наименование видов. Количество видов на чертеже должно быть наименьшим, но обеспечивающим полное представление о предмете.

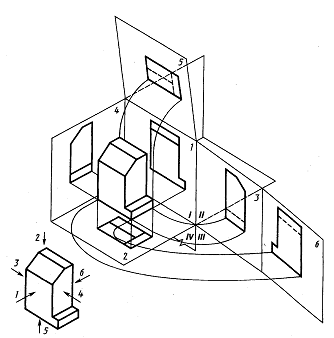
Рисунок 36. Образование основных видов.

По ГОСТ 2.305 – 68 устанавливаются следующие названия видов (рисунок 36):

1- Вид спереди (главный вид);

2- Вид сверху;

3- Вид слева;

4- Вид справа;

5- Вид снизу;

6- Вид сзади.

Рисунок 37. Расположение основных видов на чертеже.

Аксонометрические проекции.

Кроме прямоугольных (ортогональных) проекций для изображения предмета на чертеже используют аксонометрические проекции.

Чертёж даёт чёткое представление о форме и размерах объекта, но в некоторых случаях требуется наглядное представление предмета.

В этих случаях дают дополнительно изображение этого предмета в аксонометрической проекции.

Способ аксонометрического проецирования заключается в том, что данный предмет вместе с осями координат, к которым этот предмет отнесен в пространстве, параллельно проецируется на некоторую плоскость (рисунок 38). Следовательно, аксонометрическая проекция – это проекция только на одну плоскость.

В зависимости от направления проецирования аксонометрические проекции делят на два вида:

Косоугольное проецирование – проецирование не перпендикулярно плоскости аксонометрических проекций;

Прямоугольное проецирование – проецирование перпендикулярное к плоскости аксонометрических проекций.

Рисунок 38. Аксонометрическое проецирование.

Отношения расстояний по осям в пространстве к полученным аксонометрическим проекциям этих расстояний: e_x/e = k; e_y/e = m; e_z/e = n.

k, m, n называют коэффициентами искажения по осям.

В зависимости от величины коэффициентов аксонометрию делят на три вида:

Изометрия: k = m = n;

Диметрия: k = m ≠ n (e_x = e_z ≠ e_y);

Триметрия: k ≠ m ≠ n.

Триметрия применяется очень редко.

ГОСТ 2.317 – 69 устанавливает правила построения аксонометрических проекций, применяемых на чертежах всех отраслей промышленности и строительства.

Диметрическая проекция.

Коэффициент искажения по оси у составляет 0,47, а по осям x и z – 0,94.

Принято диметрическую проекцию выполнять без искажения по осям x и z, т.е. равным 1, а по оси у - 0,5 (меньше в 2 раза).

Окружности в аксонометрии проецируются в эллипс. Большая ось эллипсов будет составлять 1,06d, d - диаметр окружности, а малая ось эллипса в плоскости xz – 0,95d, эллипсов в плоскостях xy и zy – 0,35d.

Рисунок 39. Диметрическая проекция.

Изометрическая проекция.

Коэффициенты искажения по всем осям равны 1. Большая ось эллипсов – 1,22d, меньшая ось эллипсов – 0, 71d, где d – диаметр окружности.

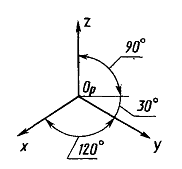
Рисунок 40. Изометрическая проекция.

ПРИЛОЖЕНИЕ

ГБПОУ «Курганский государственный колледж»

КОНТРОЛЬНАЯ РАБОТА

Специальность 08.02.01 Строительство и эксплуатация зданий и сооружений (заочное отделение)

Группа ЗС 102

Ф.И.О. студента Иванов И.И.

Вариант 0

По предмету: Инженерная графика

Преподаватель: Белошевская М.А.

Дата регистрации работы:

Оценка преподавателя:

Курган 2016

2016

Белошевская М.А.

Рисунок 1. Пример выполнения задания №1 «Титульный лист»

Белошевская М.А.

Рисунок 2. Пример выполнения задания №2 «Линии чертежа»

Белошевская М.А.

Рисунок 3. Пример выполнения задания №3 «Геометрические построения»

Белошевская М.А.

Рисунок 4. Пример выполнения задания 4 «Проекции детали», лист 1

Белошевская М.А.

Рисунок 5. Пример выполнения задания 4 «Проекции детали», лист 2.

Список литературы:

1. Боголюбов С.К. Инженерная графика. – М.: Машиностроение, 2000.

2. Куликов В.П., Кузин А.В. Инженерная графика: учебник – 3-е издание, испр. – М.:ФОРУМ, 2009.-368 с.- (Профессиональное образование).

3. Чекмарёв, А.А., Осипов В.К. Справочник по машиностроительному черчению - М.: Высшая школа, 2001г- 360с.

4. Чумаченко Г.В. Техническое черчение: учеб. пособ. для профессиональных училищ и технических лицеев / Г.В. Чумаченко, канд. тех. наук. –Изд. 6-е, стер. – Ростов н/Д : Феникс, 2013. -349 с. – (НПО).

5. alldrawings. ru.

5. cherch. ru.

6. nacherchy. ru.

7. Боголюбов С.К. Инженерная графика. – М.: Машиностроение, 2000.

8. Белягин, С.Н. Черчение: справ. пособие/ С.Н. Белягин. – 4-е изд., доп. – М.: ООО « Издательство АСТ»: ООО «Издательство Астрель», 2002-424с.

9. Государственные стандарты. Единая система конструкторской документации.

10. Вышнепольский, И.С. Техническое черчение: учеб. для студ. среднего проф. Образования / И.С. Вышнепольский. – М.: Высшая школа, 2001. – 392 с.

11. Миронов Б.Г., Сборник заданий по инженерной графике с примерами выполнения чережей на компьютере: Учеб. пособие / Б.Г Миронов, Р.С. Миронова, Д.А. Пятника, А.А. Пузиков – 3-е изд., испр. и доп. – М.: Высш. шк., 2003.-355с.

12. Степакова В.В., Гордиенко Н.А. Черчение. – М.: ООО «Издательство Астрель», 2004 – 272 с.

13. Чекмарёв А.А., Осипов В.К., Справочник по машиностроительному черчению – М.: Высшая школа, 2001г – 360с.

Дата добавления: 2019-02-22; просмотров: 848; Мы поможем в написании вашей работы!

Поделиться с друзьями:

⇐ Предыдущая 1 2 34

Мы поможем в написании ваших работ!