Адаптивные полиномиальные модели
Экспоненциальное сглаживание
Для экспоненциального сглаживания ряда используется рекуррентная формула
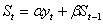 (5.1.),
(5.1.),
где 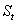 - значение экспоненциальной средней в момент t;
- значение экспоненциальной средней в момент t;
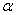 - параметр сглаживания,
- параметр сглаживания, 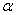 =сonst, 0<
=сonst, 0< 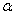 <1;
<1;
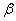 = 1-
= 1- 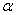 .
.
Если последовательно использовать соотношение (5.1.), то экспоненциальную среднюю 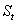 можно выразить через предшествующие значения уровней временного ряда. При n®¥
можно выразить через предшествующие значения уровней временного ряда. При n®¥
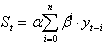 (5.2.)
(5.2.)
Таким образом, величина 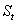 оказывается взвешенной суммой всех членов ряда. Причем веса отдельных уровней ряда убывают по мере их удаления в прошлое соответственно экспоненциальной функции (в зависимости от "возраста" наблюдений). Именно поэтому величина названа экспоненциальной средней.
оказывается взвешенной суммой всех членов ряда. Причем веса отдельных уровней ряда убывают по мере их удаления в прошлое соответственно экспоненциальной функции (в зависимости от "возраста" наблюдений). Именно поэтому величина названа экспоненциальной средней.
Например, пусть 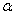 =0,3. Тогда вес текущего наблюдения
=0,3. Тогда вес текущего наблюдения 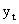 будет равен
будет равен 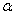 =0,3, вес предыдущего уровня
=0,3, вес предыдущего уровня 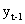 будет соответствовать
будет соответствовать 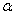 ´
´ 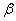 =0,3´0,7=0,21; для уровня
=0,3´0,7=0,21; для уровня 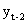 вес составит
вес составит 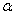 ´
´ 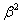 =0,147; для yt-3 вес
=0,147; для yt-3 вес 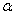 ´
´ 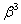 =0,1029 и т.д.
=0,1029 и т.д.
Предположим, что модель временного ряда имеет вид:
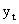 =
= 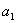 +
+ 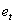 .
.
Английский математик Р. Браун показал, что математические ожидания ряда и экспоненциальной средней совпадут, но в то же время дисперсия экспоненциальной средней D[ 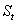 ] меньше дисперсии временного ряда (
] меньше дисперсии временного ряда ( 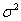 )
)
 (5.3.)
(5.3.)
Из (5.3.) видно, что при высоком значении 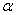 дисперсия экспоненциальной средней незначительно отличается от дисперсии ряда. С уменьшением
дисперсия экспоненциальной средней незначительно отличается от дисперсии ряда. С уменьшением 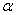 дисперсия экспоненциальной средней сокращается, возрастает ее отличие от дисперсии ряда. Тем самым, экспоненциальная средняя начинает играть роль «фильтра», поглощающего колебания временного ряда.
дисперсия экспоненциальной средней сокращается, возрастает ее отличие от дисперсии ряда. Тем самым, экспоненциальная средняя начинает играть роль «фильтра», поглощающего колебания временного ряда.
|
|
|
Таким образом, с одной стороны, следует увеличивать вес более свежих наблюдений, что может быть достигнуто повышением 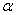 (согласно(5.2.)), с другой стороны, для сглаживания случайных отклонений величину
(согласно(5.2.)), с другой стороны, для сглаживания случайных отклонений величину 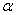 нужно уменьшить. Эти два требования находятся в противоречии. Поиск компромиссного значения параметра сглаживания
нужно уменьшить. Эти два требования находятся в противоречии. Поиск компромиссного значения параметра сглаживания 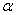 составляет задачу оптимизации модели.
составляет задачу оптимизации модели.
Иногда поиск этого значения параметра осуществляется путем перебора. В этом случае в качестве оптимального выбирается то значение 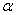 , при котором получена наименьшая дисперсия ошибки. Например, при построении этих моделей с помощью пакета "Мезозавр" в меню предусмотрена ветвь "оптимизация", реализующая поиск значения по этой схеме.
, при котором получена наименьшая дисперсия ошибки. Например, при построении этих моделей с помощью пакета "Мезозавр" в меню предусмотрена ветвь "оптимизация", реализующая поиск значения по этой схеме.
При использовании экспоненциальной средней для краткосрочного прогнозирования предполагается, что модель ряда имеет вид:
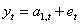 ,
,
где 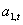 - варьирующий во времени средний уровень ряда,
- варьирующий во времени средний уровень ряда,
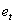 - случайные неавтокоррелированные отклонения с нулевым математическим ожиданием и дисперсией
- случайные неавтокоррелированные отклонения с нулевым математическим ожиданием и дисперсией 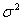 .
.
Прогнозная модель определяется равенством:
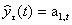 ,
,
где 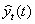 - прогноз, сделанный в момент t на
- прогноз, сделанный в момент t на 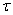 единиц времени (шагов) вперед;
единиц времени (шагов) вперед;
|
|
|
â 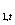 - оценка â
- оценка â 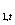 (знак ^ над величиной означает оценку).
(знак ^ над величиной означает оценку).
Единственный параметр модели â 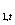 определяется экспоненциальной средней:
определяется экспоненциальной средней:
â 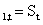
â 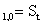
Выражение (5.1.) можно представить по-другому, перегруппировав члены:
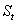 =
= 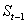 +
+ 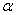 (
( 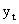 -
- 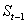 ) (5.4.)
) (5.4.)
Величину ( 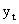 -
- 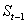 ) можно рассматривать как погрешность прогноза. Тогда новый прогноз
) можно рассматривать как погрешность прогноза. Тогда новый прогноз 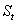 получается в результате корректировки предыдущего прогноза с учетом его ошибки. В этом и состоит адаптация модели.
получается в результате корректировки предыдущего прогноза с учетом его ошибки. В этом и состоит адаптация модели.
Экспоненциальное сглаживание является примером простейшей самообучающейся модели. Вычисления чрезвычайно просты, выполняются итеративно, причем массив прошлой информации уменьшен до единственного значения 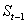 .
.
Адаптивные полиномиальные модели
Понятие экспоненциальной средней можно обобщить в случае экспоненциальных средних более высоких порядков.
Выравнивание p-го порядка:
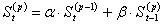 (5.5.)
(5.5.)
является простым экспоненциальным сглаживанием, примененным к результатам сглаживания (р-1)-го порядка.
Если предполагается, что тренд некоторого процесса может быть описан полиномом степени n, то коэффициенты предсказывающего полинома могут быть вычислены через экспоненциальные средние соответствующих порядков.
|
|
|
В случае, когда исследуемый процесс, состоящий из детерминированной и случайной компоненты, описывается полиномом n-го порядка, прогноз на 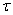 шагов вперед осуществляется по формуле:
шагов вперед осуществляется по формуле:
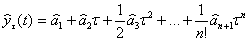 (5.6.),
(5.6.),
где 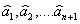 - оценки параметров.
- оценки параметров.
Фундаментальная теорема метода экспоненциального сглаживания и прогнозирования, впервые доказанная Р. Брауном и Р. Майером, говорит о том, что (n+1) неизвестных коэффициентов полинома n-го порядка 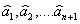 могут быть оценены с помощью линейных комбинаций экспоненциальных средних
могут быть оценены с помощью линейных комбинаций экспоненциальных средних 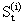 , где i=1¸n+1.
, где i=1¸n+1.
Следовательно, задача сводится к вычислению экспоненциальных средних, порядок которых изменяется от 1 до n+1, а затем через их линейные комбинации - к определению коэффициентов полинома.
На практике обычно используются полиномы не выше второго порядка. Например, при использовании полинома первого порядка адаптивная модель временного ряда имеет вид:
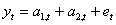 (5.7.),
(5.7.),
где 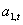 - значение текущего t-го уровня;
- значение текущего t-го уровня;
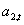 - значение текущего прироста.
- значение текущего прироста.
В таблице (5.1.) приведены формулы, необходимые для расчета по этим моделям.
Процедура прогнозирования временных рядов по методу экспоненциального сглаживания сравнительно проста и состоит из следующих этапов:
1. Выбирается вид модели экспоненциального сглаживания, задается значение параметра сглаживания 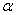 . При выборе порядка адаптивной полиномиальной модели могут использоваться различные подходы, например, графический анализ, метод изменения разностей и др.
. При выборе порядка адаптивной полиномиальной модели могут использоваться различные подходы, например, графический анализ, метод изменения разностей и др.
|
|
|
2. Определяются начальные условия. Например, для полиномиальной модели первого порядка необходимо определить 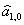 ;
; 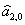 . Чаще всего в качестве этих оценок берут коэффициенты соответствующих полиномов, полученные методом наименьших квадратов. Начальные условия для модели нулевого порядка обычно получают усреднением нескольких первых уравнений ряда. Зная эти оценки, с помощью указанных в таблице формул находят начальные значения экспоненциальных средних.
. Чаще всего в качестве этих оценок берут коэффициенты соответствующих полиномов, полученные методом наименьших квадратов. Начальные условия для модели нулевого порядка обычно получают усреднением нескольких первых уравнений ряда. Зная эти оценки, с помощью указанных в таблице формул находят начальные значения экспоненциальных средних.
3. Производится расчет значений соответствующих экспоненциальных средних.
4. Находятся оценки коэффициентов модели.
5. Осуществляется прогноз на одну точку вперед, находится отклонение фактического значения временного ряда от прогнозируемого. Шаги с 3 по 5 данной процедуры повторяются для всех t£n , где n- длина ряда.
6. Окончательная прогнозная модель формируется на последнем шаге в момент t=n. Прогноз получается на базе выражения (5.6.) путем подстановки в него последних значений коэффициентов и времени упреждения 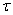 .
.
К положительным особенностям рассмотренных моделей следует отнести то, что при поступлении новой, свежей информации расчеты повторять не придется. Достаточно принять в качестве начальных условий последние значения функций сглаживания 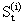 и продолжить вычисления.
и продолжить вычисления.
Таблица 5.1.
Дата добавления: 2019-02-22; просмотров: 738; Мы поможем в написании вашей работы! |

Мы поможем в написании ваших работ!
