Связь между коэффициентами регрессии и корреляции
Между коэффициентом корреляции и параметром парной линейной регрессии существует зависимость, которая применительно к выборочным оценкам может быть представлена следующим образом:
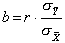,(2.7)
где: и sy, sx – средние квадратические ошибки.
Приведенное выражение позволяет оценить параметр регрессии без решения системы нормальных уравнений при условии, что коэффициент корреляции уже определен. На основе формулы (9.7) легко показать, что выборочный коэффициент корреляции равен среднему геометрическому выборочных коэффициентов регрессии. Действительно, Сравнив формулы (9.3) с основной формулой (8.1) коэффициента корреляции, видим, что их числители равны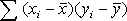 
. Это свидетельствует об определенной связи между этими характеристиками. Выборочный коэффициент корреляции выражается тогда равенством r2 = by/x * bx/y , откуда
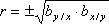. (2.8)
Эта формула ценна тем, что, во-первых, может быть использована для нахождения неизвестной величины коэффициента корреляции по известным значениям коэффициента регрессии by/x и bx/y, а во-вторых, позволяет контролировать правильность расчета коэффициента корреляции, если известны величины by/x и bx/y. Знак выборочного коэффициента корреляции совпадает со знаком выборочных коэффициентов регрессии, что следует из формулы (9.3). Если зависимость между признаками функциональная, то by/x = 1 / bx/y и, следовательно, r = 1. И, наоборот, при полном отсутствии взаимосвязи между признаками by/x= 0, bx/y= 0, и r = 0.
|
|
|
Определение параметров парной линейной регрессии
Определение параметров линейной регрессии – одна из задач регрессионного анализа. Она решается способом наименьших квадратов, основанным на требовании, чтобы сумма квадратов отклонений вариант от линии регрессии была наименьшей. Этому требованию удовлетворяет следующая система нормальных уравнений:
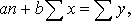
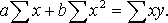
Ряды регрессии — это ряды усредненных значений (yx и xy) варьирующих признаков Y и X, соответствующих значениям аргументов xi и yi. Поэтому эмпирические уравнения регрессии следует записывать так:
yx = ay/x + by/x*x
и xy = ax/y + bx/y*y (2.9)
Формулы для определения параметров а и b принимают следующие выражения:
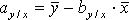
и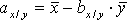 
. (2.10)
Уравнение линейной регрессии можно выразить в виде отклонений вариант от их средних арифметических:
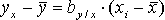
и 
. (2.11)
В таком случае система нормальных уравнений для определения параметров а и b будет следующая:
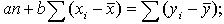
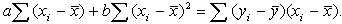
Поскольку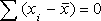 
и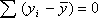 
, то параметр b выразится в виде приведенной формулы (2.3); параметр а легко найти по формуле (2.4).
Если средние 
и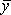 
перенести в правую часть уравнения (2.11), то при 
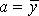система нормальных уравнений принимает следующий вид:
|
|
|
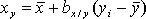
и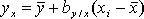 
, (2.12)
Заменив в формуле (2.11) параметры by/x и bx/y на их значения из формулы (2.3), получим систему уравнений парной линейной регрессии:
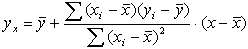
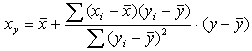. (2.13)
Эти уравнения удобны для определения параметров при отыскивании эмпирических уравнений регрессии в практической работе для точности прогнозирования результатов.
Дата добавления: 2019-02-12; просмотров: 530; Мы поможем в написании вашей работы! |
Мы поможем в написании ваших работ!